🔑 Key Point
- 결정트리 학습 알고리즘
- Bagging 원리
- Random Forest의 랜덤성이 과적합 해소에 미치는 영향
1. 트리기반 모델
선형회귀모델은 특성과 타겟의 관계가 선형적이라고 가정하고, 비용함수를 최소로 하는 파라미터를 찾는 모델이었다. 그렇다면 관계가 비선형적인 경우에는 어떻게 하냐? 이때 사용하는게 트리기반 모델(tree-based model)
* 결정트리(Decision Tree)
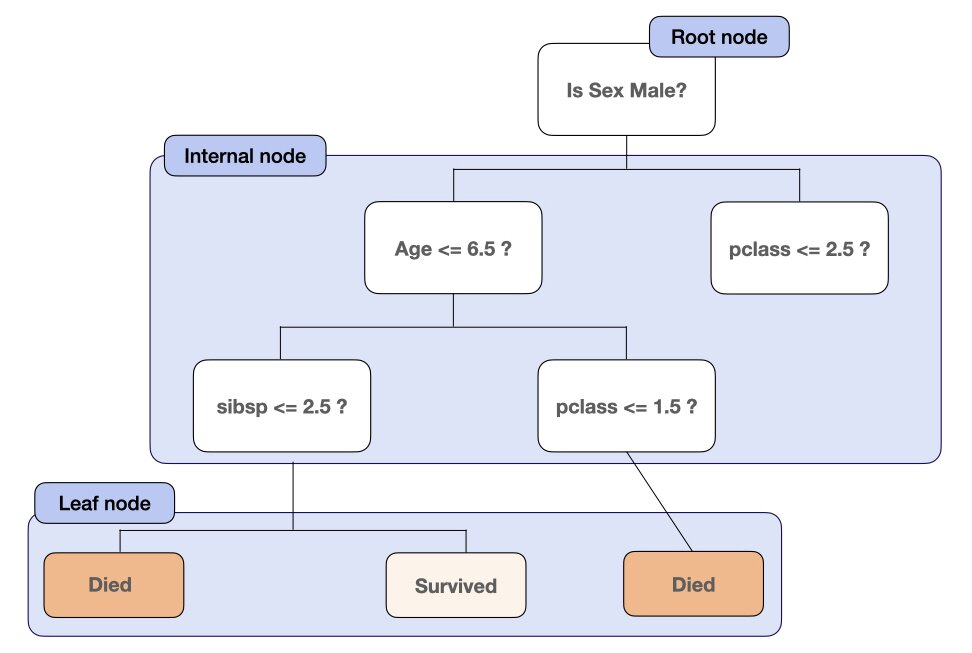
결정트리는 비용함수를 최소로 하는 특성과 그 값에 대한 Yes/No의 대답으로 타겟 데이터를 분류한다.
노드와 선인 엣지로 이루어져있다. 처음으로 분기되는 노드는 루트노드, 중간은 인터널 노드, 더이상 분기되지 않는 노드는 리프라고 한다.
| 장점 | 데이터 분할과정이 직관적, 시각화 가능해 이해하고 해석하기 용이 데이터 전처리 과정이 많이 필요 X 특성간 상호작용 포착 가능 다중 출력 문제 풀 수 있음 |
| 단점 | 훈련데이터에 대한 제약사항이 거의 없어서 과적합될 위험 한개의 트리만을 사용하기 때문에 한 노드에서 생긴 에러가 하부 노드에 계속 영향을 줌 각각의 분기에선 최적이지만, 전체로 봤을땐 최적인 의사결정트리 보장X (탐욕알고리즘 사용) 근사치를 예측값으로 반환 → 외삽 어려움 |
결정트리는 회귀, 분류 문제에 모두 적용할 수 있다.회귀에서 비용함수는 MSE이고, 마지막 노드에 있는 타겟값들의 평균을 예측값으로 반환, 분류에서 비용함수는 불순도이며 최빈값을 예측값으로 반환한다.
* 불순도(impurity) → 지니불순도, 엔트로피
여러개가 섞여있는 정도. 타겟 데이터를 분할하는 특성과 분할하는 지점을 찾아내는 기준
- 지니불순도(Gini Impurity or Gini Index)
- 범주는 0~0.5 사이
- 6:4와 8:2로 혼합되어있다면 6:4가 불순도가 더 높음
- 불순도가 낮으면 순수도는 높음
- 엔트로피(Entropy)
- 범주는 0~1 사이
- 엔트로피를 사용하여 정보획득량을 구할 수 있음
- 불순도를 감소시킬수록 중요한 변수로 취급 → 가장 우선적으로 자주 사용
- 정보획득(Information Gain)은 특정한 특성을 사용해 분할했을 때 엔트로피의 감소량을 뜻함
- 정보획득 = 분할 전 노드 불순도 - 분할 후 자식노드들의 불순도
2. 파이프 라인(Pipeline)
머신러닝에서 파이프라인을 사용해서 모델학습을 쉽게 해준다.
- 편의성과 캡슐화 (fit, predict 한번 사용으로 전체 모델 과정 수행 가능)
- 하이퍼파라미터 선택
- 안전성
pipe_dt = make_pipeline(
OrdinalEncoder(),
SimpleImputer(),
DecisionTreeClassifier(random_state=1, criterion="entropy"),
)
pipe_dt.fit(X_train, y_train)과적합 해소하기 위해서는 하이퍼 파라미터 조정해준다. 공식문서
- min_samples_split
- min_samples_leaf
- max_depth
3. 랜덤포레스트(RandomForest)
결정트리의 단점인 과적합과 불안정성을 해결하기 위해 랜덤포레스트를 사용
앙상블 기법 중 배깅-bagging을 대표하는 모델 중 하나
앙상블 : 여러 모델들의 결과를 참고하여 최종 타겟값을 결정하는 기법(ex.배깅, 부스팅)배깅 : 랜덤복원추출을 사용하여 기본 모델들을 만든 후에 각각의 기본 결과를 회귀에서는 평균, 분류에서는 다수결의 방법을 사용하여 최종 타겟값을 결정
앙상블에 사용하는 기본 모델들은 부트스트래핑 샘플링 과정으로 얻은 세트를 통해 학습함
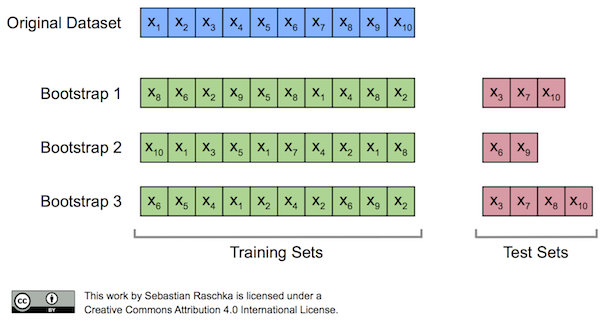
* Out-of Bag Samples(oob sample)
oob sample은 부트스트랩 과정에서 한번도 추출되지 않은 샘플을 의미
* Aggregation
부트스트랩세트로 만들어진 기본모델들을 합치는 과정
회귀문제일 경우 기본모델 결과들의 평균으로 예측값을 내고,
분류문제일 경우 다수결로 가장 많은 모델들이 선택한 범주로 예측
랜덤포레스트의 경우에도 과적합을 해소하기 위해 하이퍼파라미터를 조정해준다. 공식문서
- max_depth
- min_samples_split
- min_samples_leaf
<랜덤포레스트에만 있는 하이퍼파라미터>
- n_estimators : 기본 모델의 수
- max_features : 분할에 사용되는 최대 특성의 수
- oob_score : oob sample을 이용한 검증 스코어 반환 여부
<랜덤 포레스트 의사코드>

디스커션 내용 정리하기
RF :
의사결정나무, 랜덤포레스트를 이용한 분류
의사결정나무정보획득
엔트로피란?
공식문서
랜덤포레스트
트리모델 인코딩
