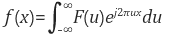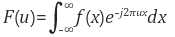푸리에 변환 (Fourier Transform)

매번 해야지 해야지... 해놓고서는 미뤄뒀던 푸리에... 늦게라도 공부해보려 한다.

푸리에 변환은 신호처리, 음성, 통신 분야에서 뿐만 아니라 영상처리에서도 굉장히 중요한 개념으로 다양한 응용을 가지고 있다. 영상을 주파수 성분으로 변환하여 다양한 분석 및 처리를 할 수 있고 임의의 필터링 연산 (FFT, fast Fourier transform)을 이용하여 고속으로 구현할 수 있다.

푸리에 변환을 실제 활용하는데 있어 필요한 사항들을 최대한 직관적으로 정리한 블로그를 참고하여 글을 작성한다.

푸리에에 본 블로그의 저자는 푸리에 변환을 통해 얻어지는 스펙트럼과 페이즈(phase)중 페이즈란 무엇인가? 그리고 푸리에 주파수 공간의 좌표값을 어떻게 해석할까?에 대해 고민한다. 이에 대한 해결책 역시 다룬다.

푸리에 변환(Fourier Transform) 이해

푸리에 변환의 개념적 이해

푸리에 변환을 직관적으로 설명하면 임의의 입력 신호를 다양한 주파수를 갖는 주기함수들의 합으로 분해하여 표현하는 것이다. (벌써 어렵다..)

좀더 자세히 말하면, 푸리에 변환에서 사용하는 주기함수는 sin, cos 삼각함수이며 푸리에 변환은 고주파부터 저주파까지 다양한 주파수 대역의 sin, cos 함수들로 원본 신호를 분해하는 것이다.
(※주파수: Hz 단위를 사용하는 1초당 진동 회수 (wave number))

아래 그림의 예를 보면, 맨 앞의 붉은 색 신호는 입력 신호이고 뒤의 파란색 신호들은 푸리에 변환을 통해 얻어진 주기함수 성분들이다. 각각의 주기함수 성분들은 고유의 주파수(frequency)와 강도(amplitude)를 갖고 있으며 이들을 모두 합치면 다시 붉은색의 원본 신호가 된다.

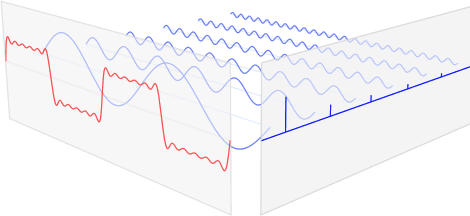
여기서 입력 신호는 전파, 음성 신호 등과 같이 시간축(time)에 대해 정의된 신호일 수도 있고 이미지(image)등과 같이 공간축에 대해 정의된 신호일 수 있다. 통신 분야에서는 푸리에 변환을 time domain에서 frequency domain으로의 변환이라고 하면, 컴퓨터 비전(computer vision), 영상처리 쪽에서는 spatial domain에서 frequency domain으로의 변환이라고 부른다. 결국 핵심은 입력 신호를 sin, cos 주기성분으로 분해한다는 것이다.

푸리에 변환의 수식적 이해

• 
• 

위 수식을(1), 아래 수식을 (2)라고 하자.

여기서 i는 허수단위 $i=\sqrt{-1}$, f(x)는 원본 입력 신호, $e^{i2\pi ux}$는 주파수 u인 주기함수 성분, F(u)는 해당 주기함수 성분의 계수(coefficient)를 나타낸다.

식을 그대로 해석하면 식(1)은 입력신호 f(x)가 $e^{i2\pi ux}$들의 합으로 표현(분해)된다 는 의미이다. 그리고 식(2)는 f(x)를 주기함수 성분으로 분해했을 때의 계수(coefficient) F(u)가 식(2)로 주어진다는 의미이다. 앞서 그림 1과 연관해보면 $e^{i2\pi ux}$는 f(x)를 구성하는 (파란색의 주파수 u인) 주기함수 성분들이고 F(u)는 해당 주기함수 성분의 강도(amplitude)를 나타낸다.

일반적인 푸리에 변환에 대한 설명은 식(2)를 푸리에 변환이라고 정의하고 식(1)을 푸리에 역변환(inverse Fourier Transform)이라고 정의한다. 그리고 푸리에 역변환을 함녀 다시 원래의 함수로 돌아온다고 한다.(그러나 이렇게만 얘기하면 사실 직관적인 이해가 되지 않고 그저 주입식 교육이 된다...)

그래서 더 자세히 들어가기 위해 $e^{i2\pi ux}$의 의미를 이해해보자. 그리고 이를 위해 오일러 공식(Euler's formula)이 필요하다.

---

※ 오일러 공식

오일러 공식은 복소지수함수를 삼각함수로 변환할 수 있도록 하는 유명한 식이다.

---

• 

위 식의 증명은 다른 곳을 통해 쉽게 알수 있다고 한다.. 이 식을 이용하면 (1)의 $e^{i2\pi ux}$는 실수부가 $cos(2\pi ux)$, 허수부가 $sin(2\pi ux)$인 주기함수임을 알 수 있다.

• 

여기서 $cos(2\pi ux)$, $sin(2\pi ux)$모두 주기(period)가 1/u, 주파수(frequency) u인 주기 함수이므로 결국 $e^{i2\pi ux}$는 주파수 u인 정현파의 복소지수함수 표현임을 알 수 있다.

• 주기: 파동이 한번 진동하는데 걸리는 시간, 또는 길이. sin(wx)의 주기는 $2\pi/w$
• 주파수: 1초 동안의 진동 횟수, 주파수와 주기는 서로 역수 관계 (주파수 = 1/주기)
• 정현파: 파형이 sin 또는 cos함수인 파동(wave)

핵심은 식 (1)은 함수 f(x)를 모든 가능한 주파수(u)의 주기함수들(ej2πux)의 일차결합으로 표현한 것이다. 그리고 그 일차결합 계수 F(u)는 식 (2)로 항상 주어질 수 있다는 것이 요지이다. 이와 같이 푸리에 변환식을 볼 수 있다면 푸리에 변환의 핵심을 이해한 것이다.

이후

비디오, 페이즈 등에 대한 자세한 설명 역시 이해하고 적어놓으면 좋겠지만, 일단 기본적인 개념이 어떻게 이뤄지는지는 이정도만으로 충분할 것 같다.(사실 뒤쪽은 좀 어려워 보여서 나중에 정리할 시간이 되면 해보는 걸루...) 더 자세한 내용은 참고 블로그를 통해서 확인해보자.

참고

• https://darkpgmr.tistory.com/171