세그먼트 트리를 사용하는 곳과 이유

• 구간 합을 구할 때 자주 사용한다.
• 구간 합을 구하기 위해서는 단순히 for 문을 사용하면 $O(N)$의 시간 복잡도가 나오지만 세그먼트 트리를 이용하면 $O(logN)$의 시간 복잡도를 가지기 때문에 더 빠른 처리가 가능하다.

세그먼트 트리

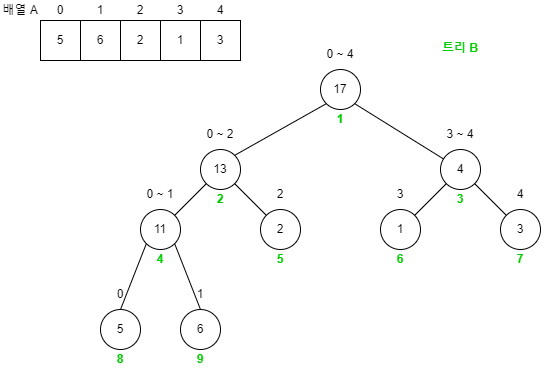
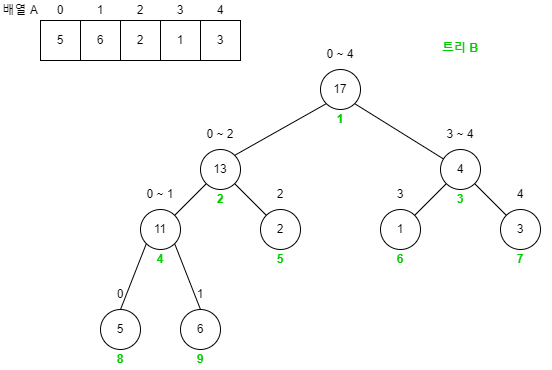
• 배열 A는 인덱스 0부터 시작한다.
• 트리 B는 인덱스 1부터 시작한다. 그 이유는 이렇게 할 경우 왼쪽 자식 노드의 인덱스는 부모 노드의 2배, 오른쪽 자식 노드의 인덱스는 부모 노드의 2배 + 1이 되기 대문이다.
• 노드 위에 쓰여 있는 값은 배열 A를 기준으로 합의 구간이다.

세그먼트 트리 초기화 방법

• 배열 A를 이용하여 세그먼트 트리 배열을 초기화해야한다. 이때 노드 번호가 트리 배열의 인덱스가 되며 다음과 같다.

int init(int start, int end, int node) {
	if (start == end) { //누적합 시작과 끝이 같을 때 == 누적합을 하지 않은 본연의 값
		tree[node] = A[start]; //해당 노드에 본연의 값을 저장
		return tree[node]; //해당 노드 값 리턴
	}
	int mid = (start + end) / 2; //시작과 끝 중간 값 구하기
	int left = init(start, mid, node * 2); //왼쪽 자식 노드는 start에서 mid까지 누적합이고 이때 노드의 인덱스는 부모 노드의 2배
	int right = init(mid + 1, end, node * 2 + 1); //오른쪽 자식 노드는 mid + 1에서 end까지 누적합이고 이때 노드의 인덱스는 부모 노드의 2배 + 1
	tree[node] = left + right; //해당 노드의 값은 왼쪽 자식 노드와 오른쪽 자식 노드의 합
	return tree[node]; // 해당 노드 값 리턴
}

• start == end인 경우는 누적합의 시작과 끝이 같다는 의미로 이는 곧 start만을 의미하여 tree[node]에 A[start]를 넣는다.
• mid는 시작과 끝의 중간 값으로 이를 통해서 왼쪽 자식 노드의 끝, 오른쪽 자식 노드의 시작을 표현할 수 있다.
• left는 왼쪽 자식 노드의 값으로 이는 왼쪽 자식 노드 까지의 구간 합이라고 볼 수 있다.
• right는 오른쪽 자식 노드의 값으로 이는 오른쪽 자식 노드까지의 구간 합이라고 볼 수 있다.
• 해당 노드의 값은 left와 right를 더한 값이 된다.
• 재귀적 방식으로 초기화한다.

세그먼트 트리에서 구간합 구하는 방법

int sum(int start, int end, int node, int left, int right) {
	//범위를 벗어나는 경우
	if (left > end || right < start) {
		return 0;
	}
	if (left <= start && end <= right) {
		//start와 end가 구하고 싶은 구간 내에 존재할 때
		//재귀적으로 들어갈 때 start가 left보다 커질수 있고 end가 right보다 작아질 수 있다.
		return tree[node]; //해당 노드 값 리턴
	}
	int mid = (start + end) / 2;
	//왼쪽에서 해당하는 범위 내의 모든 합과 오른쪽에서 해당하는 범위 내의 모든 합이 합쳐저 리턴
	return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right); 
}

세그먼트 트리에서 값을 업데이트 하는 방법

• 단순히 값을 업데이트하고 세그먼트 트리를 사용하면 $O(N)$의 시간복잡도가 갱신 될 때마다 발생한다.

void update(int start, int end, int node, int index, int value) {
	//index가 범위를 넘어가는 경우 리턴
	if (index > end || index < start) {
		return;
	}
	//해당 index가 저장되어 있는 노드를 찾은 경우
	if (start == end) {
		tree[node] = value; //해당 노드 값을 value로 바꿔준다.
		return; //리턴
	}
	int mid = (start + end) / 2; //시작 끝 중간 값 구하기
	if (mid < index) { //중간 값보다 index가 더 큰 경우 -> 오른쪽에 index가 있는 경우
		update(mid + 1, end, node * 2 + 1, index, value); //오른쪽 노드에서 다시 찾기
	}
	else {
		update(start, mid, node * 2, index, value); //왼쪽 노드에서 다시 찾기
	}
	tree[node] = tree[node * 2] + tree[node * 2 + 1];
}

1. 우선 해당 인덱스 번호에 해당하는 노드를 찾을 때까지 재귀적으로 들어가서 찾는다.
2. start == end인 경우 찾은 경우이며 이때 해당 노드 값을 업데이트한다.
3. 재귀적으로 빠져 나오면서 부모 노드의 값을 자식 노드들의 합으로 업데이트한다.

• 이렇게 하면 시간 복잡도가 $O(logN)$이 된다.

세그먼트 트리 예시 코드

#include <iostream>


using namespace std;

int A[10001] = { 0 };
int tree[100000] = { 0 };

int init(int start, int end, int node) {
	if (start == end) { //누적합 시작과 끝이 같을 때 == 누적합을 하지 않은 본연의 값
		tree[node] = A[start]; //해당 노드에 본연의 값을 저장
		return tree[node]; //해당 노드 값 리턴
	}
	int mid = (start + end) / 2; //시작과 끝 중간 값 구하기
	int left = init(start, mid, node * 2); //왼쪽 자식 노드는 start에서 mid까지 누적합이고 이때 노드의 인덱스는 부모 노드의 2배
	int right = init(mid + 1, end, node * 2 + 1); //오른쪽 자식 노드는 mid + 1에서 end까지 누적합이고 이때 노드의 인덱스는 부모 노드의 2배 + 1
	tree[node] = left + right; //해당 노드의 값은 왼쪽 자식 노드와 오른쪽 자식 노드의 합
	return tree[node]; // 해당 노드 값 리턴
}

int sum(int start, int end, int node, int left, int right) {
	//범위를 벗어나는 경우
	if (left > end || right < start) {
		return 0;
	}
	if (left <= start && end <= right) {
		//start와 end가 구하고 싶은 구간 내에 존재할 때
		//재귀적으로 들어갈 때 start가 left보다 커질수 있고 end가 right보다 작아질 수 있다.
		return tree[node]; //해당 노드 값 리턴
	}
	int mid = (start + end) / 2;
	//왼쪽에서 해당하는 범위 내의 모든 합과 오른쪽에서 해당하는 범위 내의 모든 합이 합쳐저 리턴
	return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right); 
}

void update(int start, int end, int node, int index, int value) {
	//index가 범위를 넘어가는 경우 리턴
	if (index > end || index < start) {
		return;
	}
	//해당 index가 저장되어 있는 노드를 찾은 경우
	if (start == end) {
		tree[node] = value; //해당 노드 값을 value로 바꿔준다.
		return; //리턴
	}
	int mid = (start + end) / 2; //시작 끝 중간 값 구하기
	if (mid < index) { //중간 값보다 index가 더 큰 경우 -> 오른쪽에 index가 있는 경우
		update(mid + 1, end, node * 2 + 1, index, value); //오른쪽 노드에서 다시 찾기
	}
	else {
		update(start, mid, node * 2, index, value); //왼쪽 노드에서 다시 찾기
	}
	tree[node] = tree[node * 2] + tree[node * 2 + 1];
}

int main() {
	int N;
	cin >> N; //입력 할 요소 개수
	for (int i = 0; i < N; i++) {
		int tmp;
		cin >> tmp;
		A[i] = tmp;
	}
	init(0, N - 1, 1); //초기화, node가 1인 이유는 tree의 경우 시작 노드 번호를 1로 한다.
	cout << sum(0, N - 1, 1, 2, 4) << endl; //인덱스 2-4의 구간합 출력
	update(0, N - 1, 1, 1, 4); //인덱스 1의 값을 4로 갱신
	cout << sum(0, N - 1, 1, 1, 4) << endl; //인덱스 1-4의 구간합 출력

	return 0;
}