Binary Search의 정의

• 문제를 둘로 쪼개서 답이 나올 수 있는 범위만 탐색하는 것

Binary Search의 특징

• 반드시 데이터가 정렬되어 있어야한다.

Divide and Conquer & Binary Search

분할 정복 알고리즘(Divide and Conquer)

• Divide : 문제를 하나 또는 둘 이상으로 나눈다.
• Conquer : 나눠진 문제가 충분히 작고, 해결이 가능하다면 해결하고, 그렇지 않다면 다시 나눈다.

이진 탐색(Binary Search)

• Divide : 리스트를 두 개의 서브 리스트로 나눈다.
• Conquer : 검색할 숫자가 중간 값보다 작다면 앞부분의 서브 리스트에서 검색할 숫자를 찾고 검색할 숫자가 중간 값보다 크다면 뒷부분의 서브 리스트에서 검색할 숫자를 찾는다.
• 재귀적으로 구현한다.

Binary Search 시간복잡도

• 처리할 때마다 탐색할 데이터가 $1 \over 2$씩 감소한다.
• $O(log_2n + 1)$의 시간 복잡도를 가진다.(1은 마지막 배열의 크기가 1일 때의 비교)

대표 예제

[백준] 1920번 수 찾기

📝 문제

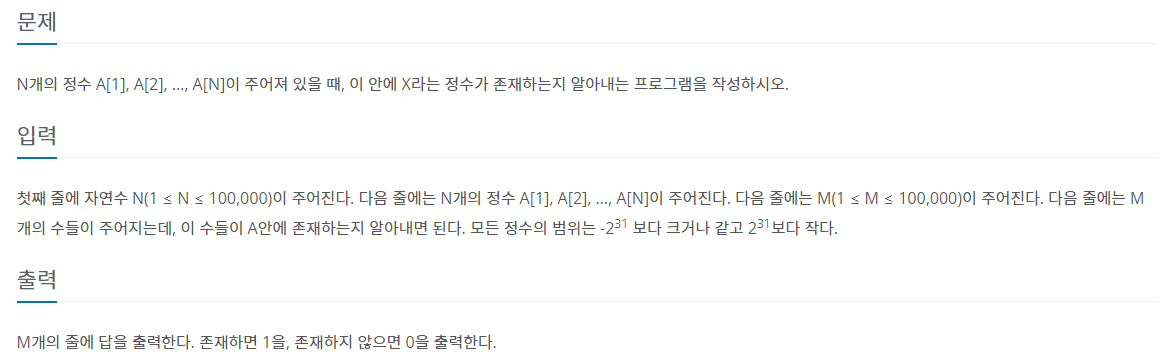
📌 풀이

1. 입력받은 배열을 정렬한다.
2. Binary Search를 이용하여 해결하며, 이는 배열의 중간 값을 찾고 그보다 검색하는 수가 크면 오른쪽 배열에서 찾고 작으면 왼쪽배열에서 찾는 방식으로 해결하는 방식이다.
3. BS 함수의 인수로는 (시작, 끝, 검색할 수)가 들어가며 만약 BS(0, 5, 4)인 경우에는 인덱스 0, 1, 2, 3, 4 중에 4를 찾는다는 것을 의미한다.
4. 재귀적으로 해결한다.

💻 코드

//난이도 : 실버4
//시작 : 11:08
//끝 : 11:22
#include <iostream>
#include <algorithm>

using namespace std;

int A[100000]; //배열을 저장

//Binary Search 알고리즘
//BS(0, 4, 5)는 인덱스 0, 1, 2, 3에서 5를 찾는다는 의미
int BS(int start, int end, int search) { //시작, 끝, 검색할 숫자
	if (end - start == 1 && search == A[start]) { //배열의 크기가 1인 경우 남아 있는 숫자가 검색하는 수인지 확인하여 맞으면
		return 1; //1 반환
	}
	if (end - start == 1 && search != A[start]) { //검색하는 수가 아니면
		return 0; //0 반환
	}
	if (end - start == 0) { //배열의 크기가 0인 경우, 방어 코드
		return 0; //0 반환
	}

	int medium = (start + end) / 2; //중간 인덱스 값
	if (search == A[medium]) { //중간 인덱스의 값이 검색하는 수이면
		return 1; //1 반환
	}
	else { //중간 인덱스의 값이 검색하는 수가 아닌 경우
		if (search > A[medium]) { //검색하는 수가 중간 값보다 큰 경우
			return BS(medium, end, search); //오른쪽에서 다시 검색 재귀적, 이분할
		}
		else if (search < A[medium]) { //검색하는 수가 중간 값보다 작은 경우
			return BS(start, medium, search); //왼쪽에서 다시 검색 재귀적, 이분할
		}
	}
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	
	int N;
	cin >> N;
	for (int i = 0; i < N; i++) {
		cin >> A[i];
	}
	sort(A, A + N); //오름차순 정렬을 반드시 해주어야 이분탐색이 가능하다.
	int M;
	cin >> M;
	for (int i = 0; i < M; i++) {
		int tmp;
		cin >> tmp;
		cout << BS(0, N, tmp) << '\n';
	}

	return 0;
}