다익스트라 알고리즘

• 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알 수 있다.
• 음의 간선이 존재하는 경우 사용할 수 없다.
• 다익스트라 알고리즘은 일종의 다이나믹 알고리즘이라고 할 수 있으며 그 이유는 작은 최단 경로의 합이 전체적인 최단경로가 되기 때문이고 따라서 이전에 구한 최단 거리 정보를 그대로 사용한다.

다익스트라 알고리즘의 시간복잡도

• 가장 작은 간선의 값을 가진 노드를 찾을 때 선형 탐색을 이용한다면 $O(N^2)$
  • 그 이유는 가장 작은 노드를 찾을 때 for문이 쓰여 이 부분이 선형 탐색이라면 $O(N)$ 그 위에 시작 노드와 끝 노드를 뺀 나머지 노드를 모두 탐색해야하므로 for문에 쓰이기 때문에 이중 for문$O(N)$이 되기 때문이다.
• 힙을 이용한다면 루트 노트에 가장 작은 값이 항상 오기 때문에 선형 탐색을 할 필요가 없어서 시간 복잡도가 $O(NlogN)$이다.
  • priority_queue를 사용하여 구현한다.

다익스트라 알고리즘 예시

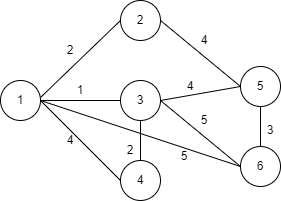
• d 배열은 출발 노드부터의 각 노드까지의 최단 거리 저장 배열
• v 배열은 방문 처리 배열로 F는 미방분 T는 방문
• 출발 노드가 1번노드인 경우 흐름
  

다익스트라 알고리즘 구현(선형탐색)

#include <iostream>

using namespace std;

int number = 6; //간선의 개수
int INF = 987654321; //무한 정의

int a[6][6] = {
	{0, 2, 1, 4, INF, 5},
	{2, 0, INF, INF, 4, INF},
	{1, INF, 0, 2, 4, 5},
	{4, INF, 2, 0, INF, INF},
	{INF, 4, 4, INF, 0, 3},
	{5, INF, 5, INF, 3, 0}
};

bool v[6] = { 0 }; //방문한 노드 표시, 방문하면  true, 미방문 false
int d[6] = { 0 }; //최단 거리 저장

int getSmallIndex() {
	int min = INF;
	int index = 0;
	for (int i = 0; i < number; i++) {
		if (d[i] < min && !v[i]) { //방문하지 않은 노드 중 가장 작은 노드의 인덱스 반환
			min = d[i];
			index = i;
		}
	}
	return index;
}

void dijkstra(int start) {
	for (int i = 0; i < number; i++) {
		d[i] = a[start][i];
	}
	v[start] = true; //방문처리
	for (int i = 0; i < number - 2; i++) { //시작 노드와 마지막 노드를 제외한 노드에 대해서만 반복하면 완성된다.
		int current = getSmallIndex(); //가장 거리가 작은 노드정보 가져옴
		v[current] = true; //방문처리
		for (int j = 0; j < number; j++) { //current로 부터 모든 j에 대해서 갱신
			if (!v[j]) { //방문하지 않은 노드인 경우 작은 값으로 최단거리 배열 업데이트
				d[j] = min(d[current] + a[current][j], d[j]); //current 노드를 거쳐 가는 것과 current 노드를 거쳐가지 않는 경우 중 작은 값으로 업데이트
				//연결되지 않은 경우 INF 이기 때문에 선택되지 않는다.
			}
		}
	}
}

int main() {
	dijkstra(0);
	for (int i = 0; i < number; i++) {
		cout << d[i] << " ";
	}


	return 0;
}

다익스트라 알고리즘 구현(우선순위 큐)

// 우선순위 큐를 이용한 다익스트라 구현
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int number = 6; //노드의 개수
int INF = 987654321; //무한 정의

vector<pair<int, int>> a[7]; //출발노드, 도착노드 간선 정보 벡터 //인덱스 1부터 사용
int d[7]; // 출발노드부터 각 노드 까지의 최단 거리 저장 배열로 인덱스 1부터 사용

void dijkstra(int start) {
	d[start] = 0; //자기 자신 거리는 0으로 초기화
	priority_queue<pair<int, int>> pq; //우선순위 큐 생성 <도착 노드, 거리> 
									   //우선 도착 노드 번호별로 내림차순 정렬 후 거리별 내림차순 정렬을 하는데
									   //여기서는 도착 노드의 번호 정렬은 의미 없고 거리별 내림차순만이 의미있게 사용한다.
									   //동일한 노드로 가는 거리가 여러개인 경우 거리 오름차순으로 정렬된다.
									   //또한 여기서는 오름차순 정렬이 필요하기 때문에 거리를 음수화 하여 저장한다.
	pq.push(make_pair(start, 0)); //자기 자신 <자기 자신, 거리 0>
	while (!pq.empty()) { //큐가 빌 때까지 실행
		int current = pq.top().first; //현재 위치 큐에서 꺼냄
		int distance = -pq.top().second; //현재 도착 노드까지 거리 꺼냄 
										 //이때 우선순위 큐는 내림차순 정렬이 기본이기 때문에 이를 오름차순 정렬처럼 사용하기 위해 거리를 음수화 하여 저장하였고 
										 //따라서 거리를 꺼낼 때 다시 음수화하여야 한다.
		pq.pop();
		if (d[current] < distance) continue; //현재 가지고 있는 최단 거리 배열의 값이 더 작다면 바로 다음으로 패스
											 //이는 최단 거리 검증이 완료된 것을 의미한다.
		for (int i = 0; i < a[current].size(); i++) { //current 노드에서 연결되어 있는 노드만을 확인
			int next = a[current][i].first;
			int nextDistance = distance + a[current][i].second; //인접 노드로 가는 거리
			if (nextDistance < d[next]) { //바로 가는 것보다 current 노드를 거쳐가는 것이 더 거리가 짧은 경우
				d[next] = nextDistance; //최단 거리 배열 업데이트
				pq.push(make_pair(next, -nextDistance)); //우선순위 큐에 새로 업데이트 된 최단 거리를 push한다. 
														 //이는 갱신된 최단 거리가 이 후에 다시 최단 거리인지 확인해야하기 때문이다.
			}
		}
	}
}

int main() {
	for (int i = 1; i <= number; i++) {
		d[i] = INF;
	}

	a[1].push_back(make_pair(2, 2));
	a[1].push_back(make_pair(3, 1));
	a[1].push_back(make_pair(4, 4));
	a[1].push_back(make_pair(6, 5));

	a[2].push_back(make_pair(1, 2));
	a[2].push_back(make_pair(5, 4));

	a[3].push_back(make_pair(1, 1));
	a[3].push_back(make_pair(4, 2));
	a[3].push_back(make_pair(5, 4));
	a[3].push_back(make_pair(6, 5));

	a[4].push_back(make_pair(1, 4));
	a[4].push_back(make_pair(3, 2));

	a[5].push_back(make_pair(2, 4));
	a[5].push_back(make_pair(3, 4));
	a[5].push_back(make_pair(6, 3));

	a[6].push_back(make_pair(1, 5));
	a[6].push_back(make_pair(3, 5));
	a[6].push_back(make_pair(5, 3));

	dijkstra(1);

	for (int i = 1; i <= number; i++) {
		cout << d[i] << " ";
	}



	return 0;
}