정렬
가장 큰 수 - Level 2
https://programmers.co.kr/learn/courses/30/lessons/42746
내 풀이 - 실패
def solution(numbers):
answer = ''
numbers.sort()
dic = {i:[] for i in range(0, 10)}
for i in range(len(numbers)):
s = int(str(numbers[i])[0])
if str(numbers[i])[-1] == "0":
dic[s].insert(0, numbers[i])
else:
dic[s].append(numbers[i])
for i in range(9, -1, -1):
while dic[i]:
answer += str(dic[i].pop())
return answer처음엔 재귀로 모든 조합들을 찾아서 max 값을 return 하려 했지만 타임리밋,,
그래서 큰 숫자들부터 앞자리에 배치하기로 했다.
우선 numbers 정렬 => sort()
dic 만들어서 0 ~ 9 의 숫자들 넣어줌
numbers 를 보면서 시작 값 s 에 해당하는 dic[s] 에 값 넣어주기
이 때, 0 으로 끝나는 숫자들은 insert 로 맨 앞에 넣어줌
ex) [3, 30, 34, 5, 9] => dic[3] = [30, 3, 34], dic[5] = [5], dic[9] = [9]
큰 숫자들부터 answer 에 붙여주고 return
그러나... 안됨!!
0 만 고려할게 아닌듯...
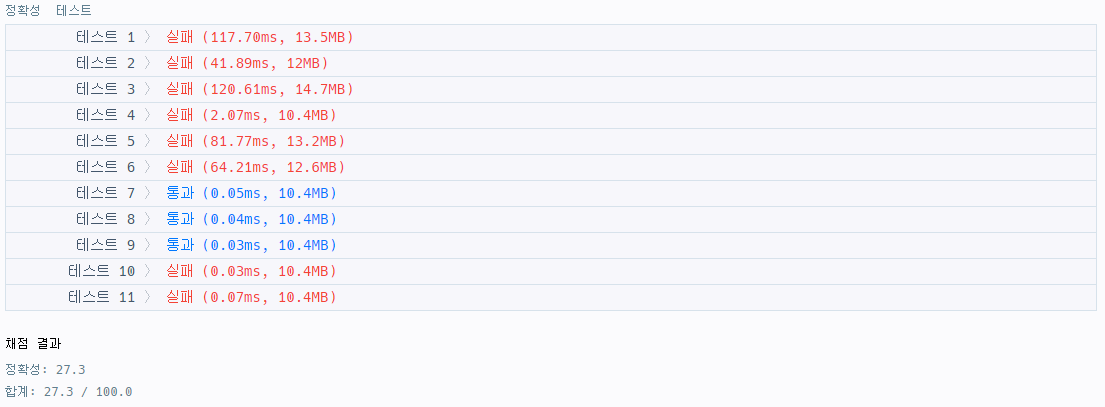
다른 사람의 풀이
def solution(numbers):
numbers = list(map(str, numbers))
numbers.sort(key=lambda x: x*3, reverse=True)
return str(int(''.join(numbers)))numbers 의 숫자들을 string 으로 변경
=> list(map(str, numbers)) 알아두자!!
정렬은 "numbers 값 * 3" 기준 & 역순으로!!
3 을 곱해주는 이유는 1,000 이하의 숫자들이기 때문에 세자리로 맞추기 위해서
ex) [3, 30, 34, 5, 9] => "9534330"
int 형일 때, 그냥 sort() => [34, 30, 9, 5, 3] (❌)
str 형일 때, 그냥 sort() => [9, 5, 34, 30, 3] (❌)
str 형일 때, 3 곱한 값으로 sort() => [999, 555, 343434, 333, 303030] => [9, 5, 34, 3, 30] (⭕)
000 처럼 모든 숫자가 0 인 경우도 있으므로 int 로 변환했다가 다시 string 으로 변환

H-Index - Level 2
https://programmers.co.kr/learn/courses/30/lessons/42747
내 풀이 - 통과
def solution(citations):
answer = 0
citations.sort()
idx = 0
for i in range(1, max(citations)):
while idx < len(citations) and citations[idx] < i:
idx += 1
if idx <= i and len(citations) - idx >= i:
answer = max(answer, i)
return answer우선 citations 정렬 => sort()
1 ~ max(citations) 의 범위에서 H-index 찾기
citations 에서의 i 위치를 idx 로 찾아서
"h 번 이상 인용된 논문이 h 편 이상 & 나머지 논문이 h 번 이하" 인지 확인
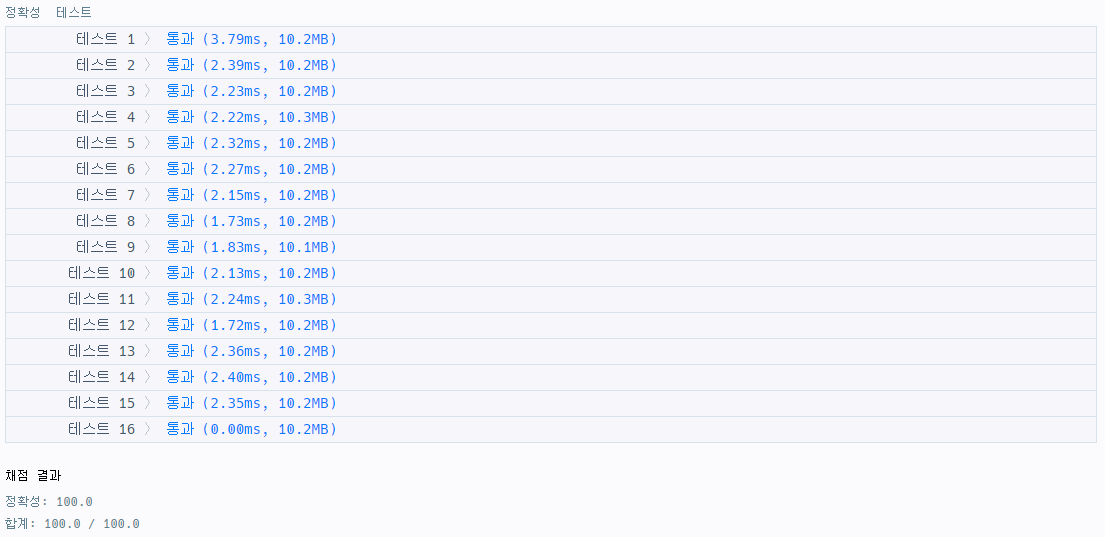
다른 사람의 풀이
def solution(citations):
citations.sort()
l = len(citations)
for i in range(l):
if citations[i] >= l-i:
return l-i
return 0더 간단한 천재같은 풀이
정렬 후, "0 ~ citations 의 길이" 의 범위만 확인
if citations[i] >= l-i:
=> citations[i] : h
=> l-i : h 번 이상 인용된 논문의 개수
ex) [0, 1, 3, 5, 6]
=> 0 >= 5, 1 >= 4, 3 >= 3 => return 3
ex) [0, 1, 5, 6]
=> 0 >= 5, 1 >= 4, 5 >= 2 => return 2
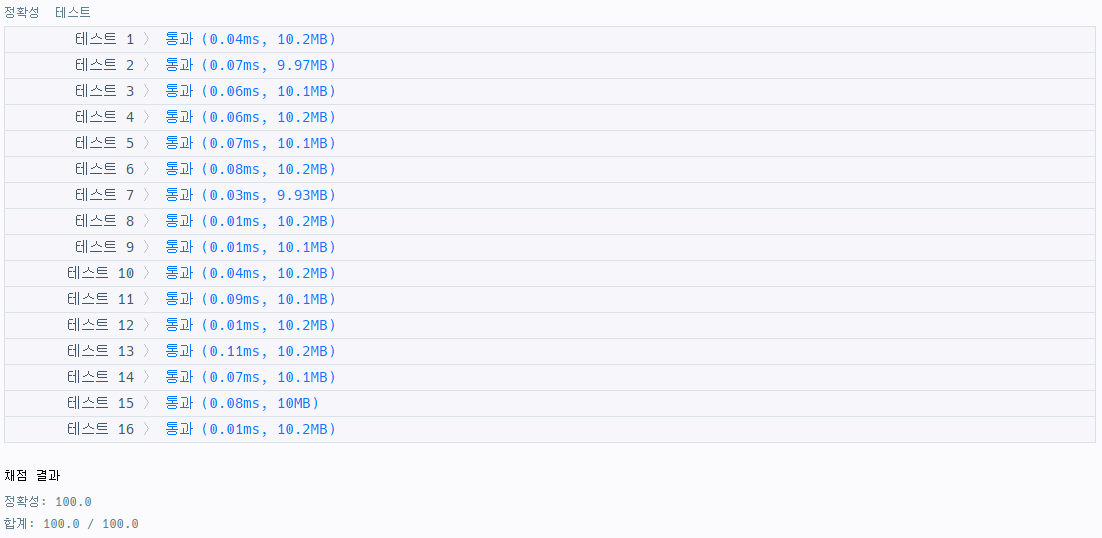
훨씬 빠르다
완전탐색
소수 찾기 - Level 2
https://programmers.co.kr/learn/courses/30/lessons/42839
내 풀이 - 통과
combinations = set()
def solution(numbers):
global combinations
def comb(nums, c):
if c and int(c) > 1:
combinations.add(int(c))
if len(nums) == 0:
return
for i in range(len(nums)):
comb(nums[:i] + nums[i+1:], c+nums[i])
comb(numbers, "")
answer = 0
for c in combinations:
isPrime = 1
for i in range(2, int(c**0.5)+1):
if c % i == 0:
isPrime = 0
break
if isPrime:
answer += 1
return answer종이 조각으로 만들 수 있는 모든 숫자의 경우를 combinations 에 저장
=> 재귀 함수 comb 를 이용
구한 숫자들은 소수인지 판단하기 위해 2 ~ 루트 c 까지 약수가 있는지 확인
소수들의 개수만 세줘서 return
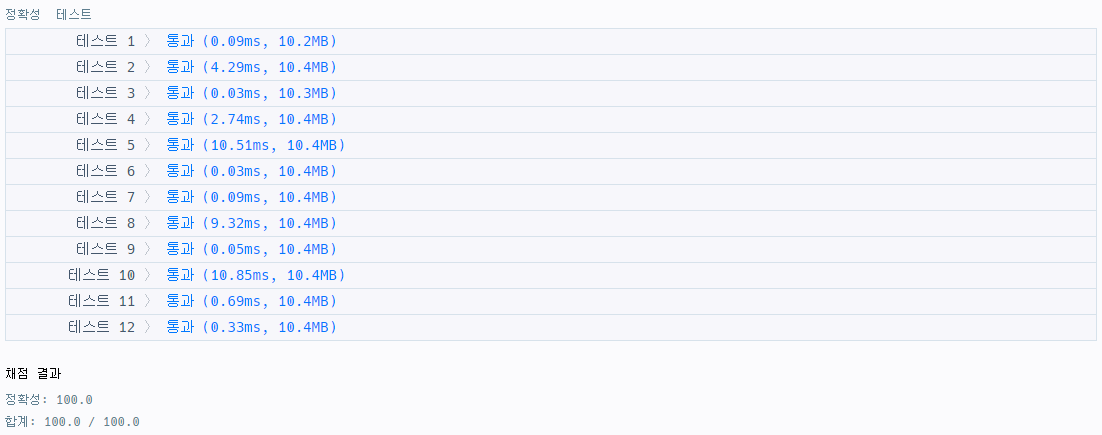
다른 사람의 풀이
from itertools import permutations
def solution(n):
a = set()
for i in range(len(n)):
a |= set(map(int, map("".join, permutations(list(n), i + 1))))
a -= set(range(0, 2))
for i in range(2, int(max(a) ** 0.5) + 1):
a -= set(range(i * 2, max(a) + 1, i))
return len(a)정말 천재같은 코드...
1) 숫자들의 조합 구하기
a |= set(map(int, map("".join, permutations(list(n), i + 1))))
permutations(list(n), i + 1))=> 리스트n을 이용한i+1길이의 조합- 문자열로 합친 후 int 로 바꿔서
a에 저장 |==> 중복 제거
2) a 에서 0 ~ 1 값은 제거
(=> set 를 - 연산을 이용해서 제거 가능하다는 걸 첨 알았다,,)
3) 소수 찾기
범위: 2 ~ 루트 (최댓값)
a -= set(range(i * 2, max(a) + 1, i))
- range 를 이용해서
i의 배수들은a에서 모두 제거
에라토스테네스 체
:2 ~ 루트 n까지의 숫자들을 보면서 각 숫자들의 배수들을 미리 없애주는 방식def prime_list(n): # 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주) sieve = [True] * n # n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사 m = int(n ** 0.5) for i in range(2, m + 1): if sieve[i] == True: # i가 소수인 경우 for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정 sieve[j] = False # 소수 목록 산출 return [i for i in range(2, n) if sieve[i] == True]시간 복잡도:
O(N**0.5)
카펫 - Level 2
https://programmers.co.kr/learn/courses/30/lessons/42842
내 풀이 - 통과
def solution(brown, yellow):
answer = []
for i in range(yellow, 0, -1):
w = i
h = yellow // i + yellow % i
b = w * 2 + h * 2 + 4 + (w*h - yellow)
if b == brown:
if w > h:
return [w+2, h+2]
else:
return [h+2, w+2]
return answeryellow 의 형태가 어떨지 모르기 때문에 (항상 정사각형의 모양이란 보장이 X)
yellow ~ 1 까지의 모든 범위 확인
가로 w = i
세로 h = yellow // i + yellow % i
yellow // i: ㅁ 모양처럼 모든 줄이i개만큼 꽉 참
yellow % i: ㄱ 모양처럼 일부가 비어있는 경우를 합한 것이 세로가 됨
yellow 를 감싼 브라운의 개수 b = w * 2 + h * 2 + 4 + (w*h - yellow)
w * 2 + h * 2: 순수 yellow 를 감싼 브라운
4: 4 개의 모서리
(w*h - yellow): ㄱ 모양처럼 비어있는 곳을 채워주는 브라운
if b == brown: => 더 큰 값을 가로로 잡아서 return
다른 사람의 풀이
def solution(brown, yellow):
for i in range(1, int(yellow**(1/2))+1):
if yellow % i == 0:
if 2*(i + yellow//i) == brown-4:
return [yellow//i+2, i+2]이 문제는 역시 공식이 있었다..^^
1 ~ 루트 yellow 까지의 숫자들 중에 yellow 의 약수
그 중에서도 if 2*(i + yellow//i) == brown-4: 를 만족하는 i 찾기
확실히 더 빠르다^^
