❗️해당 게시글은 공부한 내용을 정리한 글입니다.
❗️잘못된 내용이 있을 수 있습니다.
❗️혹시 잘못된 내용이 있다면 댓글로 피드백 부탁드리겠습니다! 🙇‍♂️

알고리즘이란?

• 알고리즘은 9세기 경 아라비아의 천문학자이자 수학자인 알고리즈미(al-Khowarizmi)의 이름에서 유래되었다.
• 알고리즈미는 십진법에 의해 덧셈, 뺄셈, 곱셈, 나눗셈, 제곱근, 원주율을 구하는 방법을 아랍어로 기록해 놓았는데, 이런 식으로 사칙연산 및 다양한 산술의 해를 구하는 절차를 공식화 해놓은 기록이 후에 알고리즘으로 발전되었다.
• 즉, 알고리즘은 어떤 문제를 해결하기 위해서 일련의 절차를 정의하고, 공식화한 형태로 표현한 일종의 문제의 풀이 방법, 해(解)를 의미한다. 이런 알고리즘은 프로그래밍에서는 input 값을 통해 output 값을 얻기 위한 계산 과정을 의미한다.

알고리즘 조건

• 입력(Input): 알고리즘은 출력에 필요한 자료를 입력 받을 수 있어야 한다.
• 출력(Output): 알고리즘은 실행이 되면 적어도 한 가지 이상의 결과를 반드시 출력해야 한다.
• 유한성(Finiteness): 알고리즘은 유한한 명령어를 수행한 후, 유한한 시간 내에 종료해야 한다.
• 명확성(Definiteness): 알고리즘의 각 단계는 단순하고 명확해야 하며, 모호해서는 안된다.
• 효율성(Efficiency): 알고리즘은 가능한 한 효율적이어야 한다.

알고리즘의 중요성

알고리즘은 프로그래밍 뿐만 아니라 일상생활에서도 다양한 문제를 해결하는 데에 활용할 수 있다. 좋은 알고리즘은 절차가 명확하게 표현되어 있고, 효율적이므로 다양한 문제 해결 과정에서 나타나는 불필요한 작업들을 줄여줄 수 있다.

시간 복잡도

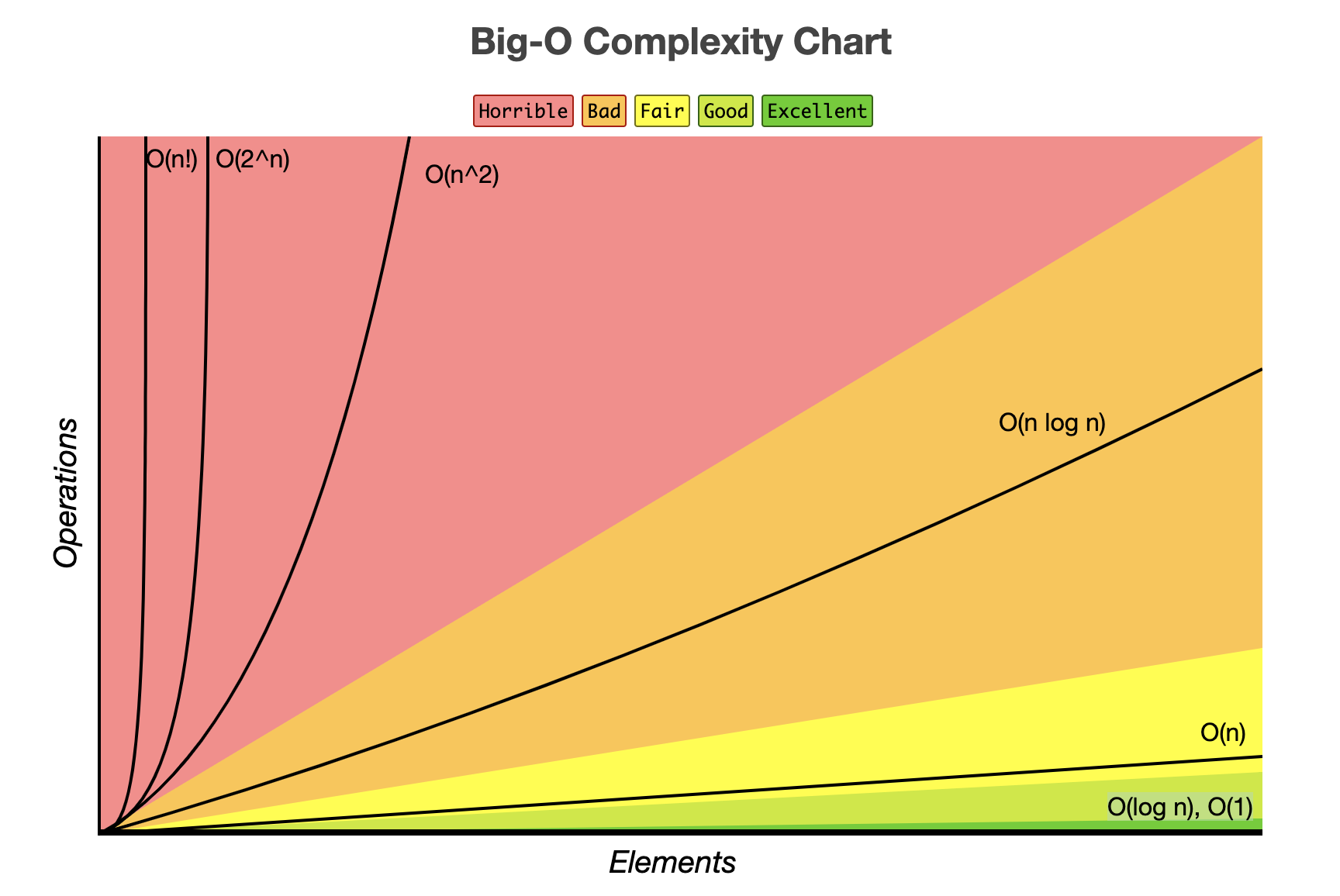
시간 복잡도란 컴퓨터 프로그램의 입력값과 연산 수행 시간의 상관관계를 나타내는 척도이다.

입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가? 를 의미한다.

Big-O 표기법

시간 복잡도를 표기하는 방법은 다음과 같다.

• Big-O(빅-오)
• Big-Ω(빅-오메가)
• Big-θ(빅-세타)

위 세 가지 표기법은 시간 복잡도를 각각 최악, 최선, 중간(평균)의 경우에 대하여 나타내는 방법이다. 이 중에서 Big-O 표기법이 가장 자주 사용된다.

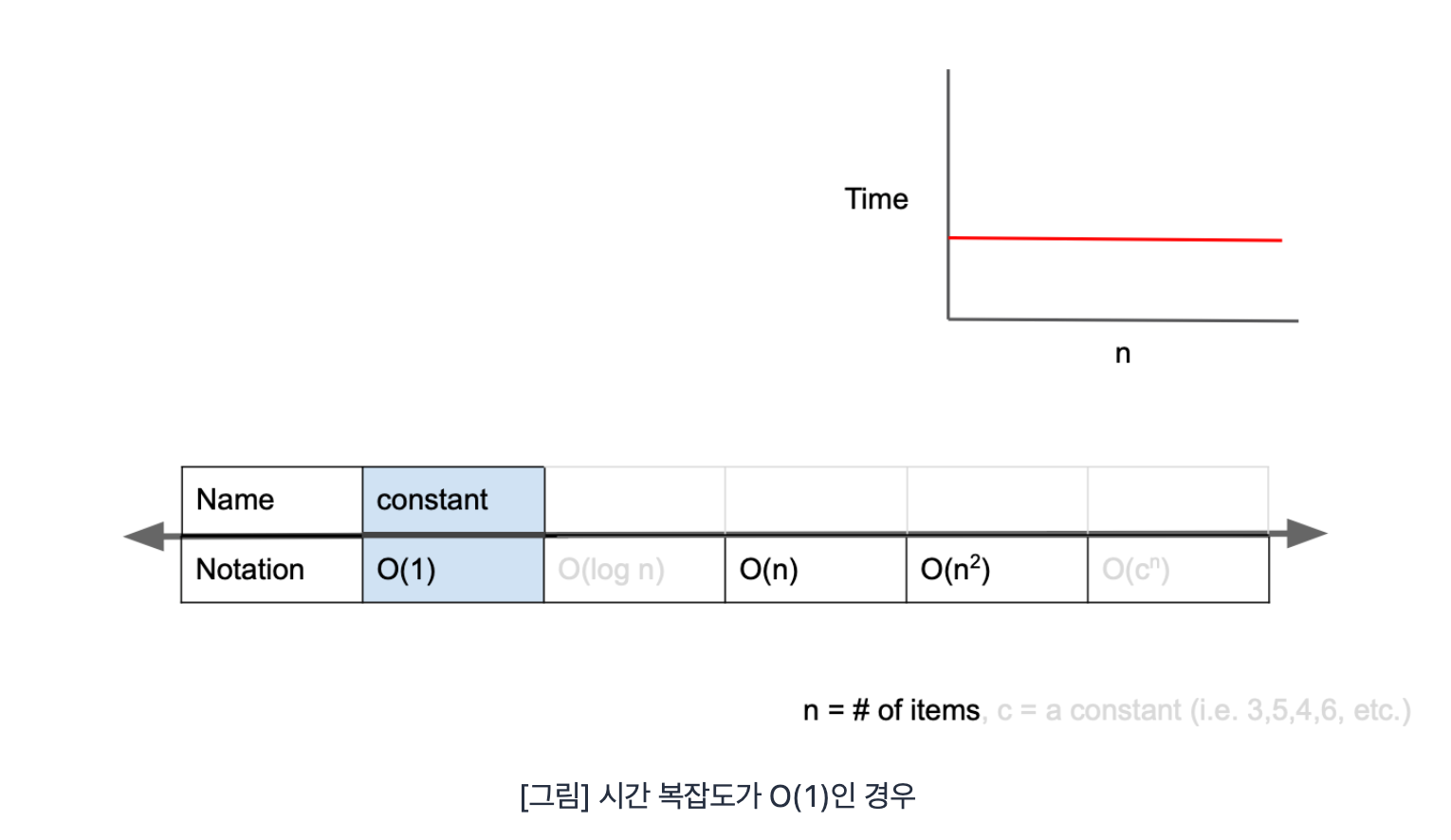
O(1)

O(1)는 constant complexity라고 하며 입력값이 증가하더라도 시간이 늘어나지 않는다. 다시 말해 입력값의 크기와 관계없이 즉시 출력값을 얻어낼 수 있다는 의미이다.

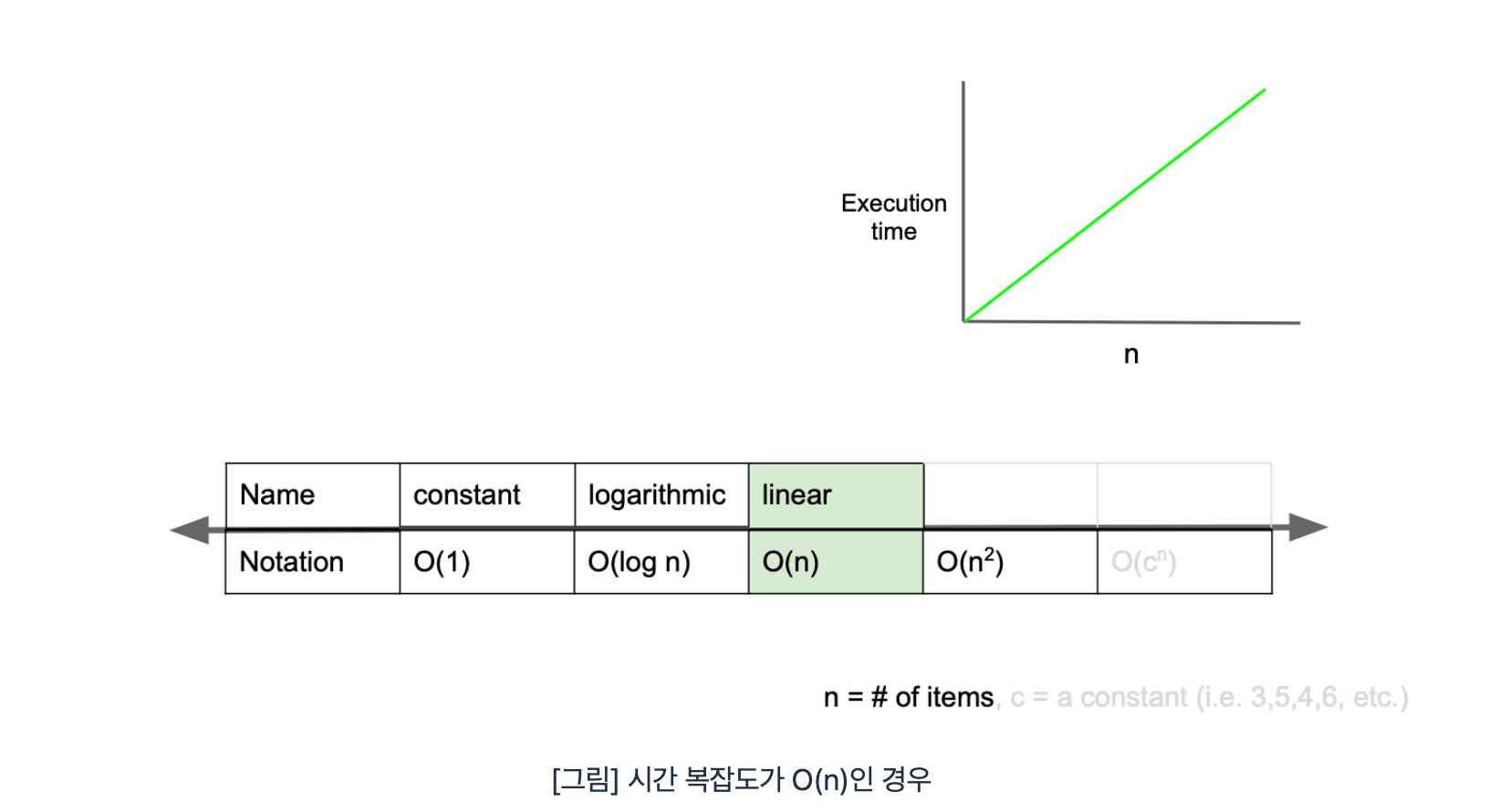
O(n)

O(n)은 linear complexity라고 부르며 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다.

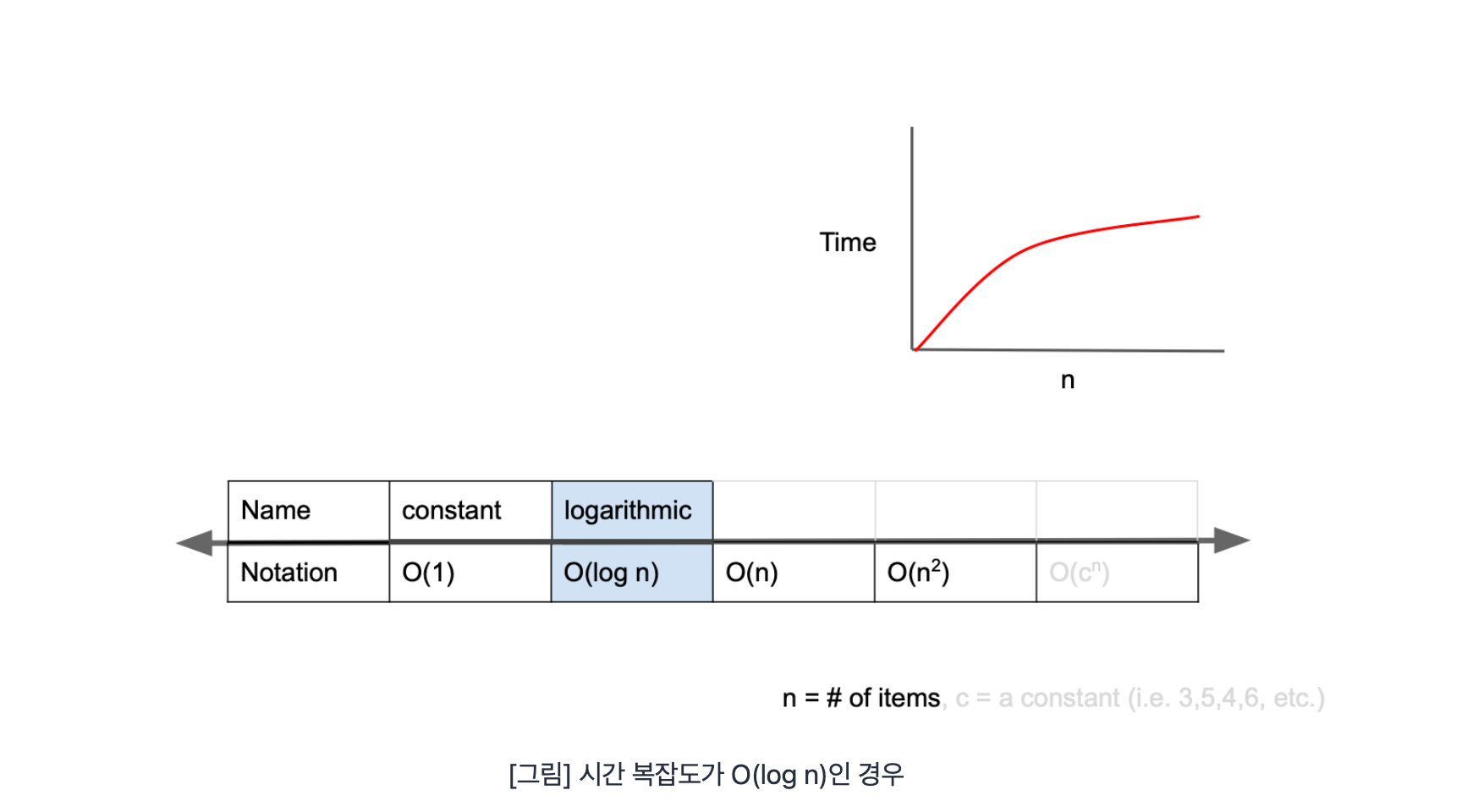
O(log n)

O(log n)은 logarithmic complexity라고 부르며 Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다. 이진 탐색의 경우를 예로 들 수 있다.

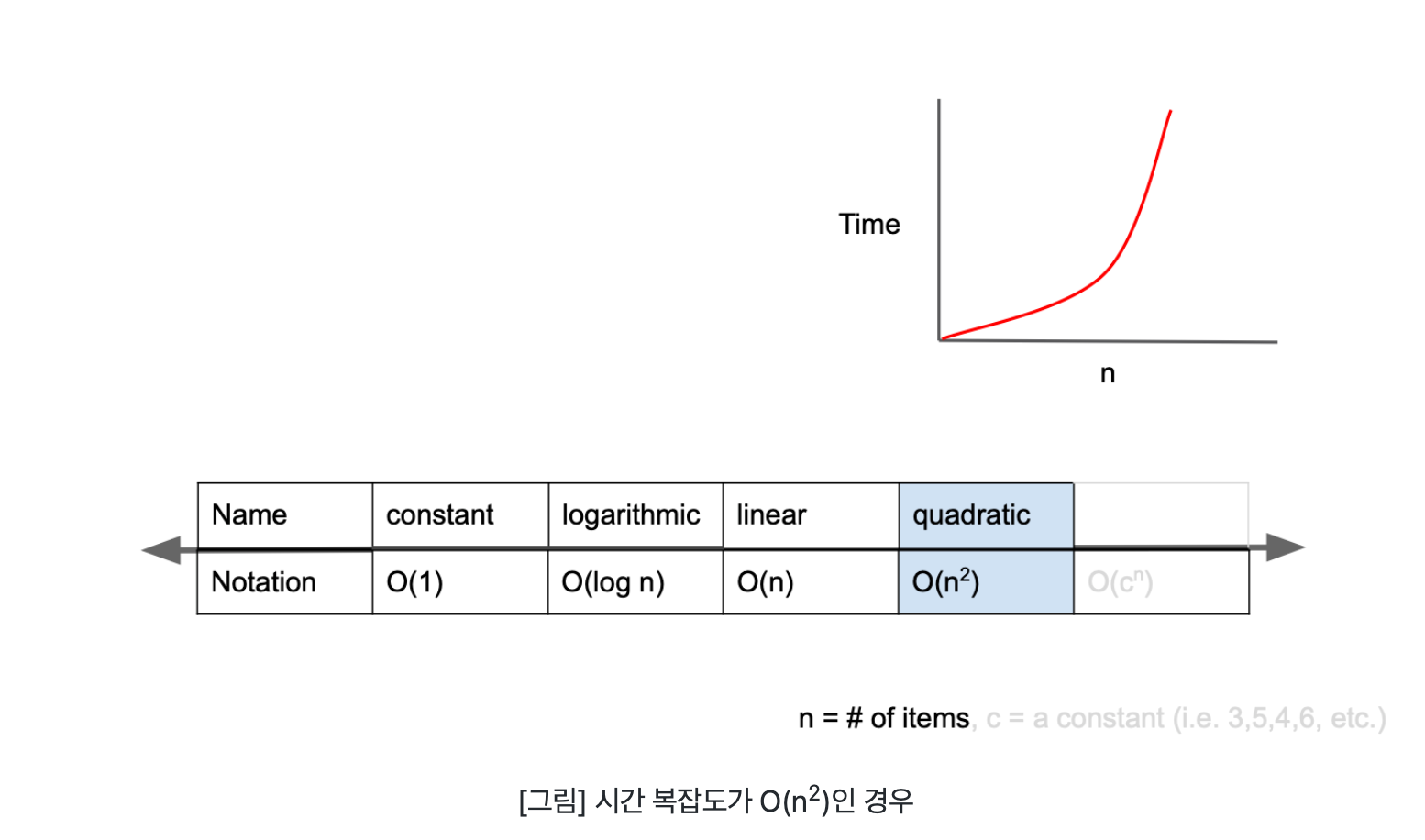
O(n²)

O(n^2)은 quadratic complexity라고 부르며 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다. 예를 들어 입력값이 1일 경우 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 된다면 이 알고리즘의 시간 복잡도는 O(n2)라고 표현한다.

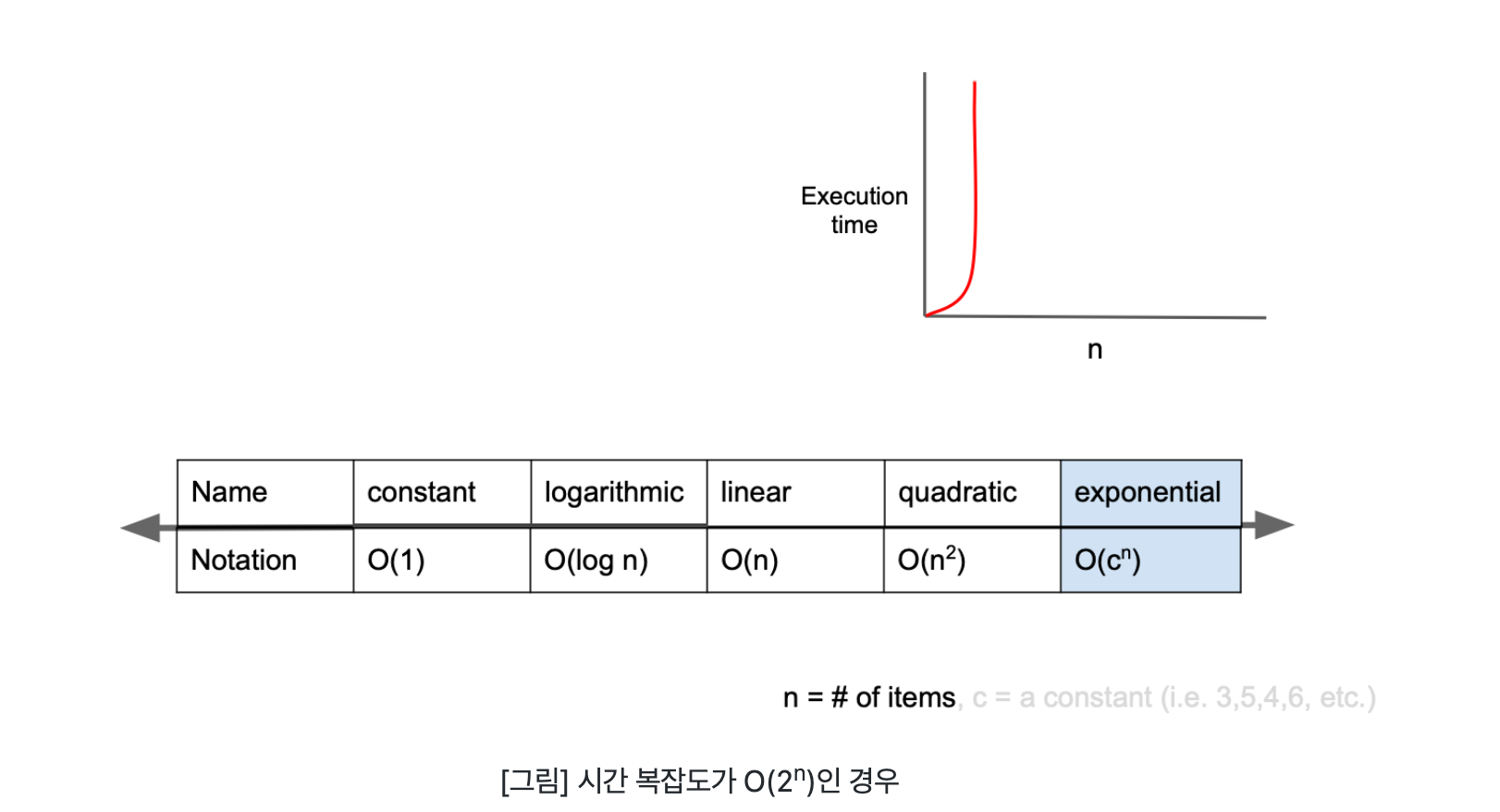
O(2^n)

O(2^n)은 exponential complexity라고 부르며 Big-O 표기법 중 가장 느린 시간 복잡도를 가집니다. 피보나치 수열이 시간 복잡도 O(2^n)의 대표적인 예이다.

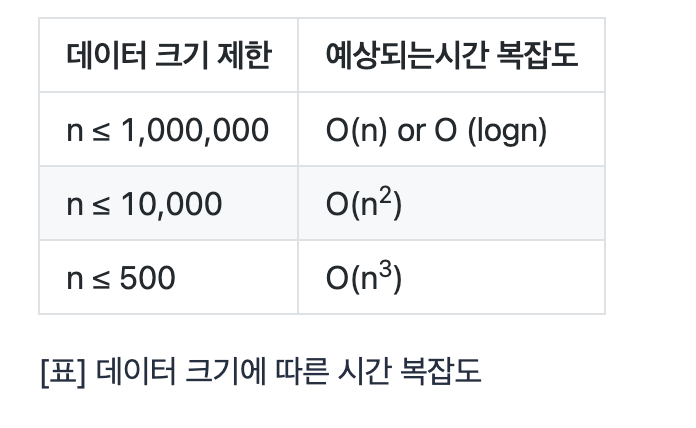
데이터 크기에 따른 시간 복잡도

코딩 테스트 문제를 풀 때 시간제한과 주어진 데이터 크기 제한을 보고 시간 복잡도를 어림잡아 예측해볼 수 있다.

공간 복잡도(Space Complexity)

공간 복잡도는 알고리즘이 수행되는 데에 필요한 메모리의 총량을 의미한다. 즉 프로그램이 필요로 하는 메모리 공간을 산출하는 것을 의미한다.

프로그램이 요구하는 공간은 고정적인 공간과 함께 가변적인 공간을 함께 요구한다. 여기서 집중해야 할 부분은 가변적인 공간이다. 왜냐하면 고정적인 공간은 처리할 데이터의 양에 무관하게 항상 요구되는 공간으로서 프로그램의 성능에 큰 영향을 주지 않기 때문이다. 그러나 가변적인 공간은 처리할 데이터의 양에 따라 다르게 요구되는 공간으로서 프로그램의 성능에 큰 영향을 준다.

공간 복잡도 계산도 빅 오(Big-O) 표기법으로 표현한다.

공간 복잡도 예시

function factorial(n) {
	if(n === 1) {
		return n;
	}
	return n * factorial(n - 1);
}

함수 factorial은 재귀함수로 구현되어 있다. 변수 n에 따라 변수 n이 n개가 만들어지게 되며 factorial 함수를 재귀함수로 1까지 호출할 경우 n부터 1까지 스택에 쌓이게 된다. 따라서 해당 함수의 공간 복잡도는 O(n)이라 볼 수 있다.

공간 복잡도의 중요성

보통 때의 공간 복잡도는 시간 복잡도보다 중요성이 떨어진다. 왜냐하면 시간이 적으면서 메모리까지 지수적으로 증가하는 경우는 거의 없으며 시간 내에 발생하는 메모리 문제들은 보통 알고리즘을 구현할 때에 발생하는 문제이기 때문이다.

때에 따라 공간 복잡도를 중요하게 보는 경우가 있다. 동적 계획법(Dynamic Programming)과 같은 알고리즘이나 하드웨어 환경이 매우 한정되어 있는 경우이다. 동적 계획법은 알고리즘 자체가 구현 시 메모리를 많이 요구하기 때문에 입력 값의 범위가 넓어지면 사용하지 못하는 경우도 많고, 하드웨어 환경이 매우 한정되어 있는 경우(ex. 임베디드, 펌웨어 등)라면 가용 메모리가 제한되어 있기 때문이다.