
왔다리~ 갔다리~ 누구냐 넌!
 출처 : 무한도전
출처 : 무한도전
Alternating Series🎆
 출처 : 네이버 영어사전
출처 : 네이버 영어사전
사전의 정의대로, 부호가 번갈아 나오는 요런 친구다.
지난 글에서도 그랬듯이, 이 급수의 수렴여부를 판단해야하는데... 이번엔 무슨 Test인고?
Alternating Series Test📜
부호를 제외한 수열의 항을 이라고 할 때,
이 Eventually decreasing하고, 이면, 해당 Alternating Series는 Convergent하다.
Proof📚
그 증명은 다음과 같다.
Monotonic 하고 Bounded 되면 Convergent 하다는 사실을 기억하는가?
-
위의 Alternating Series를 첫번째 항부터 2개씩 묶으면
이렇게 되는데, decreasing하는 수열이라고 했으니 각 묶음은 양수이다.
양수인 묶음들이 계속 더해진다는 것은? 급수가 Increasing(Monotonic)이라는 뜻이다. -
이번에는 두번째 항부터 2개씩 묶으면
마찬가지로 각 묶음이 양수이니,
급수가 보다 작은, Bounded라는 뜻이다.
그러면 Monotonic Sequence Theorem에 의해서 은 수렴하고,
Alternating Series Test의 첫번째 condition까지 고려하면,
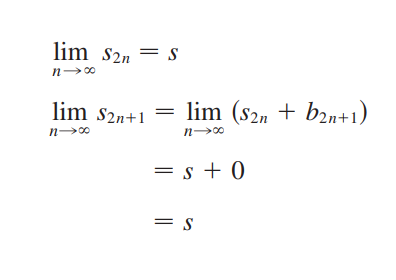
위 과정으로 홀수와 짝수 두 경우 모두 수렴함을 볼 수 있다!
Estimating Sums of Alternating Series
Alternating Series Estimation Theorem
Alternating Series에서 아래 두 condition이 만족하면, 즉 수렴하면 성립하는 식이 아래 식이다.
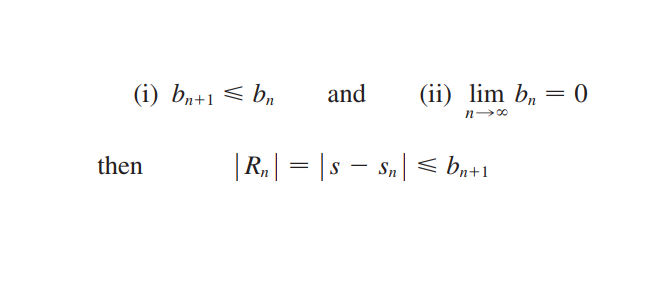
Proof📚
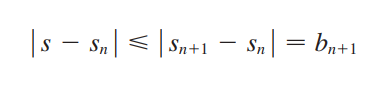
끝!
 출처 : MBC
출처 : MBC
😨아 알았어요...
위에서 설명했지만, 간단한 그림으로 설명하자면, (웃김주의)
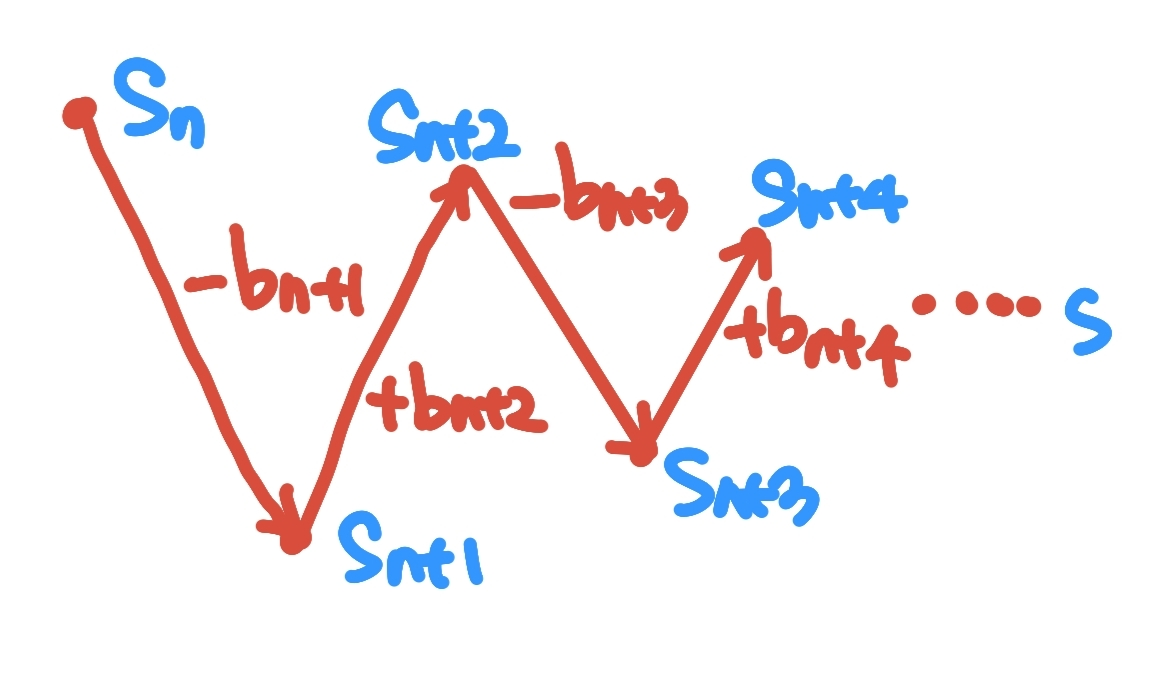
진짜 웃었다면 나 울어... 이 decreasing하는 수열이기에, 이렇게 된다!
그림을 보고, 위에 식을 다시 보고 오면 이해가 될 것이다!
Absolutely Convergent
만약 이 convergent하면,
급수 은 absolutely convergent하다.
그리고 그말은, 급수 이 convergent하다는 뜻이다.
정의 자체는 매우 간단하다! 증명도 간단하다!
Proof📚
이 어떤 부호로 이루어져 있던 간에, 아래 식은 무조건 성립한다.
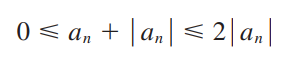
근데 가정이 "이 convergent하면" 이기에,
당연히 그 상수배인 도 convergent, 위 부등식의 가운데에 있는 도 convergent.
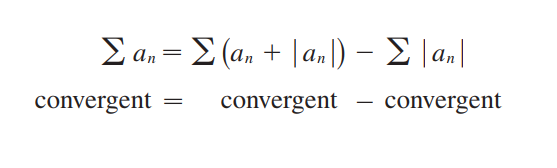
우잉? 너무나도 당연하다. 아님말고
Conditionally Convergent
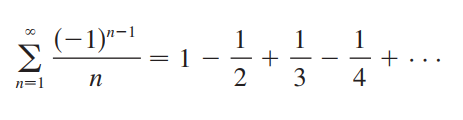
위의 수식에 절댓값을 붙인 은 우리에게 매우 익숙한데, 바로, p = 1 인 p-series(Harmonic Series)!
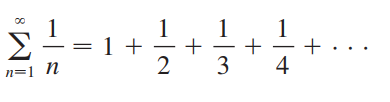
근데 우리는 가 divergent하다는 것,
즉, 원래 급수 가 Absolutely convergent하지 않다는 것을 안다.
그런데, 원래 친구는 decreasing하고 0으로 수렴하는 을 갖는,
Convergent한 Alternating Series이다.
이처럼 Convergent하지만, Absolutely convergent하지 않은 급수 을
Conditionally Convergent하다고 한다!
Ratio and Root Tests📜
Absolutely convergent하면 convergent하다고 했으니까...
그러면 일단 Absolutely Convergent한지 먼저 확인해보는게 좋겠네요??
맞다! Absolutely Convergent의 여부를 확인하기 위한 Tool들이 바로....
Ratio Test
Ratio? 등비급수의 r이 Ratio라는 것을 안다면 거의 다 안거나 다름없다.

영어만 보면 속이 울렁거릴 당신을 위해 한줄 요약하자면,
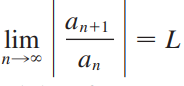
이 친구가 1보다 큰지 / 작은지 / 같은지에 따라서 Convergence가 결정된다는 말이다.
1이랑 비교해...? 등비급수...?
Proof📚
맞다! 등비급수, Geometric Series랑 비교하면 된다.
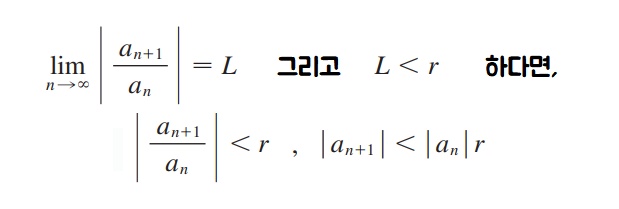
위의 식을 확장하고, 전에 배웠던 Direct Comparison Test를 이용하면,
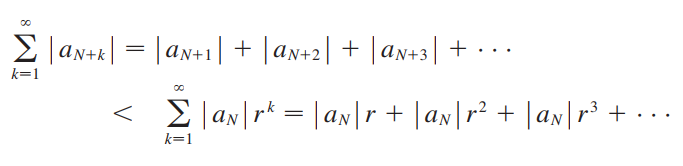
그렇기 때문에, L, Ratio가
1보다 작으면 Convergent / 1보다 크면 Divergent라는 것이다.
Root Test
비슷하다! 아까와 달리 n제곱된 항의 급수에 매우 용이하다.

주의해야할 사항은, 둘다 일 때는, 수렴여부가 결정되지 않는다는 것이다!
이 점은 다음 내용, Power Series에서 다뤄질 예정이다 :)
읽어주셔서 감사하구용,,,고맙구용,,,하트도 눌러주면 더 고맙구용,,, 댓글도,,,
 출처 : 유튜브 총몇명
출처 : 유튜브 총몇명
넵... 갈게욧!
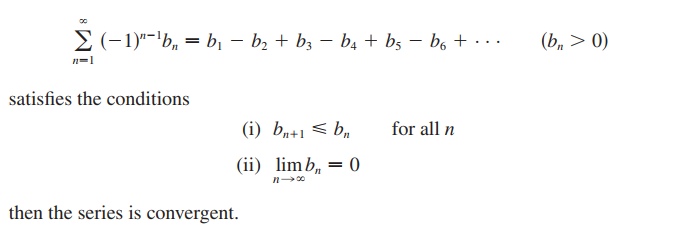

시험공부하는데 잘 보고가여