시작하며,

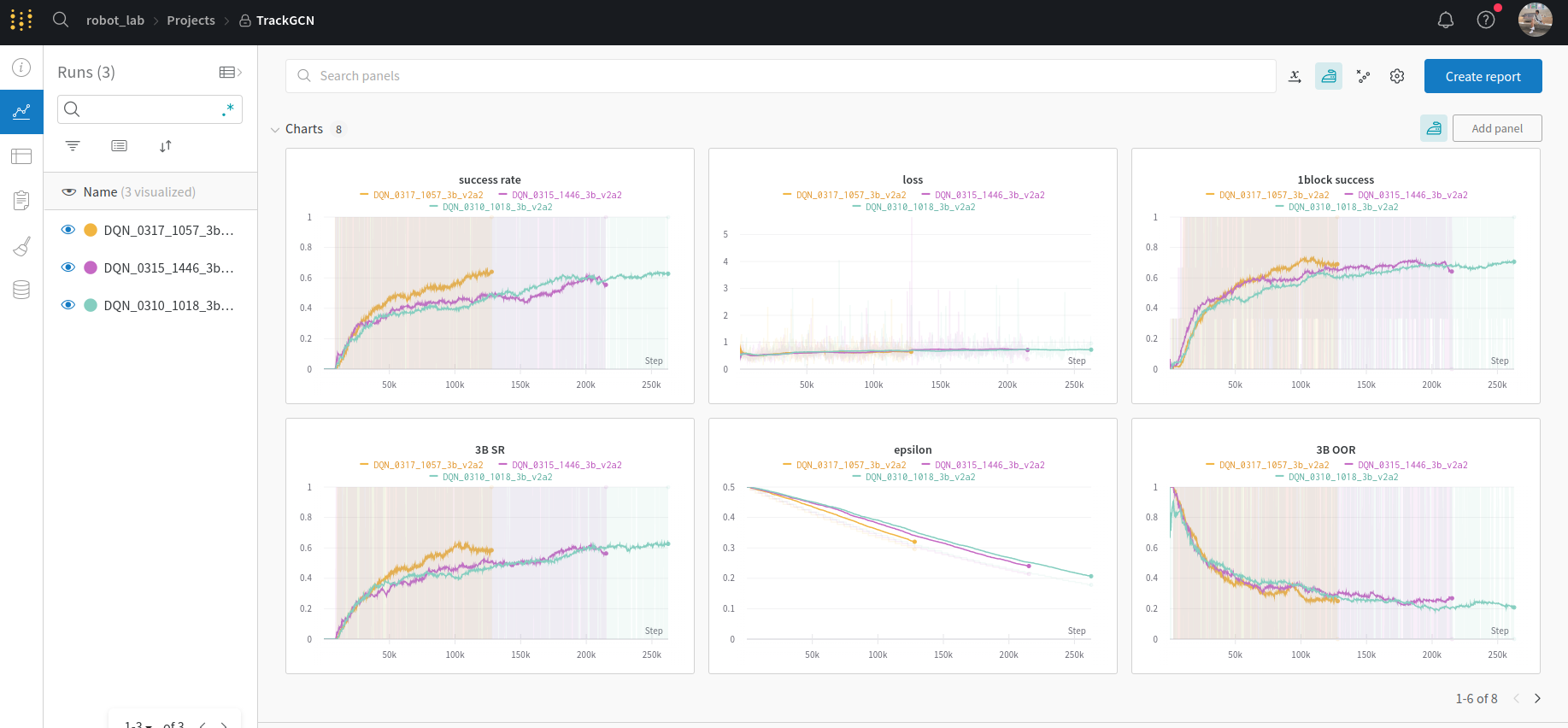
일단 졸업 연구는 꾸준히 진행하고 있습니다! SDFGCN의 front-end인 object matching 부분을 3개로 바꿔서 위와 같이 wandb로 plotting 하고 있습니다. 그 뒤엔 완전히 새로운 architecture인 coherent point drift로 rigid body의 transformation을 찾아 pick-and-place 방식으로 물체를 재배열하려고 합니다. 그렇게 이번엔 Point Set Registration: Coherent Point Drift와 Unsupervised 3D Link Segmentation of Articulated Objects With a Mixture of Coherent Point Drift를 참조하여 앞으로 활용할 개념을 재정비해보려고 합니다. 졸업 연구 기간이 8주밖에 남지 않은 만큼 더욱더 빠르게 hustle 해야겠어요.

EM과 optimal rotation matrix의 closed-form solution을 배경지식으로 활용합니다.

EM: https://velog.io/@jpseo99/Expectation-Maximization
optimal rotation matrix: https://velog.io/@jpseo99/closed-form-solution-of-the-rotation-matrix

Point Set Registration: Coherent Point Drift (For Rigid Body)

1. rigid / non-rigid transformation

rigid transformation: translation, rotation, scaling
non-rigid transformation: anisotropic scaling, skews

논문에서는 rigid transformation뿐만 아닌 non-rigid transformation까지 범용적으로 다룹니다. 하지만, 저의 연구 object matching은 rigid body만을 input으로 다루기 때문에 non-rigid related part는 생략했습니다. rigid transformation은 위에서 명시한 대로 평행이동, 회전, 스케일링만 가능합니다. non-rigid transformation은 이방성 스케일링, 왜곡까지 포함합니다. 한편, Non-rigid transformation은 real-world에서 굉장히 자주 발생합니다. deformable motion tracking, shape recognition 그리고 medical image registration 등이 그 예시입니다. 여유가 생겼을 때, 차근차근 살펴보면 재밌겠다는 생각이 드네요!

2. Problem Formulation (general case)

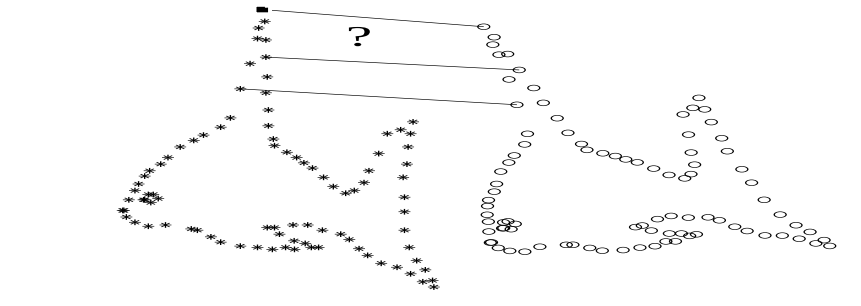
두개 point sets의 alignment를 probability density estimation 문제의 관점으로 바라봅니다. 둘 중 하나의 point set은 Gaussian mixture model centroids로 보고 나머지 하나는 data points로 봅니다. optimum에서 두 point sets가 aligned 되고 correspondence는 주어진 data point에 대한 GMM posterior probability로 구할 수 있습니다. 이 방법론의 핵심은 GMM centroids를 강제하여 일관적으로 (coherently) 움직여 point sets의 topological structure을 유지하는 것에 있습니다.

$D$: point sets의 차원
$N$: data points (첫번째 point sets) 의 개수
$M$: GMM centroids (두번째 point sets) 의 개수
$X$: data points (첫번째 point sets), $N×D$ matrix
$Y$: GMM centroids (두번째 point sets), $M×D$ matrix
$T (Y, θ)$ - Y에 Transformation (θ를 매개변수로 가지는) T를 적용 했을 때의 결과입니다. T는 rigid, non-rigid transformation을 전부 포함합니다.
$I$: identity matrix
$1$: 1로 가득 찬 column vector (차원은 때에 따라 다릅니다)
$d(a)$ - vector a의 값을 원소로 가지는 diagonal matrix

3. Expectation of the complete negative log-likelihood function (general case rigid body)

우리는 $Y$를 GMM centroids로 생각하고 $X$를 이 GMM mixture에 의해 생성된 points라고 생각합니다. 이때, GMM 확률밀도함수를 아래와 같이 표현할 수 있습니다.

$p(x) = \sum_{m = 1}^{M + 1}{p(m)p(x|m)}$

여기서 $m = 1, 2, 3, ..., M$일 때 $p(x|m)$은 아래와 같습니다.

$p(x|m) = \ {1 \over (2 \pi \sigma^2)^{D/2}} exp(-{1 \over 2}({|x-y_m| \over \sigma})^2)$

mixture model의 noise와 outliers를 위해 $m = M + 1$일 때는

$p(x|M + 1) = {1 \over N}$

으로 설정했습니다.

우리는 동일한 분산 $\sigma^2$과 membership probability $p(m) = {1 \over M}, m=1,2,...,M$을 활용했습니다.
0과 1사이의 weight $w$에 대해 mixture model의 확률 밀도 함수는 아래와 같습니다.

$p(x) = w {1 \over N} + (1-w) \sum_{m = 1}^{M}{1 \over M}p(x|m)$

EM 알고리즘을 위한 complete negative log-likelihood의 기댓값(objective function)은 아래와 같습니다.

$\sum_{n = 1}^{N}\sum_{m = 1}^{M+1}P^{old}(m|x_n) \space log(p^{new}(m)p^{new}(x_n|m))$

위의 objective function을 $\theta, \sigma^2$와 관계없는 항을 제거한 뒤에 나타내면 아래와 같습니다. $\theta, \sigma$에 대한 미분을 통해 M-step을 진행하기 때문에 그 이외의 항은 상수로 해석할 수 있기 때문입니다.

${1 \over {2 \sigma^2}}\sum_{n = 1}^{N}\sum_{m = 1}^{M+1}P^{old}(m|x_n) \space |x_n-T(y_m,\theta)|^2+{N_PD \over 2}log \sigma^2, N_p = \sum_{n = 1}^{N}\sum_{m = 1}^{M}P(m|x_n)$

여기서 GMM component의 posterior probabilities는 아래와 같습니다.

$P^{old}(m|x_n) = {exp(-{1 \over 2}({|x-T(y_m, \theta^{old})| \over \sigma^{old}})^2) \over {\sum_{m = 1}^{M} exp(-{1 \over 2}({|x-T(y_k, \theta^{old})| \over \sigma^{old}})^2) + c}}$
$c = (2 \pi \sigma^2)^{D/2} {w \over 1-w}{M \over N}$

4. E-step and M-step (rigid body)

rigid point set registration problem에서 GMM centroid 위치의 transformation을 아래와 같이 정의합니다.

$T(y_m; R, t, s) =sRy_m + t$
$R_{D×D}$는 회전 변환이고 $t_{D×1}$는 평행이동, $s$는 scale을 나타냅니다.

아래의 optimal problem을 해결하는 것이 M-step 입니다.

$Q(R,t,s, \sigma ^ 2) = {1 \over {2 \sigma^2}}\sum_{n = 1}^{N}\sum_{m = 1}^{M+1}P^{old}(m|x_n) \space |x_n-sRy_m-t|^2+{N_PD \over 2}log \sigma^2, N_p = \sum_{n = 1}^{N}\sum_{m = 1}^{M}P(m|x_n)$
$min Q(R,t,s, \sigma ^ 2), s.t. R^TR=I, \space det(R)=1$

위 문제는 generalized weighted absolute orientation problem 입니다. 아래의 lemma를 활용해서 이 문제에 접근해볼 수 있습니다.

Q를 t에 대해서 편미분해서 0이 되는 값을 찾으면 아래와 같습니다.

$t={1 \over N}X^TP^T1-sR{1 \over N}Y^TP1=µ_x-sRµ_y$
$P_{mn}=p^{old}(m|x_n)$
$µ_x={1 \over N_P}X^TP^T1$
$µ_y={1 \over N_P}Y^TP1$

위의 $t$에 관한 식을 Q에 대입하면 아래와 같습니다.

$Q = {1 \over {2 \sigma^2}}[tr(\hat X^Td(P^T1))\hat X - 2s\space tr(\hat X P^T \hat Y R^T)+s^2tr(\hat Y^Td(P1))\hat Y]+{N_PD \over 2}log \sigma^2$
$\hat X = X - 1 µ_x^T$
$\hat Y = Y - 1 µ_y^T$

한편, 위 식을 $R$에 대해서 최적화하면 $-tr(\hat X P^T \hat Y R^T)$을 최소화하는 문제로 환원되고 이는 곧 $tr((\hat X P^T \hat Y)^T R)$을 최대화 하는 문제입니다.

$max \space tr(A^TR), A=\hat X P^T \hat Y, \space s.t. \space R^TR=I, det(R)=1$
$R = UCV^T, \space where \space USSV^T = svd(\hat X^T P^T \hat Y), C = d(1, .., 1, det(UV^T))$

그 뒤의 $Q$의 다른 변수들에 대해서 최적화를 진행하면 아래와 같은 알고리즘을 생성할 수 있습니다.

Unsupervised 3D Link Segmentation of Articulated Objects With a Mixture of Coherent Point Drift

1. Problem Formulation

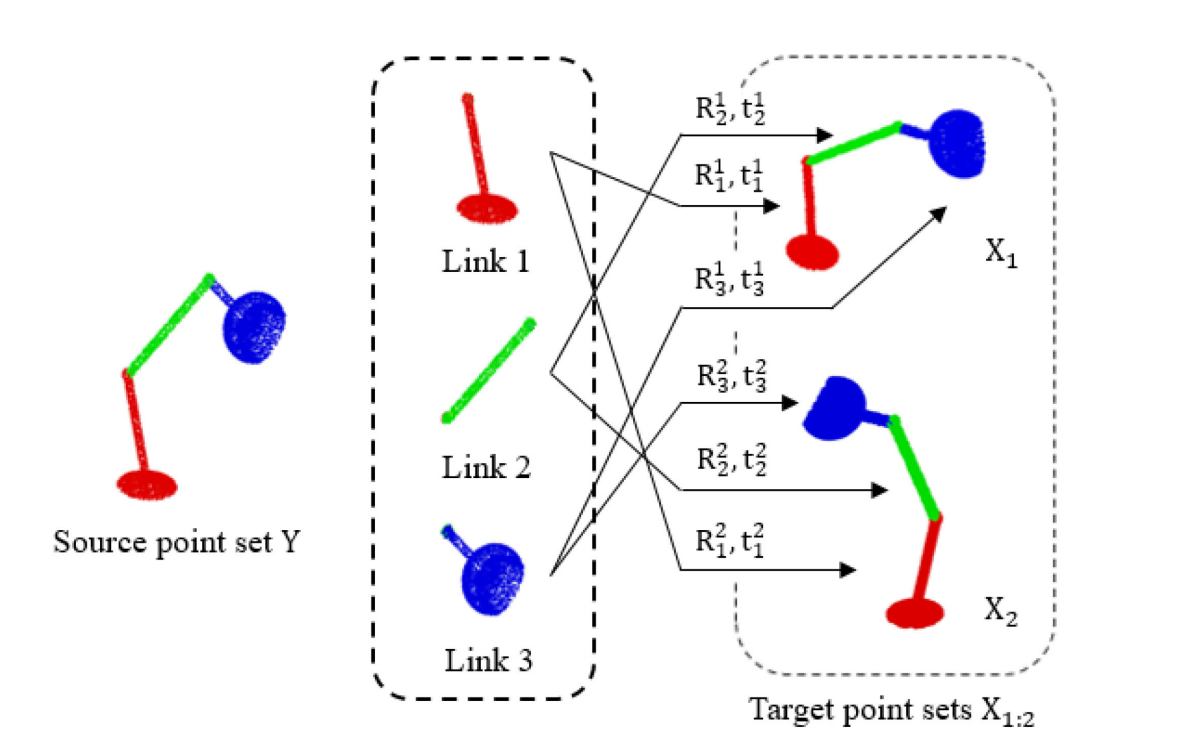
우리의 모델의 목적은 point set의 최적 decomposition과 probability density로 표현되는 transformation을 찾는 것입니다. 위의 그림에서 볼 수 있듯이 CPD에서의 formulation과 비슷하게 Y는 source point set을 나타냅니다. Y의 point set은 K개의 link로 분리가 되어 target point sets X와 매칭이 됩니다. 이때 각 link는 rigid transformation을 통해서 변환되도록 강제합니다.

$S$: target point sets의 개수
$K$: decompose 될 link의 개수
$N$: target point set를 구성하는 point의 개수
$M$: source point set를 구성하는 point의 개수
$X_{1:S}$: target point sets
$Y$: source point set (GMM centroids)
$R_{sk}, R_{1:S, 1:K}$: k번째 link가 s번째 link로 matching 되는 rotation
$t_{sk}, t_{1:S, 1:K}$: k번째 link가 s번째 link로 matching 되는 translation
$\Pi \space (M × K$ matrix) , $\pi_{ij}$: $\pi_{ij}$는 i번째 source point가 j번째 link에 속할 확률입니다.
$\pi_{ij} = p(Z_i = j|y_i)$: $Z_i$는 latent variable

2. Expectation of the complete negative log-likelihood function

$y_m$과 $Z_m=k$가 주어졌을 때, GMM centroid에 기반한 분포에 의해서 $x_{sn}$이 생성될 확률은 아래와 같습니다.

$p(x_{sn}|y_m,Z_m=k,\theta) = {1 \over (2 \pi \sigma^2)^{D/2}} exp(-{1 \over 2}({|x_{sn}-R_{sk}y_m-t_{sk}| \over \sigma})^2) = g(s_{sn}, R_{sk}y_m+t_{sk},\sigma^2)$

여기서, 우리가 최적화 해야 할 objective(Expectation of the complete negative log-likelihood) function은 아래와 같이 표현 될 수 있습니다.

$Q(\theta|\hat\theta) = E_{Z|X_{1:S}, Y, \hat \theta}[logp(X_{1:S}, Y,Z|\theta)]$

3. E-step and M-step

(1) E-step
아래는 $x_{sn}, y_m$이 주어졌을 때, $Z_m=k$일 responsibility를 나타냅니다.

$\hat T_{snmk}=p(Z_m=k|x_{sn},y_m;\hat \theta)={\hat \pi_{mj}g(s_{sn}, \hat R_{sk}y_m+t_{sk},\hat \sigma^2) \over \sum_{j=1}^{K} \hat \pi_{mj}g(s_{sn}, \hat R_{sj}y_m+t_{sj},\hat \sigma^2)}$

위를 활용해 objective function을 재정리하면 아래와 같습니다.

$Q(\theta|\hat \theta) = \sum_{snmk}\hat T_{snmk}[log({1 \over M})+log \pi_{mk}-{D \over 2}log(2\pi\sigma^2)-{1 \over 2}({|x_{sn}-R_{sk}y_m-t_{sk}| \over \sigma})^2]$

(2) M-step
objective function을 $t_{sk}$에 대해서 최적화를 진행해주면 아래의 식을 얻을 수 있습니다.

$t_{sk} = μ_{skx} − R-{sk}μ_{sky}$
$μ_{skx} = {\sum_{nm} \hat T_{snmk} x_{sn} \over \sum_{nm} \hat T_{snmk}}$
$μ_{sky} = {\sum_{nm} \hat T_{snmk} y_{m} \over \sum_{nm} \hat T_{snmk}}$

위의 식을 objective function에 대입해 $t_{sk}$에 대한 dependency를 없애주고 각 variables에 대해서 최적화를 진행해줍니다.
이때 $\sigma$는 아래와 같은 해를 얻을 수 있습니다.

$\sigma^2={\sum_{snmk \hat T_{snmk} (x_{sn}-R_{sk}y_m-t_{sk})^2} \over \sum_{snmk \hat T_{snmk}D}}$

또, $R_{sk}$에 대해서는 아래의 optimal problem을 얻을 수 있습니다.

$R_{sk}=argmax_{R_{sk}}tr(A_{sk}^TR_{sk}), A_{sk}=X_{sk}^T \hat T_{sk}^T Y_{sk}$
$X_{sk} = X_s-1 \mu_{skx}$
$Y_{sk} = Y-1 \mu_{sky}$

마지막으로 $\pi_{mk}$에 대해서 아래의 식을 얻을 수 있습니다.

$\pi = argmax_\pi \sum_{snmk}\hat T_{snmk}log \pi_{mk} \space s.t. \sum_k \pi_{mk}=1$

더 나아가, objective function에 아래의 regularization term을 더해줍니다. 우리는 KL divergence를 활용해서 가까운 point 끼기의 $\pi$가 비슷해질 수 있도록 규제합니다. 이때, 추가된 항은 $\pi$만 영향을 줍니다.

$R(\Pi) = - \sum_{i,j=1}^{M}w_{ij}D_{KL}(\pi_i||\pi_j) ≈ -2 \sum_{i=1, i \ne m}^{M}w_{im}\pi_{ik}log({\pi_{ik} \over \pi_{mk}})$

위의 모든 최적화 작업을 취합해서 알고리즘을 형성하면 아래의 pipeline으로 정리할 수 있습니다.

마치며,

non-rigid transformation에 대해서는 아직 살펴보지 않았지만 당장 필요한 rigid transformation에 대한 학습은 적당히 마무리했습니다. EM과 몇몇 선형대수학, 확률론의 지식을 되짚어가며 의미 있는 시간을 보냈습니다. 앞으로는 이와 관련된 code review를 진행하고 어떻게 하면 저의 연구에 쓸모 있게 변형해낼 수 있을지 고민하고 또 고민하는 것입니다. 번뜩이는 아이디어가 떠오르면 좋겠네요. 다음에 더 fancy 한 생각들로 찾아뵙겠습니다!