Notation

나두진·2021년 8월 9일
latexnotation
0

Deep learning." An MIT Press book. (2015)

목록 보기
1/2

Notation

this section provides a concise reference describing the notation used throughout this book.

if you are unfamiliar with any of the corresponding mathematical concepts, we describe most of these ideas in chapters 2-4.

Numbers and Arrays

aa

A scalar (integer or real)

a\textbf{a}

A Vector

A\textbf{A}

A matrix

A\Alpha

A tensor

InI_n

Identity matrix with n rows and n columns

e(i)e^{(i)}

Standard basis vector [0, . . . ,0,1,0, . . . ,0] with a 1 at position i

diag(a)diag(\textbf{a})

a square, diagonal matrix with diagonal entries given by 'a'

Sets and Graphs

A\mathbb{A}

'A' set

R\mathbb{R}

The set of real numbers

{0,1}

The set containing 0 and 1

{0,1.....,n}

The set of all integers between 0 and n

[a,b][a,b]

The real interval including a and b

(a,b](a,b]

The real interval excluding a but including b

A/B\mathbb{A}/\mathbb{B}

Set subtraction, i.e., the set containing the elements of A that are not in B

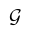
A graph

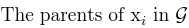
Indexing

aia_i

Elements i of vector 'a' , with indexing starting at 1

a−ia_-i

All elements of vector 'a' except for element i

AijA_{ij}

Elements i,j of matrix A

Ai,:A_{i,:}

Row i of matrix A

A:,iA_{:,i}

Column i of matrix A

Ai,j,kA_{i,j,k}

Elements (i,j,k) of a 3-D tensor A

Linear Algebra operations

ATA^T

Transpose of matrix A

A+A^+

Moore-Penrose pseudoinverse of A

A⨀BA \bigodot B

Element-wise (Hadamard) product of A and B

det(A)det(A)

Determinant of A

Calculus

dydx\frac{dy}{dx}

Derivative of y with respect to x

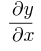
Partial derivative of y with respect to x

▽xy\bigtriangledown_xy

Gradient of y with respect to x

▽Xy\bigtriangledown_Xy

Matrix derivatives of y with respect to X

▽xy\bigtriangledown\textbf{x}y

Tensor containing derivatives of y with respect to X

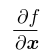
Jacobian matrix

J∈Rm∗noff:R→RmJ \in \mathbb{R}^{m * n} of \\ f :\mathbb{R} \rightarrow \mathbb{R}^m
∫f(x)dx\int \mathrm{f}(x)dx

define integral over the entire domain of x

∫Sf(x)dx\int _\mathbb{S} f(x)dx

Definite integral with respect to x over the set S

Probability and Information Theory

a⊥ba\perp b

The random variables a and b are independent

a⊥b∣ca\perp b \mid c

They are conditionally independent given c\

P(a)P(a)

a probability distribution over a discrete variable

p(a)p(a)

A probability distribution over a continuous variable, or over a variable whose type has not been specified

a∼Pa \sim P

Random variable a has distribution P

Ex∼P[f(x)]orEf(x)\mathbb{E}_{x \sim P}[f(x)] or \mathbb{E}f(x)

Expectation of f(x) with respect to P(x)

Var(f(x))Var(f(x))

Variance of f(x) under P(x)

Cov(f(x),g(x))Cov(f(x),g(x))

Covariance of f(x) and g(x) under P(x)

H(x)H(x)

Shannon entropy of the random variable x

DKL(P)∥QD_{KL}(P)\parallel Q

Kullback-Leibler divergence of P and Q

N(x;u,∑)\mathcal{N} (x;u,\sum)

Gaussian distribution over x with mean µ and covariance Σ

Function

f:A→Bf:\mathbb{A} \to \mathbb{B}

The function f with domain A and range B

f∘gf \circ g

Composition of the functions f and g

f(x;θ)f(x;\theta)

A function of x parametrized by theta, (Sometimes we write f(x) and omit the argument theta to lighten notation)

logxlogx

Natural logarithm of x

α(x)\alpha(x)

Logistic sigmoid,

11+exp(−x)\frac{1}{1+exp(-x)}

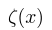
Softplus, log(1_exp(x))

∥x∥p\parallel x \parallel_{p}

∥x∥\parallel x \parallel

x+x^+

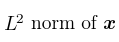
Positive part of x , i.e., max(0,x)

1condition1_{condition}

is 1 if the condition is true, 0 otherwise

Datasets and Distributions

PdataP_{data}

The data generating distribution

P^data\hat{P}_{data}

The empirical distribution defined by the training set

X\mathbb{X}

A set of training examples

xix^{i}

The i-th example (input) from a dataset

yioryiy^{i} or y^{i}

The target associated with x^{i} for supervised learning

XX

The m x n matrix with input example x^{i} in row Xi:

profile
나두진
jph
다음 포스트

Linear Algebra

0개의 댓글