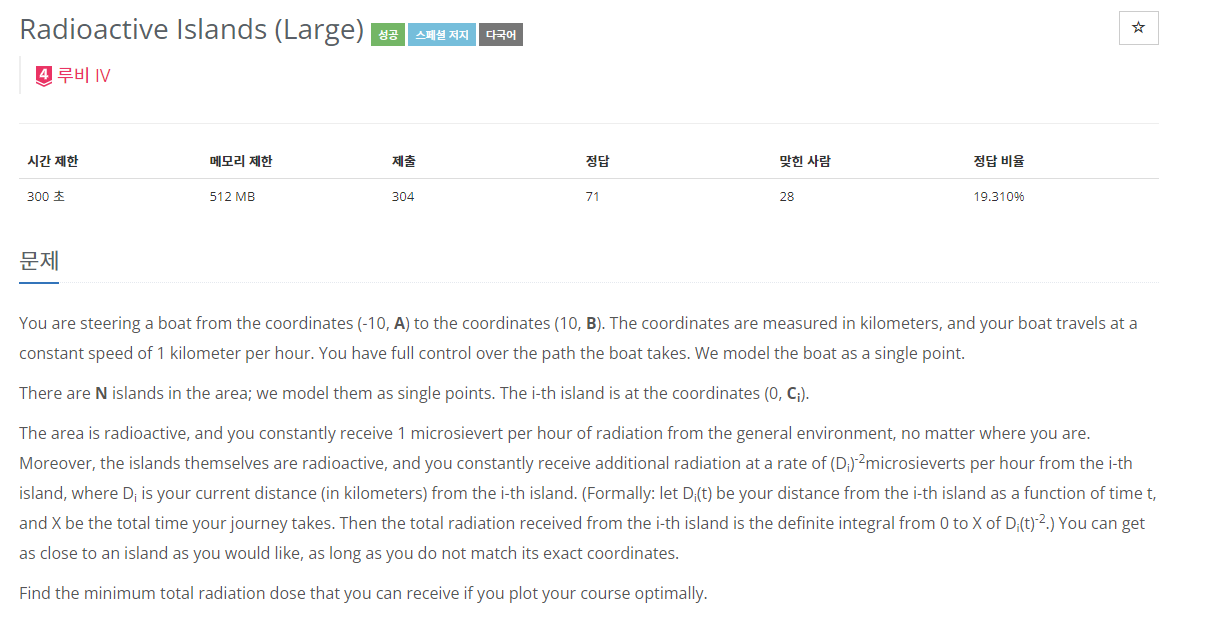
우선 문제를 한 번 살펴봅시다.
- 에서 보트가 출발하며, 에 도착해야 한다.
- 현재 보트와 섬과의 거리를 이라고 할 때, 매 초마다 의 손상을 입는다.
- 어느 위치에 있든 씩의 기본 손상을 입는다.
- 이 때, 최소한의 손상을 받는 경로로 목적지에 도착했을 때 입은 손상의 정도를 구해야 한다.
출발지에서 목적지까지의 단순 최단 경로로 이동하다가는 섬에서 나오는 방사능에 휩싸일 것이고, 그렇다고 너무 크게 돌아 목적지로 향하다가는 기본 방사선을 계속 받아 많은 피해가 누적될 것입니다.
그렇기에, 우리는 적절한 경로를 찾아야 합니다.
이 상황을 적분식으로 최적화 하여 표현해보도록 합시다.
경로 곡선의 길이는 아래의 식으로 구해낼 수 있습니다.
섬으로부터 받는 방사선의 양을 계산하기 위해선, 각 구간 마다 받는 방사선에 해당 구간을 지나는 시간을 고려합니다.
이 때, 우리는 두 함수의 합을 최적화시키기 위해 오일러-라그랑주 방정식을 사용할 것입니다.
함수 가 경계값 조건인 를 만족하며 다음과 같이 주어지는 범함수 를 최대 혹은 최소로 만든다고 할 때,
( 이 때, 는 연속적인 편미분 값을 가진다고 가정합니다. )
만일 가 상대 범함수를 최대, 최소로 한다고 하면, 에 매우 작은 변화를 가했을 때 의 값이 늘거나 의 값이 줄어들 수 있습니다.
그 때 에 매우 작은 변화를 주는 함수 를 도입합시다. ( 이 때, 는 을 만족하는 미분 가능한 함수입니다. )
이제 대신 를 넣은 는 다음과 같은 함수가 될 것입니다.
이제 를 에 대해 미분한 전미분을 구하면,
전미분의 정리에서 다음과 같은 식이 나오며,
이를 정리합니다.
만약 이라면 입니다. 그리고 이 때 가 를 극값으로 만드는 부분이므로, 입니다.
이를 수식으로 써 봅시다.
두 번째 항에 부분적분을 해줍니다.
여기서 의 경계값 조건을 이용해줍니다.
여기서 변분법의 기본 정리를 적용시켜줍니다.
이로써 위와 같은 오일러-라그랑주 방정식을 얻었습니다. 이를 적절히 이항 시켜주고 구한 식을 앞서 구한 함수에 적용시켜 줍니다.
그러면 아래와 같은 식을 얻을 수 있습니다.
이를 정리하여 를 로 나타내봅시다.
위에서 구한 식을 바탕으로 의 초기값으로 의 값을 구할 수 있게 되었습니다. 와 의 초기값은 주어지므로 의 초기값만 찾으면 됩니다.
의 초기값을 조정하는 방법으로는 이분 탐색이 있습니다.
섬 위를 지나는 경로와 섬 아래를 지나는 경로로 하나씩 잡은 뒤 위쪽의 최적 경로와 아래쪽의 최적 경로 둘을 비교하여 더 낮은 피해를 입는 경로가 최적의 경로로 정해질 것입니다.
섬이 두 개인 Large 문제의 경우, 문제의 해결 방법 자체는 같으나 적분식의 변환이 필요합니다.
또한 위쪽의 섬 위로 돌아가는 경로, 아래쪽의 섬 아래로 돌아가는 경로, 두 섬의 중앙으로 지나가는 경로 이 세 경로를 비교해 보아야 합니다.
아래는 저의 완성된 코드입니다.
def binarySearch(x, y, l, r):
ret = float('inf')
while abs(r - l) / 2 > 1.1920929e-7:
mid = (l + r) / 2
temp = calc(-10, x, mid)
ret = temp[0]
if temp[1] < y:
l = mid
else:
r = mid
return ret
def calc(x, y, pos):
ret = 0
for _ in range(2000):
if y > 13 or y < -13:
return [float('inf'), y]
ret += (yFunction(x, y) + 1) * (pos ** 2 + 1) ** 0.5 / 100
x += 0.01
y += pos / 100
pos += EularLagrangeEquation(x, y, pos) / 100
return [ret, y]
def yFunction(x, y):
ret = 0
for i in islands:
d = x ** 2 + (y - i) ** 2
if d < 1.1920929e-7:
return float('inf')
ret += d ** -1
return ret
def EularLagrangeEquation(x, y, pos):
temp = pos ** 2 + 1
ret = 1
p1 = p2 = 0
for i in islands:
d = x ** 2 + (y - i) ** 2
ret += d ** -1
p1 += (y - i) / d ** 2
p2 += (x + (y - i) * pos) / d ** 2
return temp * (pos * p2 - temp * p1) * 2 / ret
for i in range(int(input())):
n, a, b = map(float, input().split())
islands = list(map(float, input().split()))
slopes = sorted([-2, 2] + [(i - a) / 10 for i in islands])
result = float('inf')
for j in range(len(slopes) - 1):
temp = binarySearch(a, b, slopes[j], slopes[j + 1])
if result > temp:
result = temp
print(f'Case #{i + 1}: {round(result, 2)}')