[자료구조]Tree에 관하여

Goal

• Tree가 무엇인지 설명할 수 있다.
• Tree가 어디에 사용되는지 알 수 있다.

Tree란 무엇인가?

• 비순차적 자료 구조
• 계층 구조(hierarchical structure)를 추상화한 모델

Tree는 다들 아시다시피 '나무' 입니다.
나무는 뿌리에서 시작되어 가지 -> 잎이 나오죠! 이 자료구조 또한 같습니다.

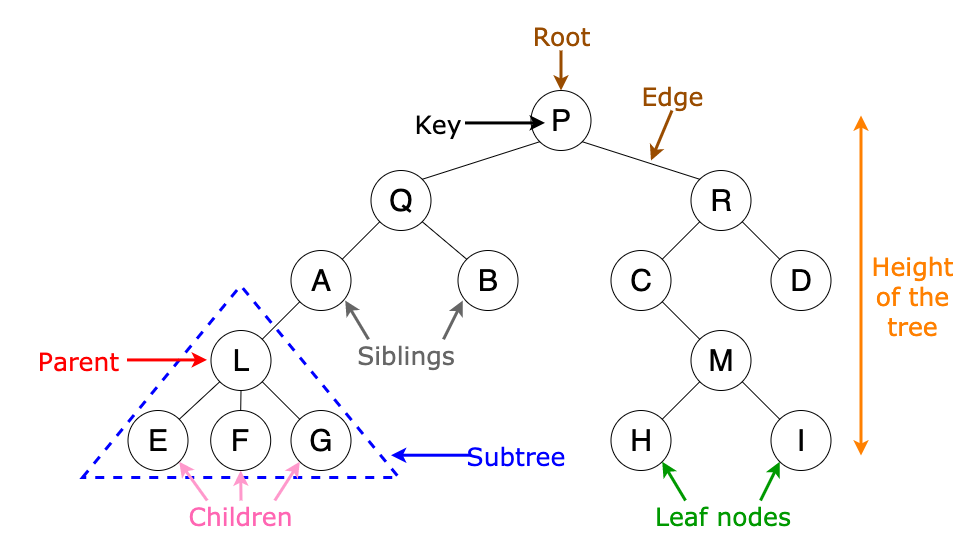
맨 상단에 뿌리(Root) 에서 시작되어 가지(Edge) 를 뻗으며 커지고 가지 끝에는
잎(Leaf) 이 나옵니다. 각각의 동그라미는 Node 라고 부르죠!
깊이(depth) 는 Root 부터 0으로 시작해 'P'의 depth는 0, 'Q' , 'R'의 depth는 1 처럼 1씩 증가합니다.

Tree는 어디에 쓸까요?

Tree는 다음과 같은 곳에 사용됩니다.

• File System
• DOM Tree
• 주소 체계 (like 부평구 삼산동)

이 외에도 정말 사용되는 곳이 많고, 사용하는 방법도 무궁무진합니다.
이진 탐색 트리, AVL트리, 레드-블랙 트리, 최소 비용 신장 트리, B-트리 등등..
종류도 정말 많죠.. 그래서 이번 주차에는 이진트리에 관해서만 알아보겠습니다. 😁

---

이진트리와 이진 탐색 트리

이진 트리(binary tree) 는 Tree 중 하나로 좌측과 우측만이 존재합니다.
즉, 각각의 노드는 최대 2개의 자식 노드만 가질 수 있습니다.

그렇다면 이진 탐색 트리(binary search tree) 는 무엇일까요 ?
이진 트리의 변형으로, 좌측이 더 작은 값을 들고 있는 것입니다!
그림과 함께 보시죠 !

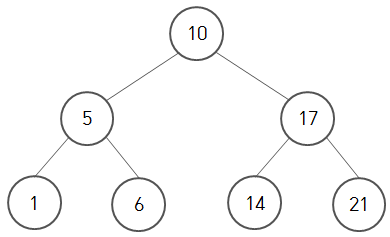
먼저 Tree에 '10' 이 들어왔습니다. 그 후에 트리에 '5'를 넣을 상황입니다.

그럼 5 < 10 이기 때문에!
즉, 들어갈 값이 현재 node보다 작기 때문에 '5'는 left에 들어가게 되는 것이죠 !
그 후에 '17'을 넣으면 당연히 10 < 17 이기 때문에 우측에 들어가겠죠 !?

그럼 이 다음에 '6'을 넣어 보겠습니다.
일단 6 < 10 이기 때문에 당연히 left에 들어가야 합니다.

앗 그런데 ! ⛔

이미 5가 자리를 차지하고 있죠! 그러면 '6'을 다시 '5'와 새롭게 비교합니다.
그럼 5 < 6 이기 때문에 5의 right에 들어가게 되는 것이죠.

굉장히 Linked List와 비슷하네요..! pointer가 두 개인 Linked List 느낌..

---

이진 탐색 트리 구현하기

// 1. 현재보다 큰지 작은지 보고
// 2. 값을 넣을 거야!
// 2-1. 작으면 왼쪽
// 2-2. 크면 오른쪽
// 3. 근데 만약에 넣을 자리에 node가 있다면 거기 있는 노드를 현재 노드로 바꿀 거야
// 4. 그리고 다시 1번을 실행할 거야
// 재귀함수를 쓰면 될까?

class Node {
  constructor(key) {
    this.key = key;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  // 새로운 키를 삽입
  insert(key) {
    const newNode = new Node(key);

    if (this.root === null) {
      this.root = newNode;
      return;
    }

    function insertNode(node, newNode) {
      if (newNode.key < node.key) {
        node.left === null ? (node.left = newNode) : insertNode(node.left, newNode);
      } else {
        node.right === null ? (node.right = newNode) : insertNode(node.right, newNode);
      }
    }

    insertNode(this.root, newNode);
  }

  // 해당 키가 있는지 없는지 반환 => boolean
  search(key) {
    let result;
    function searchNode(node, key) {
      if (node === null) return (result = false);

      if (node.key === key) {
        return (result = node);
      } else if (key < node.key) {
        searchNode(node.left, key);
      } else {
        searchNode(node.right, key);
      }
    }

    searchNode(this.root, key);
    return result;
  }

  // tree의 최솟값
  min() {
    //
    let result;

    function searchMinValue(node) {
      if (node === null) throw new Error("root가 없짜나!!!!!!!!!!");

      if (node.left === null) {
        result = node.key;
        return;
      }

      if (node.left !== null) searchMinValue(node.left);
    }

    searchMinValue(this.root);
    return result;
  }

  // tree의 최댓값
  max() {
    //
    let result;

    function searchMinValue(node) {
      if (node === null) throw new Error("root가 없짜나!!!!!!!!!!");

      if (node.right === null) {
        result = node.key;
        return;
      }

      if (node.right !== null) searchMinValue(node.right);
    }

    searchMinValue(this.root);
    return result;
  }
}

---