빅오(big-O) 표기법이란?

본 글은 POCU COMP1000: 소프트웨어 공학용 수학 강의 를 듣고 스스로 정리한 내용입니다.

들어가기 전에

지금 작성하신 코드, 빅오 표기법으로 어떻게 되요?
실행 복잡도가 어떻게 되요?
시간 복잡도가 어떻게 되요?

기술 면접에 불려가 코드를 작성하면 면접관들에게 자주 듣는 질문이라고 한다. 여기서 빅오가 뭐에요? 하면 탈락 확정인 거고.. 대답도 잘 해야 한다.

이러한 질문을 하는 이유는 스스로 작성한 코드가 어느 정도 속도로 돌아가는지 알고있는지를 물어보는 것이다. 프로그래머라면 내가 작성하는 코드가 얼마나 느린지 알 수 있어야 하고,항상 더 효율적인 코드를 작성하기 위해서 고민하고 또 고민해야 한다고 생각한다.

이러한 관점에서 이번 포스팅에서는 점근표기법 (빅오 표기법)에 대해서 자세히 알아보려고 한다.

점근 표기법 (asymptotic notation)

점근 표기법은 우리가 작성한 코드, 더 정확히는 알고리즘의 성능을 측정하기 위한 척도이다. 이 점근 표기법을 통해서 어떤 함수가 증가하는 모습을 다른 함수와 비교 할 수 있고 더 나아가 알고리즘의 복잡도를 논하거나 단순화시킬 때 사용할 수 있다. 대표적인 표기법은 아래와 같다.

• 대표적인 표기법
  • 대문자 O 표기법 (big-O)
  • 소문자 o 표기법
  • 대문자 오메가 표기법
  • 소문자 오메가 표기법
  • 대문자 세타 표기법

컴퓨터 공학에서는 주로 대문자 O 표기법 (big-O)를 사용한다.

컴퓨터 공학에서의 빅오 표기법

• 대문자 O를 이용해 표기
• 알고리즘을 분류하기 위해 사용
• $O(1), O(log n), O(n), O(nlog n), O(n2), O(n!)$
• 여기서 O는 'order of the function' (대략 그 함수 정도)를 의미
  • 이 의미에 대해서는 뒷부분에 자세히 살펴보도록 하자!

어떤 기준으로 분류할까?

입력 데이터가 많아짐에 따라 실행시간과 필요한 공간이 얼마나 늘어나는지 측정한다. 여기서 실행 시간은 시간복잡도를 의미하는데, 이는 실행해야 하는 알고리즘의 단계수로 나타낸다. 공간복잡도는 사용하는 메모리의 양을 나타낸다. 우리가 흔히 말하는 알고리즘에서 주로 신경쓰는 부분은 시간 복잡도이다.

빅오 표기법은 단항식

빅오 표기법은 계수가 없는 단항식으로 표현된다.

왜 그럴까??

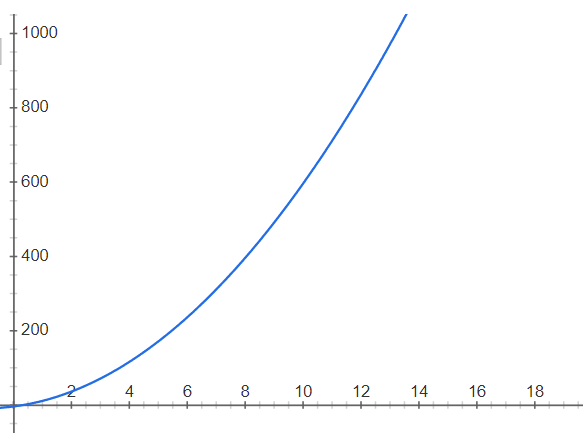
실행 시간 T(n)이 다음과 같은 알고리즘이 있다고 가정을 해보자.

$T(n) = 5n^2 + 10n - 4$

여기서 살펴보고 싶은 것은 n (입력 데이터)이 증가할 때 $5n^2$ / $10n$ / $4$ 이 중에 어떤 것이 실행시간에 가장 결정적인 영향을 미치냐?는 것이다.

상식적으로 봐도 가장 높은 차항인 $5n^2$이 가장 큰 영향을 미치는 것으로 보인다.

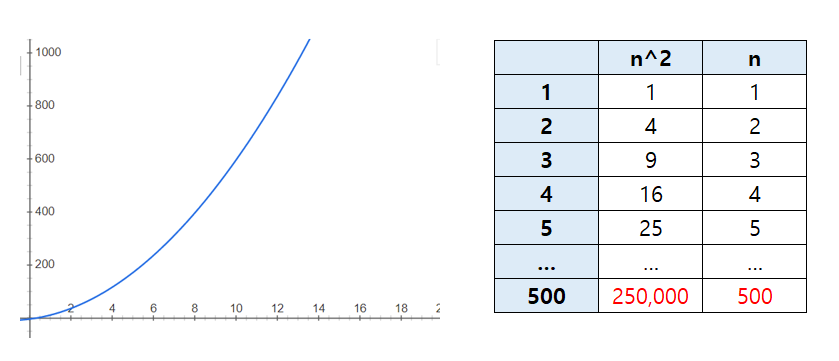
아래의 표를 보자

n (입력 데이터 수)가 1일 때 $n^2(1)$과 $n(1)$은 같다.
$n = 2$일 때, $n^2 (4)$는 $n(2)$의 2배 만큼 값이 커진다.
$n = 3$일 때, $n^2$은 $n$의 3배
...
n=500일 때, $n^2$은 $n$보다 무려 500배나 커 진다.

n이 증가하면 증가할 수록 $n^2$과 $n$의 격차가 크게 벌어짐을 알 수 있다.

즉, $n^2$이 실행시간에 결정적인 영향을 미치고 있다는 것을 (n은 크게 의미가 없는 수치임을) 알 수 있다.

계수도 크게 의미 없다

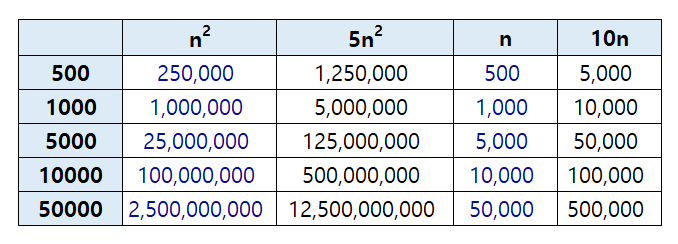
먼저 $n^2$ 과 $5n^2$을 보자.

n이 500일 때 $n^2$은 250,000, $5n^2$은 1,250,000이다.
자릿수 하나 늘어났지만, $n$과 $n^2$의 차이는 그렇게 크지 않다.

그러면 데이터를 확 늘려서 $n$이 50000일 때는 어떨까?
$n^2$은 250,000,000, $5n^2$은 1,250,000,000이다.
역시 자릿수 하나는 늘었지만 이 둘의 차이는 그렇게 크지 않다.

입력 데이터가 아무리 늘어나도 언제나 5배 차이인 것이다.

n과 /10n도 마찬가지로 입력 데이터가 아무리 증가해도 언제나 10배 차이밖에 나지 않는다.

때문에, 실제로 계수보다 항의 차수가 하나 올라가는 게 훨씬 더 큰 영향을 미침을 알 수 있다.

마찬가지 이유로 상수도 의미가 없음을 알 수 있다.

따라서, T(n)을 빅오 표기법으로 표현하면

$T(n) = 5n^2 + 10n - 4$

=> $T(n) = O(n^2)$

앞에서 O는 '대략 어느 정도'라고 표현을 했다.
T(n)은 대략 O($n^2$)정도 라고 말할 수 있다.

빅오 표기법에서의 곱

두 함수 f1, f2의 실행 복잡도가 각각 $f1 = O(g1), f2 = O(g2)$일 때, 이 두 함수를 곱한 것의 실행 복잡도는 다음과 같다

• $f1f2 = O(g1g2)$
  • 예) $f1 = O(n), f2 = O(n^2)$일 때, f1f2의 시간 복잡도
    => $f1f2 = O(g1g2) = O(n * n^2) = O(n^3)$

빅오 표기법에서의 합

두 함수 f1, f2의 실행 복잡도가 각각 $f1 = O(g1), f2 = O(g2)$일 때, 이 두 함수를 합한 것의 실행 복잡도는 다음과 같다

• $f1f2 = O(MAX(g1,g2))$
  • 예) $f1 = O(n), f2 = O(n^2)$일 때, $f1 + f2$의 시간 복잡도
    => $f1 + f2 = O(MAX(n, n^2)) = O(n^2)$

복잡해 보이는 예

$f(n) = 7log n + 3(log n)^4 + 10n^2 + 5n^3$

위 함수를 빅오표기법으로 표현하면?
=> O ($n^3$)

이렇게 복잡해 보이는 함수도 최고차항만 구하면 쉽게 간략화 가능 하다!

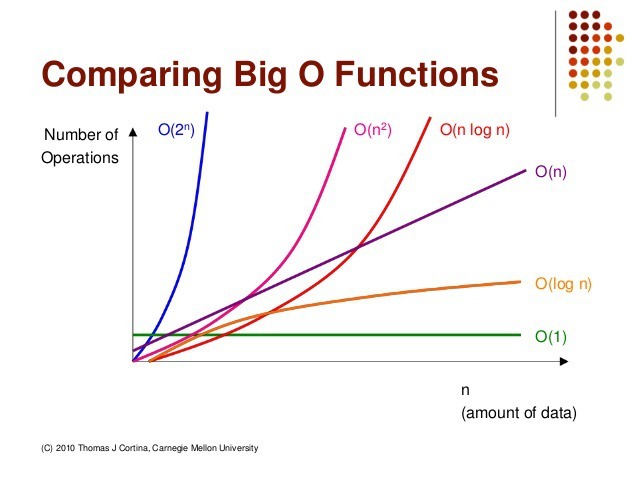
흔히 볼 수 있는 O 표기법의 크기 비교

작음 $O(1) < O(log n) < O(n) < O (n log n) < O(n^2) < O(2^n)$ 큼

O표기법 예 (C#)

O(1)예

• 반복문이 없으면 기본적으로 O(1)

string getUserName(int index)
{
    return mUsers[index];
}

O(log n) 예

• 분할정복 알고리즘 이진탐색이 대표적인 예
  • 봐야 할 데이터를 반씩 줄여나가면서 탐색하는 방식

public static bool BinarySearchRecursive(int[] nums, int val, int left, int right)
{
    if (min > max)
    {
        return false;
    }
    
    int mid = (left + right) / 2;

    if (val == nums[mid]
    {
        return true;
    }
    else if (val < nums[mid])
    {
        return BinarySearchRecursive(nums, val, left, mid - 1);
    }
    else
    {
        return BinarySearchRecursive(nums, val, mid + 1, right);
    }
}

O(n)의 예

• for문 하나 있을 때

uint sumEven(uint n)
{
    uint sum = 0;
    
    for (uint i = 1; i <= n; ++i)
    {
        sum += 2 * i;
    }
    
    return sum;
}

O($n^2$)의 예

• 중첩 for문

void bubbleSort(int[] nums) {
    const uint length = nums.length;

    for (uint i = 0; i < length; ++i)
    {
        for (uint j = 0; j < length - 1; ++j)
        {
            if (nums[j] < nums[j + 1])
            {
                nums[j] ^= nums[j + 1];
                nums[j + 1] ^= nums[j];
                nums[j] ^= nums[j + 1];
            }
        }
    }
}

O($2^n$) 예

• 피보나치 수열

public static int FibonacciRecursive(uint number)
{
    if (number == 0)
    {
        return 0;
    }
    
    if (number == 1)
    {
        return 1;
    }
    
    return FibonacciRecursive(number - 2) + FibonacciRecursive(number - 1);
}

O(n!) 예

• 외판원 (traveling salesman)문제가 가장 대표적
  • 여러 도시를 돌아다녀야 하는 외판원
  • 모든 도시를 단 한 번만 방문한 뒤 다시 첫 도시로 돌아오는 경로를 찾는 문제
  • 그래프 이론을 정리할 때 다룰 예정

정리

이번 포스팅에서는 빅오 표기법에 대해서 알아보았다.

내가 작성한 코드가 얼마나 느리게 돌아가는지, 어떻게 하면 속도를 줄여나갈 수 있을지 항상 생각하면서 코드를 작성하는 습관을 들이도록 하자..!