💬 문제
문제 난이도: Lv.3
문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/84021
문제 설명
테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈 공간(빈칸)에 적절히 올려놓으려고 한다.
게임 보드와 테이블은 모두 각 칸이 1*1 크기인 정사각형 격자 모양이다.
이때 다음 규칙에 따라 테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈칸에 채우면 된다.
규칙에 맞게 최대한 많은 퍼즐 조각을 채워 넣을 경우, 총 몇 칸을 채울 수 있는지 반환하라.
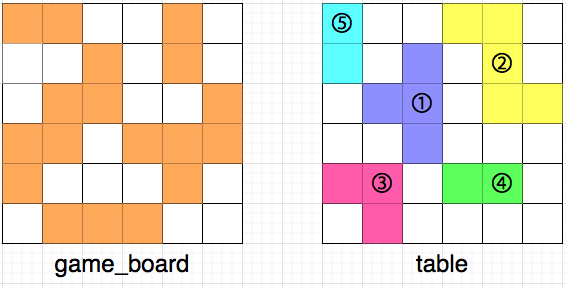
[규칙]
1. 조각은 한 번에 하나씩 채워 넣는다.
2. 조각을 회전시킬 수 없다.
3. 조각을 뒤집을 수 없다.
4. 게임 보드에 새로 채워 넣은 퍼즐 조각과 인접한 칸이 비어있으면 안된다.
❗️접근 방법
문제 이해
규칙을 통해 문제의 조건을 파악하자.
여러 개의 조각으로 빈칸을 채울 수는 없다. 즉, 조각을 회전해서든 빈칸에 딱 맞게 들어가는 경우를 찾아야 한다.
game_board의 빈칸, table의 조각을 표현하는 방법
bfs를 사용해서 한 빈칸(혹은 조각)을 이루는 좌표들을 구할 수 있다.
이렇게 구한 좌표들을 원소로 갖는 2차원 배열이 한 빈칸(혹은 조각)을 의미한다.
나는 (y, x)좌표를 정수(y*N+x)로 바꿔서 저장했다.
예를 들어 위 그림에서 1번 조각은 [8, 13, 14, 20]으로 표현할 수 있다.
2차원 배열을 90도씩 회전하기
위 방법으로 조각을 저장해두면 90도로 회전시켰을 경우를 표현하기 어려워진다.
따라서 조각을 포함하는 가장 작은 직사각형을 만들고, 조각을 1로 아닌 부분을 0으로 표시한 2차원 배열을 만든다.
그리고 spin 함수를 정의해서 90도로 회전한 결과물을 만들어 낸다.
빈칸과 조각이 '딱 맞는지' 비교하기
빈칸도 조각처럼, 빈칸을 포함하는 가장 작은 직사각형을 만들고, 빈칸을 1로 아닌 부분을 0으로 표시한 2차원 배열을 만들어 저장해둔다.
그리고 한 조각에 대해 만들어질 수 있는 최대 4가지 경우(90도씩 회전 4번한 경우) 중 너비(가로), 높이(세로)가 같은 경우에, 두 2차원 배열의 각 원소가 값이 모두 같다면 '딱 맞는다'고 할 수 있다.
코드
from collections import deque, defaultdict
blocks = defaultdict(list) # key: 빈칸의 크기, value: 그 크기의 빈칸을 가장 작은 직사각형으로 표현한 2차원 배열
puzzles = defaultdict(list) # key: 조각의 크기, value: 그 크기의 조각을 가장 작은 직사각형으로 표현한 2차원 배열
def bfs(N,game_board, y, x, flag):
queue = deque([[y, x]])
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
temp = []
while queue:
y, x = queue.popleft()
if game_board[y][x] == empty:
game_board[y][x] = 1-empty
temp.append(y*N+x)
for i in range(4):
nx = dx[i] + x
ny = dy[i] + y
if 0<=nx<N and 0<=ny<N:
if game_board[ny][nx] == empty:
queue.append([ny, nx])
matrix = makeSquare(temp, N) # --- 1️⃣ 조각(혹은 빈칸)을 포함하는 가장 작은 사각형, 조각(빈칸)에는 1을 그렇지 않은 곳에는 0을 채워놓음.
# 2️⃣ game_board는 0으로 빈칸을 나타내고, table은 1로 조각을 나타내므로
# flag 0과 1을 나타냄.
if flag == 0:
blocks[len(temp)].append(matrix)
else:
puzzles[len(temp)].append(matrix)
def makeSquare(arr, N):
minV = [N, N] #x좌표, y좌표
maxV = [0, 0] #x좌표, y좌표
for elem in arr:
y, x = elem // N, elem % N
minV[0] = min(minV[0], x)
minV[1] = min(minV[1], y)
maxV[0] = max(maxV[0], x)
maxV[1] = max(maxV[1], y)
# 3️⃣ 가로: 가장 작은 x좌표와 큰 x좌표 간 거리
# 4️⃣ 세로: 가장 작은 y좌표와 큰 y좌표 간 거리
width = maxV[0] - minV[0] + 1
height = maxV[1] - minV[1] + 1
matrix = [[0]*width for _ in range(height)]
for elem in arr:
y, x = elem // N, elem % N
matrix[y-minV[1]][x-minV[0]] = 1
return matrix
def spin(arr, N):
result = []
# 5️⃣ 9도씩 4번 회전한 경우를 구하기(90 * 4 = 360)
for i in range(4):
n = len(arr)
m = len(arr[0])
new = [[0] * n for _ in range(m)]
for i in range(n):
for j in range(m):
new[j][n-i-1] = arr[i][j]
result.append(new)
arr = new
return result
def compare(arr1, arr2, N):
# 6️⃣ arr1: 빈칸, arr2: 조각, candidates: arr2를 회전해서 만들 수 있는 모든 경우의 수가 담김.
candidates = spin(arr2,N)
for candidate in candidates:
flag = True
# 7️⃣ 가로, 세로 크기가 모두 같아야 하고
if len(arr1) != len(candidate) or len(arr1[0]) != len(candidate[0]):
continue
for y in range(len(arr1)):
for x in range(len(arr1[0])):
# 8️⃣ 원소의 값이 모두 같아야 함.
if arr1[y][x] == candidate[y][x]:
continue
else:
flag = False
break
if flag:
return True
return False
def solution(game_board, table):
N = len(game_board)
# game_board에서 빈칸인 부분 찾기
for y in range(N):
for x in range(N):
if game_board[y][x] == 0:
bfs(N, game_board, y, x, 0)
# table에서 빈칸인 부분 찾기
for y in range(N):
for x in range(N):
if table[y][x] == 1:
bfs(N, table, y, x, 1)
cnt = 0
for key in blocks:
for arr1 in blocks[key]:
for arr2 in puzzles[key]:
if compare(arr1, arr2, N):
cnt += key # --- 9️⃣ key는 빈칸의 크기
puzzles[key].remove(arr2) # --- 🔟 사용한 조각 삭제
break
return cnt