[JS/Programmers] 12913. 땅따먹기

💬 문제

문제 난이도: Programmers Lv.2

문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/12913

❗️접근 방법

n행 4열로 구성된 2차원 배열이 주어진다.
한 행의 한 열만 지나갈 수 있고, 두 열을 연속으로 지나갈 수 없다.
각 셀에는 숫자가 적혀 있는데, 마지막 행에 도달했을 때 지나온 셀들의 합 중 최댓값을 반환해야 한다.

그리디는 아니구나!
1행 중 2열의 값이 5로 가장 크다고 가정하자. 이 때 2열을 거쳐 갔기 때문에 2행 2열은 거쳐갈 수 없다.
이때 2행 2열의 값이 100으로 큰 수라면, 1행에서 2열을 거쳐가면 안되었다는 것을 알 수 있다.

완전 탐색?
위의 조건을 만족하는 모든 경우의 수를 dfs를 사용해 구하면 결과적으로 최댓값을 알 수 있을 것이다.
하지만 이 방법은 시간초과를 발생시킨다.

DP(dynamic programming)
1. Overlapping Subproblem(겹치는 부분문제)
하나의 큰 문제가 여러 개의 부분문제로 쪼개질 수 있다. 이 부분문제들은 재사용되고 결과적으로 큰 문제의 해를 구하는데에 사용된다.
2. Optimal Substructure(최적 부분구조)
어떤 문제의 최적의 해가 부분 문제의 최적 해로부터 설계될 수 있다.
즉, 최적 부분구조일 때 문제의 해는 그 문제의 부분 문제의 해로부터 구할 수 있다.
n행 4열로 구성되어 있는 dp 테이블을 만들고, a행 b열에 a행 b열을 지나갈 경우의 최댓값을 저장한다.
n행까지의 최댓값은 결국 1~n-1행까지의 부분 최적해로 구할 수 있다.

(참고: https://velog.io/@polynomeer/%EB%8F%99%EC%A0%81-%EA%B3%84%ED%9A%8D%EB%B2%95Dynamic-Programming)

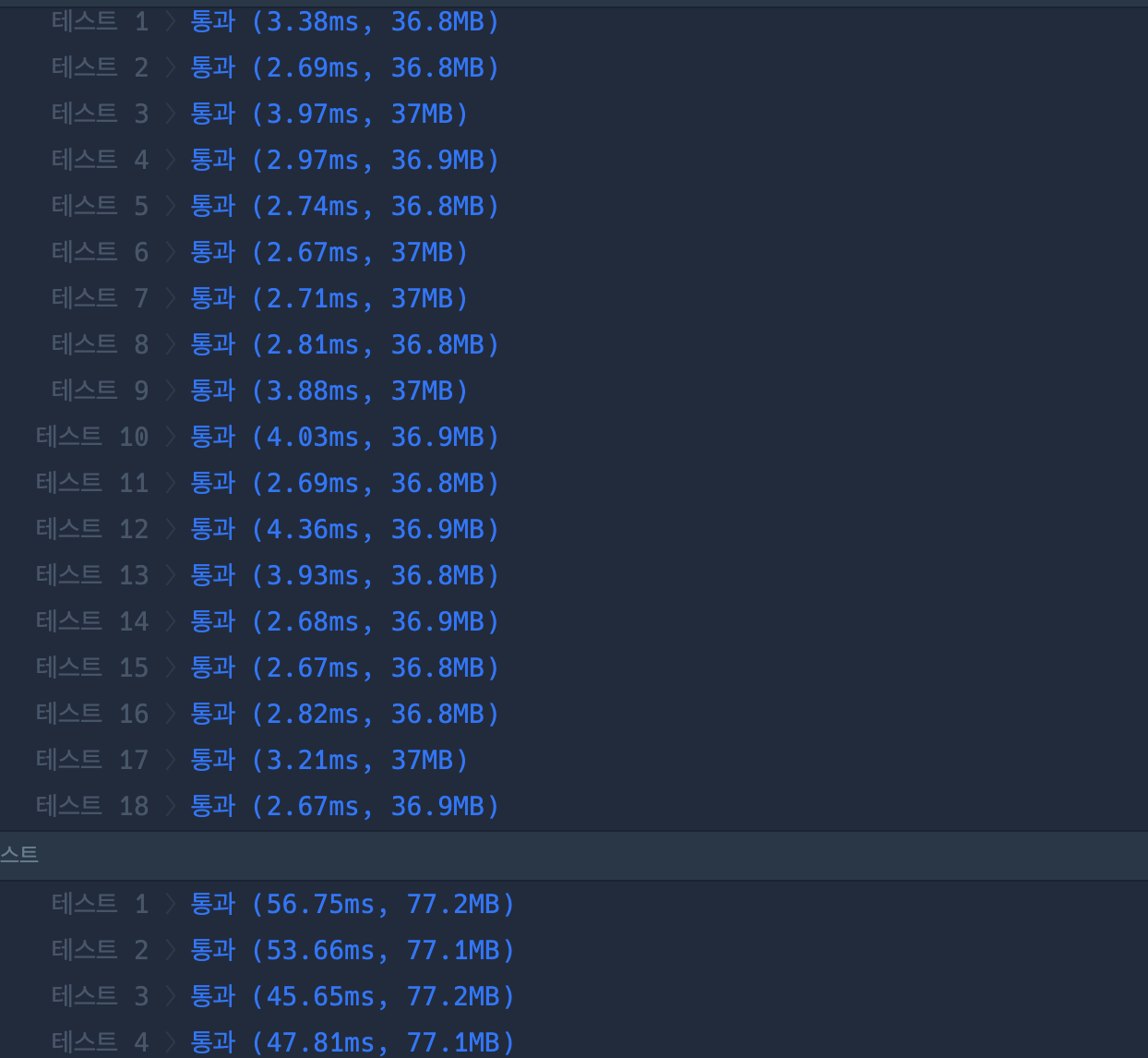
👆 1차 코드(전체 테스트케이스 시간초과)

function solution(land) {
    const N = land.length;
    let answer = 0;
    
    function dfs(curDepth, arr, temp){
        if (curDepth === N){
            if (temp > answer) answer = temp;
            return;
        }
        for (let i = 0; i < 4; i+=1){
            if (i !== arr[curDepth-1]) {
                dfs(curDepth+1,  arr.concat([i]), temp+land[curDepth][i]);
            }
        }
    }
    
    for (let i = 0; i < 4; i+=1){
         dfs(1, [i], land[0][i]);
    }
   
    return answer;
}

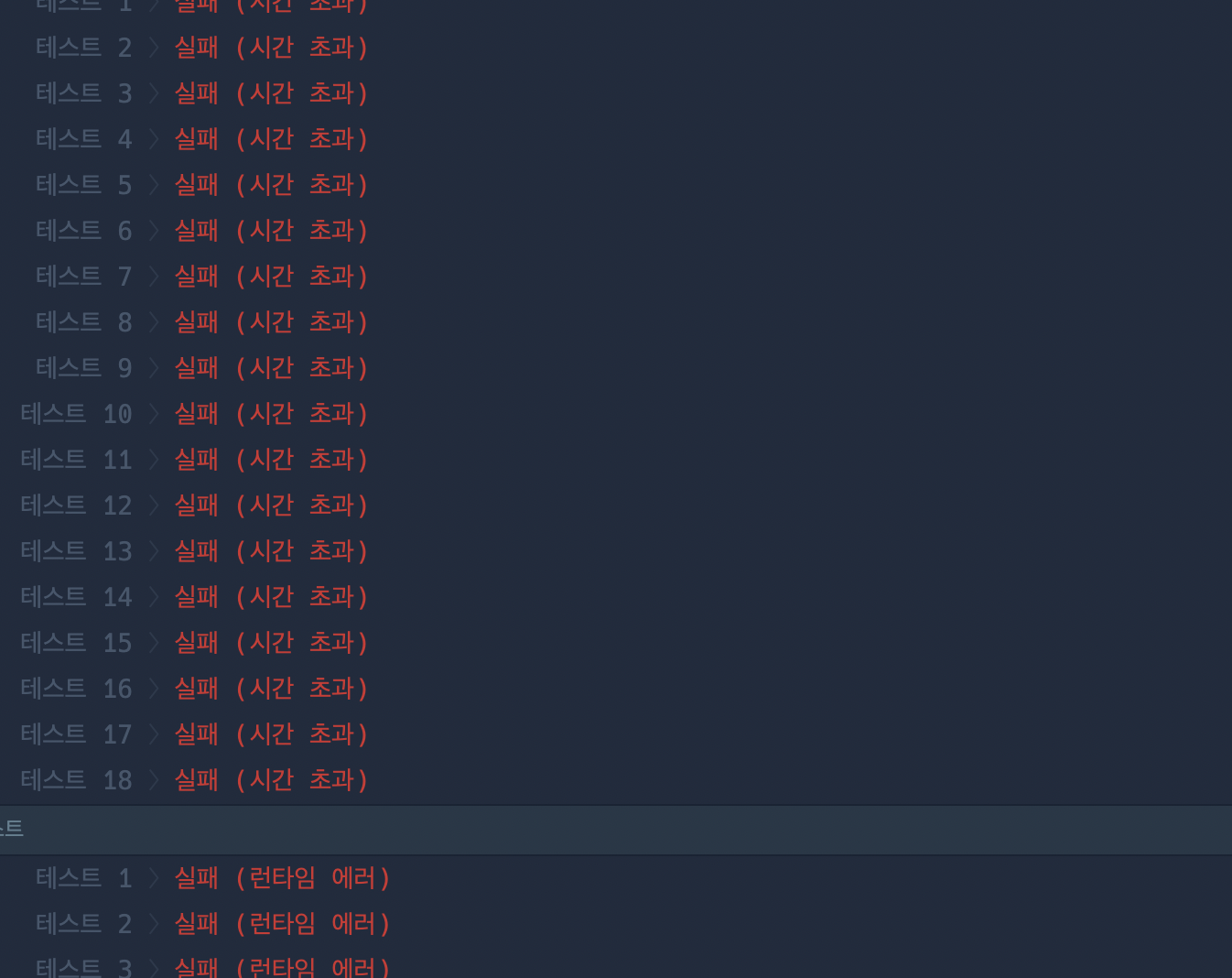
✌️ 2차 코드 (array.concat를 사용하지 않은 코드 - 그럼에도 시간초과)

function solution(land) {
    const N = land.length;
    let answer = 0;
    
    function dfs(curDepth, curCol, temp){
        if (curDepth === N){
            if (temp > answer) answer = temp;
            return;
        }
        for (let i = 0; i < 4; i+=1){
            if (i !== curCol) {
                dfs(curDepth+1,  i, temp+land[curDepth][i]);
            }
        }
    }
    
    for (let i = 0; i < 4; i+=1){
         dfs(1, i, land[0][i]);
    }
   
    return answer;
}

🤟 3차 코드 (다른 사람 풀이 참고)

function solution(land) {
    const N = land.length;
    for (let row = 1; row < N; row+=1){
        for (let col1 = 0 ; col1 < 4; col1+=1){
            let maxValue = 0;
            for (let col2 = 0; col2 < 4; col2 += 1){
                if (col2 !== col1){
                    if (maxValue < land[row-1][col2]) maxValue = land[row-1][col2];
                }
            }
            land[row][col1] += maxValue;
        }
    }
    return Math.max(...land[N-1])
}