
- 문제 ( 6236번 ) : 용돈 관리
- 며칠동안 용돈을 사용할건지 ( N ), 통장에서 인출을 몇번할건지에 ( M ) 대한 정보를 입력받으면 통장에서 돈을 한번 인출 시 얼마를 인출해야 정확하게 N일동안 M번 인출할 수 있는지 구하는 프로그램 작성.
- 현재 가지고 있는 금액으로 하루를 생활하지 못하면 남은 금액을 통장에 집어넣고 다시 인출해 사용.
- 정확히 M 번을 맞추기 위해 현재 가지고 있는 금액으로 하루를 생활할 수 있더라도 남은 금액을 통장에 넣고 다시 인출할 수 있다.
- 입력 및 출력
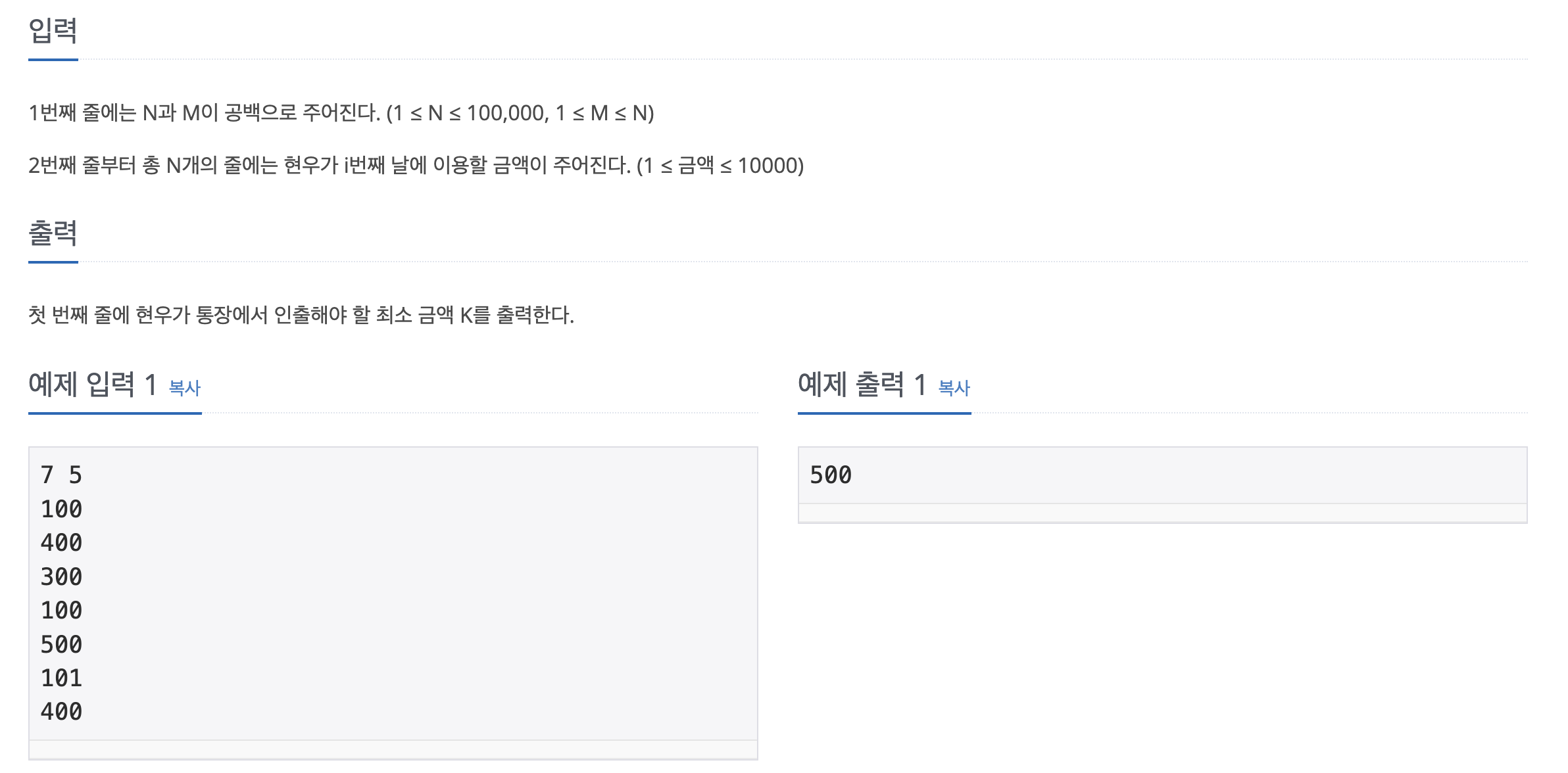
[ 입력 ]
- 첫번째 줄에 현우가 사용할 총 요일 ( N ) 과 인출 횟수 ( M ) 이 공백을 사이에 두고 입력.
( 1 ≤ N ≤ 100,000 , 1 ≤ M ≤ N )- 두번째 줄부터 총 N 개의 줄에 걸쳐 현우가 i 번째 날에 이용할 금액 입력.
( 1 ≤ 금액 ≤ 10,000 )
[ 출력 ]
- 첫 번째 줄에 현우가 통장에서 인출해야 할 최소금액 ( K ) 출력.
- 문제 풀이
-
이번 문제는 조건에 맞는 인출 금액 중 최소금액을 구하는 문제이다.
즉, 최소금액과 최대금액 사이에서 조건을 만족하는 금액을 찾아야 하는 문제이다.
naïve 하게 생각하면 최소금액인 1 부터 최대금액인 ( ∑ 입력받은 값 ) 까지 1씩 증가시켜가며 탐색하면 해결되는 문제지만, 시간초과가 발생하게 된다.따라서 이번 문제는 이진탐색 ( binary search ) 방법으로 해결하면 된다!
-
이진탐색 시 left, right 범위를 설정해줘야 한다.
이때 관심있는 mid 즉, 이진탐색을 통해 구해야하는 값은 한번 인출 시 뽑는 금액이다.
따라서 left 와 right 는 1원 ~ ( ∑ 입력받은 값 ) 이므로- left = 1
- right = ( ∑ 입력받은 값 )
으로 설정하면 된다.
그 후 이진탐색 방법대로 조건에 따라 left 를 mid+1 로 할지, right 를 mid-1 로 할지 결정해 값을 update 하며 최적의 값을 찾으면 해결된다! -
이진탐색을 하며 신경써야하는 부분은 다음과 같다.
- 오늘 써야하는 금액이 한번에 인출 가능한 금액보다 큰 경우
- 오늘 써야하는 금액이 내가 현재 가지고 있는 금액보다 큰 경우
- 내가 인출한 횟수가 주어진 인출 횟수 M 보다 큰 경우
이렇게 3가지의 경우를 고려해서 문제를 해결해야한다.
- 1, 3번의 경우 한번 인출 시 인출하는 금액을 늘리면 되므로 left = mid + 1 로 변경 후 계속해서 이진탐색 진행
- 2번의 경우 새롭게 인출하면 되므로 현재 가지고 있는 돈을 인출금액인 mid 로 update 하고 현재까지의 인출횟수를 1 증가시킨다.
-
이렇게 계속해서 이진탐색을 진행하면 문제가 해결되지만, 한가지 주의해야할 점이 있다.
이 전 이진탐색 문제에서는 조건에 맞는 mid 를 찾으면 그 값을 return 했지만, 여기서는 결괏값을 저장할 어떠한 변수에 중간에 저장해야한다.현재 해결한 코드에서는 right 의 값을 mid-1 로 update 하는 부분에서 result 라는 변수에 mid 를 저장해주었다.
이 말은 현재 mid 값이 현상황에서는 제일 작은 인출금액이라는 것이다.
그래서 result 라는 변수에 저장 후 이진탐색이 끝나면 이 result 값을 return 하면 된다.
-
k 를 구하는 함수를 따로 정의했으므로, 이 함수를 불러 얻어낸 return 값을 출력해주면 문제 해결!

- 최종 코드
- c++ code
#include <iostream>
using namespace std;
// N is day, M is # of withdraw
int N, M;
// list of money to spend
int money[100001] = {0, };
// get minimum K with binary search
int get_min_money(int total) {
int result = 0; // minimum K
int left = 1;
int right = total;
int mid = 0; // withdraw money
while(left <= right) {
mid = (left + right) / 2;
int current_money = mid;
int cnt = 1; // # of withdraw
bool pass = true; // today_money < withdraw money ?
for(int i = 0; i < N; i++) {
// if today_money > withdraw money? increase withdraw money
if(money[i] > mid) {
pass = false;
break;
}
// if today_money > current_money? withdraw money
if(money[i] > current_money) {
current_money = mid;
cnt++;
}
// spend money
current_money -= money[i];
}
// handle withdraw money
// case1. (today_money > withdraw money) or (# of withdraw > N)
// increase withdraw money and search again
if(!pass || cnt > M) {
left = mid + 1;
}
// case2. not case1
// decrease withdraw money and search again
else {
result = mid;
right = mid - 1;
}
}
return result;
}
int main() {
// input N and M
cin >> N >> M;
int total_money = 0;
// input money to spent
for(int i = 0; i < N; i++) {
cin >> money[i];
total_money += money[i];
}
// get minimum # of K
int K = get_min_money(total_money);
// print result K
cout << K << endl;
return 0;
}
- python code
# input n, m
# n is # of day, m is # of withdraw
n, m = map(int, input().split())
# list of money to spend
money = []
total = 0
for i in range(n):
a = int(input())
money.append(a)
total += a
# binary search
left = 1
right = total
min_k = 0 # minimum k
while (left <= right):
mid = (left + right) // 2
current_money = mid # available money
check = True # check ( today_money < current_money )
cnt = 1 # # of withdraw
for value in money:
# check1. is it possible? (today_money < current_money ?)
if(value > mid):
check = False
break
# check2. have enough money?
if(value > current_money):
current_money = mid
cnt += 1
current_money -= value
# update left and right
# case1. (today_money > withdraw_money) or (count > M) ?
if (not check) or (cnt > m):
left = mid+1
# otherwise
else:
min_k = mid
right = mid-1
# finish binary search ( = get minimum k )
print(min_k)