[C++] 백준 2178번 문제 풀이 ( 미로 탐색 )

- 문제 ( 2178번 ) : 미로 탐색

• 링크 : https://www.acmicpc.net/problem/2178

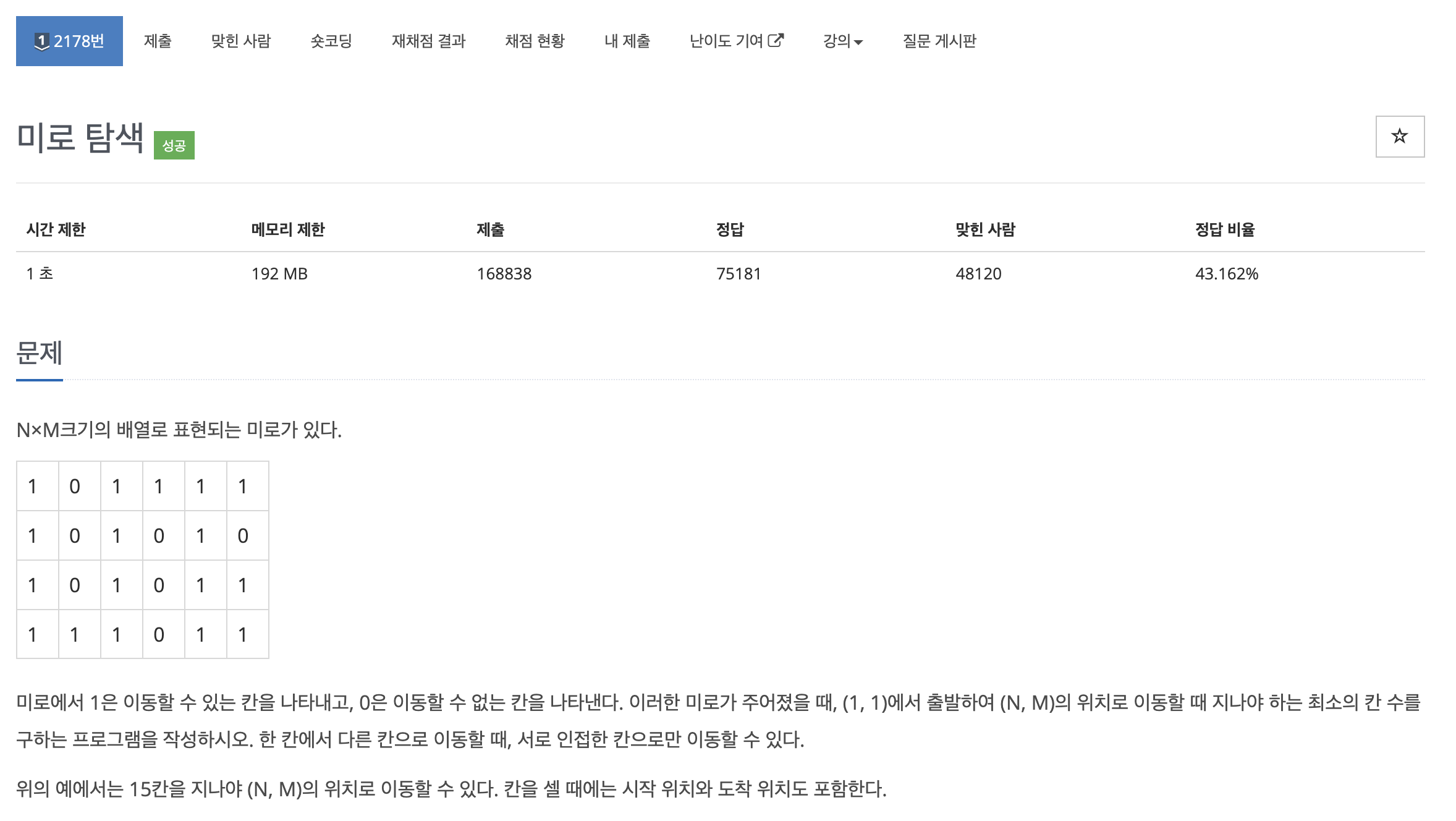
• 미로를 탈출할 때 지나는 칸의 최소 개수를 구하는 프로그램 작성.

  • 1은 지날 수 있는 칸, 0은 지날 수 없는 칸
  • 이동은 상, 하, 좌, 우 의 인접한 칸으로만 이동 가능.

---

- 입력 및 출력

[ 입력 ]

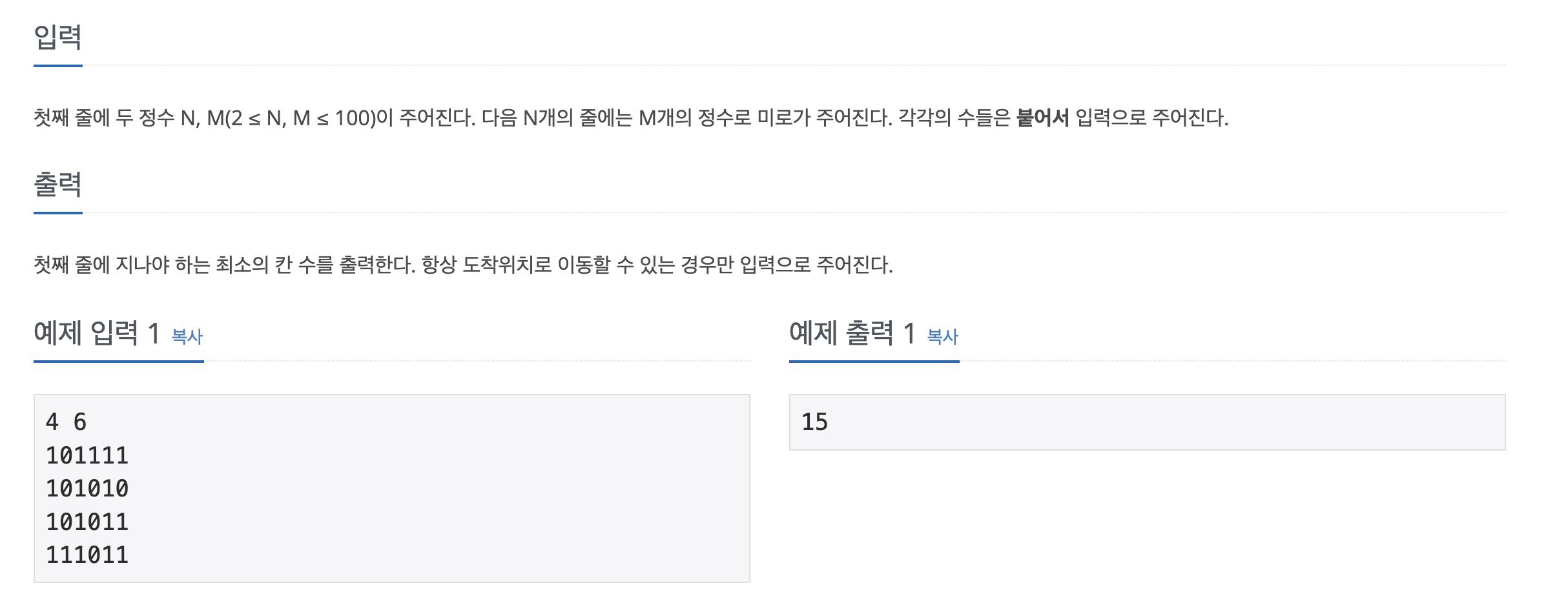
• 첫째 줄에 미로의 크기 N(가로), M(세로) 입력.
• 다음 N 개 줄에 M 개의 정수로 미로 입력.

  • 각각의 수들은 붙어서 입력.

• 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어짐.

[ 출력 ]

• 지나야 하는 최소의 칸 수 출력.

---

- 문제 풀이

• 이번 최단 칸수 구하기와 같은 유형의 문제는 그래프 탐색 방법중에서도 BFS 를 사용하면 쉽게 해결이 가능하다.

  BFS 는 현재 노드와 연결된 모든 노드 탐색 후 방금 탐색한 노드들을 기준으로 또 연결되어있는 모든 노드 탐색 . . . 해서 모든 노드를 전부 탐색하는 방법이다.

  이러한 유형의 문제를 BFS 로 풀면 하나의 노드마다 접근할 수 있는 곳을 알 수 있게 되고, 그 칸은 현재 노드 + 1 의 칸을 추가하면 접근할 때 거치는 최소 칸의 수를 저장할 수 있게 된다.

  이번 미로찾기 문제 역시 처음 시작지점부터 BFS 로 탐색을 시작한 후 마지막 최종 노드 위치에 저장된 방문한 칸의 개수를 출력하면 문제가 해결된다.

• 정리하면 아래와 같은 방식으로 해결할 수 있다.

1. 입력받은 시작점부터 BFS 탐색을 하는데, 현재 위치에서 상, 하, 좌, 우 를 탐색해 방문 가능하다면 현재 위치에 저장되어있는 방문 칸수 + 1 을 다음위치에 저장해준다.
2. 1번의 과정을 모든 노드에 대해서 반복한다. ( BFS 다보니 queue 에 push - pop 을 해주면서 queue 가 빌 때까지 반복 )
3. 최종적으로 도착위치 ( N, M ) 의 방문 칸수를 출력하면 해결!

• 문제를 풀면서 구현 상 신경써야 할 부분

  1. grid 의 입력이 공백 없이 붙어서 입력

     • 이 부분은

     scanf("%1d", &graph[i][j]);

     와 같이 입력받으면 해결

  
  2. 상, 하, 좌, 우 를 탐색하는 방법

  • 이 부분은 dx, dy technique 을 사용해 간단히 해결!

---

- 최종 코드

#include <iostream>
#include <queue>

#define N_MAX 100
#define M_MAX 100

using namespace std;

// 전역변수 설정
int N = 0, M = 0; // grid size (N x M)

// grid 선언
int graph[N_MAX][M_MAX] = {0, };

// 지나야 하는 최소의 칸 수 저장 배열
int result [N_MAX][M_MAX] = {0, };

// 상, 하, 좌, 우 를 탐색하기 위한 dx, dy 선언
int dx[4] = {-1, 1, 0, 0}; 
int dy[4] = {0, 0, -1, 1};

// 방문 확인 배열
bool is_visit[N_MAX][M_MAX] = {false, };

// 가능한 범위인지 확인
bool inRange(int x, int y) {
    // grid 를 벗어나지는 않았는지 확인
    bool ingrid = (0 <= x && x < N && 0 <= y && y < M);

    // 그 위치에 갈수없는 즉, 값이 0인지 확인
    bool possible_pos = (graph[x][y] != 0);

    return (ingrid && possible_pos);
}

// BFS 에서 사용할 queue
queue< pair <int, int> > q;


// BFS 탐색
void BFS(int x, int y) {

    // queue 가 빌 때까지 반복
    while(!q.empty()) {
        int a = q.front().first;
        int b = q.front().second;
        q.pop();

        // 현재 (a, b) 위치에서 상, 하, 좌, 우 4가지 방향 확인
        for(int i = 0; i < 4; i++) {

            // 다음 위치의 좌표 구하기
            int nx = a + dx[i];
            int ny = b + dy[i];

            // 가능한 범위라면 방문 확인 후 방문하지 않았다면 queue 에 위치 저장 후 
            // 이동할 때 지나야 하는 칸을 이전 방문 위치 (a, b) 의 값에 1 추가해 현재 좌표에 저장
            if(inRange(nx, ny) && (is_visit[nx][ny] == false)) {
                q.push(make_pair(nx, ny));
                is_visit[nx][ny] = true;
                result[nx][ny] = result[a][b] + 1;
            }

        }
    }
}

int main() {
    // grid size 입력
    cin >> N >> M;

    // grid 입력 (공백없이 붙어서 입력으로 주어지므로 정수 하나씩 받아서 처리)
    for(int i = 0; i < N; i++) {
        for(int j = 0; j < M; j++) {
            scanf("%1d", &graph[i][j]);
        }
    }

    // 첫번째 위치 queue 에 저장 후 방문 표시
    q.push(make_pair(0, 0));
    is_visit[0][0] = true;

    // 시작위치도 칸을 세므로 시작위치의 결과값 1 저장
    result[0][0] = 1;

    // BFS 로 방문하며 지나야 하는 최소의 칸수 구하기
    BFS(0, 0);

    // 도착 위치의 방문 칸 수 출력 (result)
    cout << result[N-1][M-1] << endl;

    return 0;
}