- 문제 (16974번) : 레벨 햄버거

- 햄버거의 레벨 N 을 입력받아 제공된 N-level 햄버거의 아래서부터 X 장을 먹었을 때 먹은 패티의 개수 구하기
- 0-level 햄버거 : p
- L-level 햄버거 : b ( l-1 level 햄버거 ) p ( l-1 level 햄버거 ) b
- p = 패티 || b = 햄버거번
- 입력 및 출력
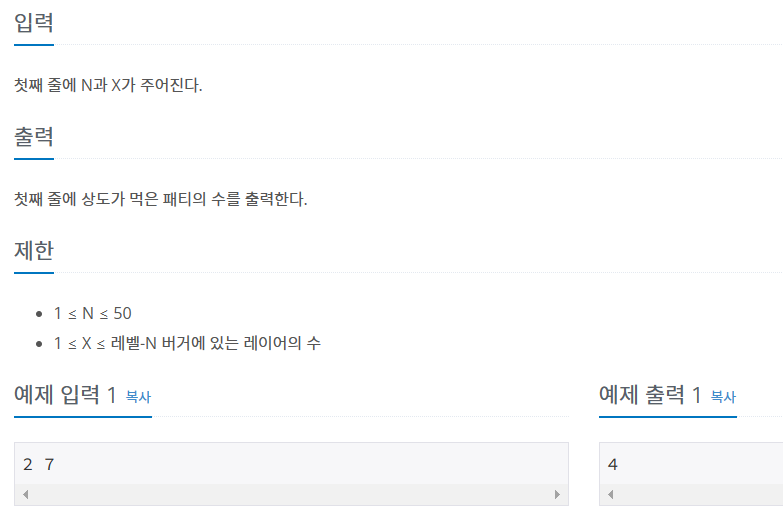
[ 입력 ]
- 첫째 줄에 햄버거 레벨 N 과 햄버거 바닥에서부터 먹은 X 층 입력
- 1 ≤ N ≤ 50 || 1 ≤ X ≤ N-level 버거에 있는 레이어의 수
[ 출력 ]
- 먹은 패티의 수 출력
- 문제 풀이
-
이 문제는 값이 비싼 재귀를 사용하는 것이므로 시간초과에 주의해 문제를 해결한다. ( 나도 시간초과로 많이 헤멤.. )
-
이 문제에서 입력으로 받을 수 있는 최대값은 50-level 햄버거의 레이어의 수가 될 것이다. ( 50보다 큼, long long 타입으로 처리해야 하는 사이즈 )
이렇게 크고 많은 햄버거를 전부 만들어서 하나하나 구하려고 하면 당연히 시간초과가 나게 될 것이다. ( 나는 처음에 이렇게 접근했음.. )
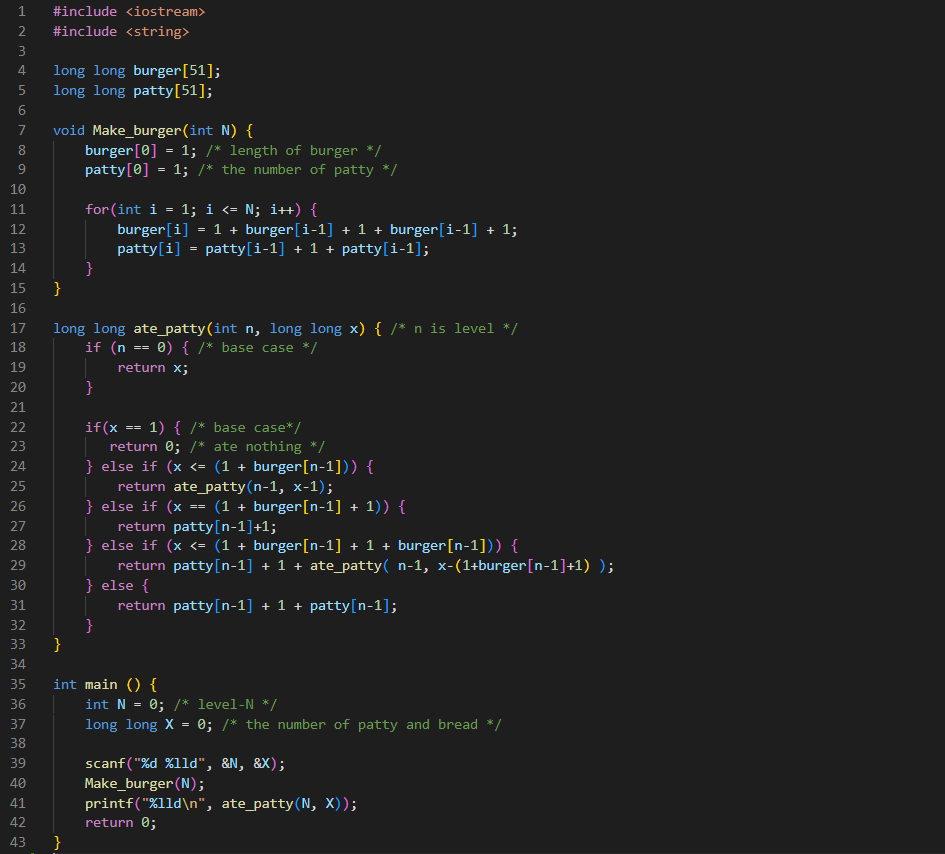
❗ 문제의 핵심은 dp의 memoization을 활용해 각 level 햄버거의 레이어수, 패티의 수를 기억한 후 각각의 상황에 맞춰 한번에 계산하는 것!
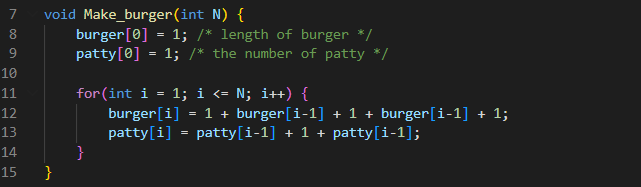
- memoization을 통한 값 계산
- 경우를 나눠 패티의 수 계산
- 나눌 수 있는 경우는 햄버거를 만드는 규칙에 주어져있다.
L-level 버거를 봤을 때 나눠지는 5가지 경우로 나누면 된다.
( 기준은 햄버거의 제일 아래부터 먹은 개수 X 가 기준이 됨. )
- X == 1인 경우, 즉 햄버거번만 먹은 경우
- X ≤ 햄버거번 + (L-1)-level 버거인 경우
- X == 햄버거번 + (L-1)-level 버거 + 패티인 경우
- X ≤ 햄버거번 + (L-1)-level 버거 + 패티 + (L-1)-level 버거인 경우
- 완성품을 다 먹는 경우
- 이렇게 경우의 수를 나눴다면 각각의 경우에 패티의 수를 구하는 수식을 작성해야 한다. 이때 재귀를 사용하면 쉽다.
- X == 1인 경우, 즉 햄버거번만 먹은 경우
- 햄버거번만 먹었으므로 0 return
- X ≤ 햄버거번 + (L-1)-level 버거인 경우
- L-level 버거가 만들어질 때 계속해서 앞에 햄버거번이 하나씩 붙게 된다. 따라서 level도 하나씩 줄이고 ( 햄버거번 제거 ), 제거한 햄버거번은 먹은 것이 되므로 X도 하나씩 줄여 재귀로 풀다보면 어느순간 base case에 도달해 값이 계산되게 된다.
- X == 햄버거번 + (L-1)-level 버거 + 패티인 경우
- dp로 구해놓은 L-1 level 버거의 패티개수 + 1 이 이 상황에서의 패티 개수이므로 이 값 return.
- X ≤ 햄버거번 + (L-1)-level 버거 + 패티 + (L-1)-level 버거인 경우
- 2번 상황처럼 재귀로 구한다.
4번 상황에서는 (L-1)-level 버거가 두개이다. 하지만 앞의 3번까지의 상황은 전부 먹으므로 3번 상황의 값 + 2번과 동일한 방법으로 도출해낸 값이 먹은 패티의 개수이므로 이 값 return.( 2번 상황과 다른점은 2번은 X에서 1을 제거했지만, 4번 상황은 처음에 [햄버거번 + (L-1)-level 버거 + 패티인 경우] 를 모두 제거해줘야 하므로 X - (1 + burger[l-1] + 1) 로 재귀를 돌려야 한다. )
- 완성품을 다 먹는 경우
- dp로 구해놓은 값들을 활용해 계산한 값 return.
( L-1 level 버거의 패티개수 + 1 + L-1 level 버거의 패티개수 )
- 이렇게 만든 함수들을 main 에서 호출해주면 문제 해결.
- 최종 코드