[C++] 백준 13023 번 풀이 ( ABCDE )

- 문제 ( 13023번 ) : ABCDE

• 링크 : https://www.acmicpc.net/problem/13023

• 사람의 수와 친구관계를 입력받았을 때 아래와 같은 친구관계를 가진 사람들이 존재하는지 확인하는 프로그램 작성.

  • A -> B -> C -> D -> E 의 관계
    
    
  • 이 관계에서 " -> " 는 친구라는 관계임.
  • 즉, A 는 B 와 친구이고 B 는 C 와 친구이고 . . . D 는 E 와 친구인 관계가 있는지 확인.

---

- 입력 및 출력

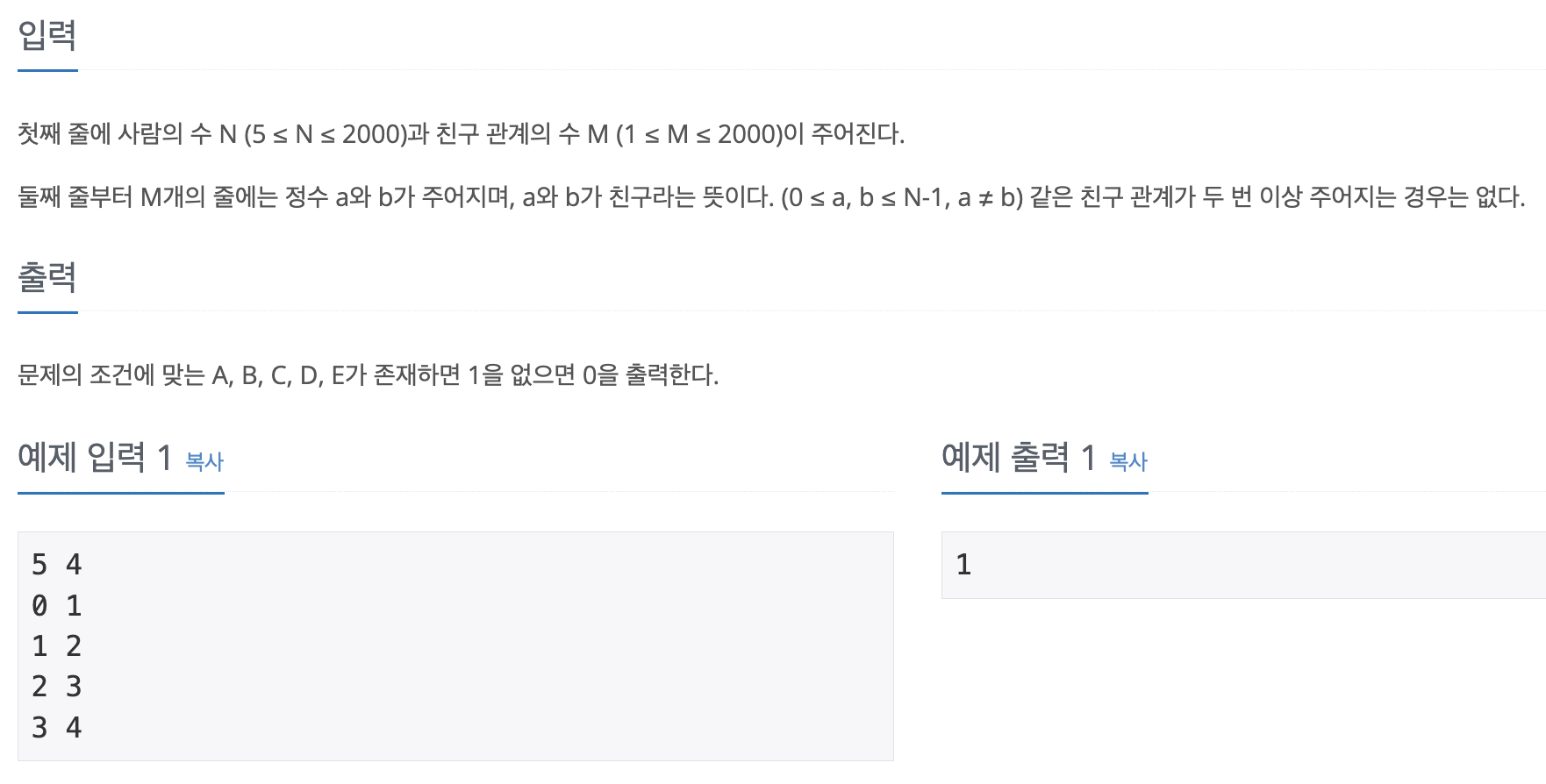
[ 입력 ]

• 첫째 줄에 사람의 수 ( 5 ≤ N ≤ 2,000 ) 와 친구 관계의 수 ( 1 ≤ M ≤ 2,000 ) 입력
• 둘째 줄부터 M 개의 줄에 걸쳐 친구관계의 수 주어짐.

  • 정수 a 와 b 가 주어지며, a 와 b 가 친구관계라는 의미.
  • a 와 b 는 0 ~ N-1 사이의 값.
  • 동일관계는 중복되어 주어지지 않음.

[ 출력 ]

• A -> B -> C -> D -> E 의 관계가 있다면 1을 그렇지 않다면 0을 출력

---

- 문제 풀이

• 이번 13023번 문제는 ( DFS 탐색 + back tracking ) 문제이다.

  백트래킹이란 해를 찾는 도중에 막히면 더 이상 깊이 들어가지 않고, 이전 단계로 되돌아가서 해를 찾아나가는 기법을 말한다. 최적화 문제와 결정 문제를 푸는 방법이 된다고 한다.

• back tracking 이란 경로를 따라가며 진행하다가 내가 구하고자하는 조건에 맞지 않으면 가지치기를 하는 방법이라고 할 수 있다.

  즉, back tracking 을 통해 불필요한 탐색을 진행하지 않아서 효율을 높일 수 있다.

• 이번 문제 역시 주어진 graph 를 깊이우선탐색 ( DFS ) 로 탐색하다가 조건을 만족하는 경우가 나타난다면 즉시 탐색을 종료하고 결과를 update 해서 답을 도출해내는 방식으로 해결하면 된다.

• 나는 문제를 이해하기 쉽도록 아래와 같이 말을 수정해보았다.

  • A -> B -> C -> D -> E 의 관계가 있다.
    -> 어떠한 node A 부터 DFS 탐색을 시작해 5번째 node 까지 도달하는 경우가 있다. ( = 탐색 깊이가 0에서 시작해 4까지 가는 경우가 있다.)
    
    
  • a 와 b 가 친구 관계이다.
    -> a 와 b 는 양방향 간선으로 연결되어있다. ( = a <-> b )

• 위와 같은 정보들을 가지고 아래의 방법으로 문제를 해결해나갔다.

  1. 친구관계를 graph 형태로 저장한다.
  2. N 명의 사람에 대해 DFS 탐색을 진행하며, 한명에 대해 DFS 탐색이 모두 끝난 후 결과 ( code 상에서 is_possible ) 를 확인해 true 라면 1 출력후 바로 프로그램 종료
  3. 우리가 중점적으로 봐야하는 정보는 DFS 탐색 시 깊이이므로 현재 node 와 함께 깊이정보를 인자로 전달해준다.
  4. is_possible 정보는 인자로 전달되는 깊이가 4일 경우 true 로 update 해주고, DFS 탐색은 is_possible 이 true 로 update 될 때 종료해준다.

• 여기서 주의할 점은, 한번 DFS 탐색 후 다시 돌아와서 탐색을 진행할 때 방문여부는 false 가 되어야한다. 그래야 다른 사람을 기준으로 DFS 탐색을 진행할 때 그 사람을 다시 방문할 수 있다.

• 위와 같은 방법으로 구현하면 문제 해결!

---

- 최종 코드

// A -> B -> C -> D -> E 를 만족하는 경우가 있는지 확인하는 문제
#include <iostream>
#include <vector>
#define N_MAX 2001
#define M_MAX 2001 // 관계의 최대 개수
using namespace std;

// 관계를 저장할 graph 선언 (인접리스트 형식)
vector<int> graph[M_MAX];

// 방문 여부 저장 배열
bool is_visit[N_MAX] = {false, };

// A -> B -> C -> D -> E 만족하는지 확인하는 변수
bool is_possible = false;

// args : node = 현재 node, cnt = DFS 가 불린 횟수 (깊이)
void DFS(int node, int cnt) {
    // DFS 가 5번 불렸다면 즉, 5명이 A -> B -> C -> D -> E 처럼 연결이 되어있다면 즉시 탐색 종료
    if(cnt == 4) {
        is_possible = true;
        return;
    }
    // 방문여부 update
    is_visit[node] = true;

    // 현재 node 에 연결되어있는 모든 node 에 대해서 방문여부 확인 후 false 라면 DFS 로 방문
    for(int i = 0; i < graph[node].size(); i++) {
        int next_node = graph[node][i];
        if(is_visit[next_node] == false) {
            DFS(next_node, cnt+1);

            // 현재 node 즉, code 상의 next_node 에 대해 DFS 로 방문한 뒤 다시 돌아왔다면
            // 다른 node 에 대해서 DFS 방문할 때 또 방문할 수 있어야 하므로 방문여부를 false 로 바꿔줌.
            // 즉, 이 문제는 back tracking 과 그래프탐색이 결합된 문제임.
            is_visit[next_node] = false;
        }
    }
}

int main() {
    // 사람의 수 N, 관계의 수 M 선언 및 입력
    int N = 0, M = 0;
    cin >> N >> M;

    // M 개의 관계 입력
    for(int i = 0; i < M; i++) {
        int a = 0, b = 0;
        cin >> a >> b;

        // a 와 b 가 친구라는 소리이니 graph 형태로 표현하면 양방향 그래프로 표현됨.
        graph[a].push_back(b);
        graph[b].push_back(a);
    }

    // graph 를 DFS 탐색하는데 A -> B -> C -> D -> E 를 만족한다는 것은 DFS 를 최소 5번 중첩된다는 의미
    // 즉 0번 ~ N-1번까지의 사람들을 DFS 로 방문
    for(int i = 0; i < N; i++) {
        // 한번도 관계를 본 적 없는 즉, 방문하지 않았던 사람이라면 DFS 방문
        if(is_visit[i] == false) {
            DFS(i, 0);
            is_visit[i] = false;
        }

        // DFS 로 탐색했을 때 A -> B -> C -> D -> E 가 만족한다면 1 출력 후 종료
        if(is_possible) {
            cout << 1 << "\n";
            return 0;
        }
    }

    // A -> B -> C -> D -> E 를 만족하지 못했다면 반복문을 끝낸후 이 부분을 실행
    // 즉, 0 출력 후 프로그램 종료
    cout << 0 << "\n";
    return 0; 
}