[C++] 백준 1260번 풀이 ( DFS 와 BFS )

- 문제 (1260번) : DFS 와 BFS

• 링크 : https://www.acmicpc.net/problem/1260

• 하나의 그래프를 입력받아 DFS 로 탐색한 결과와 BFS 로 탐색한 결과를 출력하는 프로그램 작성.

  • 방문할 수 있는 정점이 여러개인 경우, 정점번호가 작은 것을 먼저 방문.
  • 더 이상 방문할 수 있는 점이 없는 경우 종료.
  • 정점 번호는 1 ~ N 까지임.

---

- 입력 및 출력

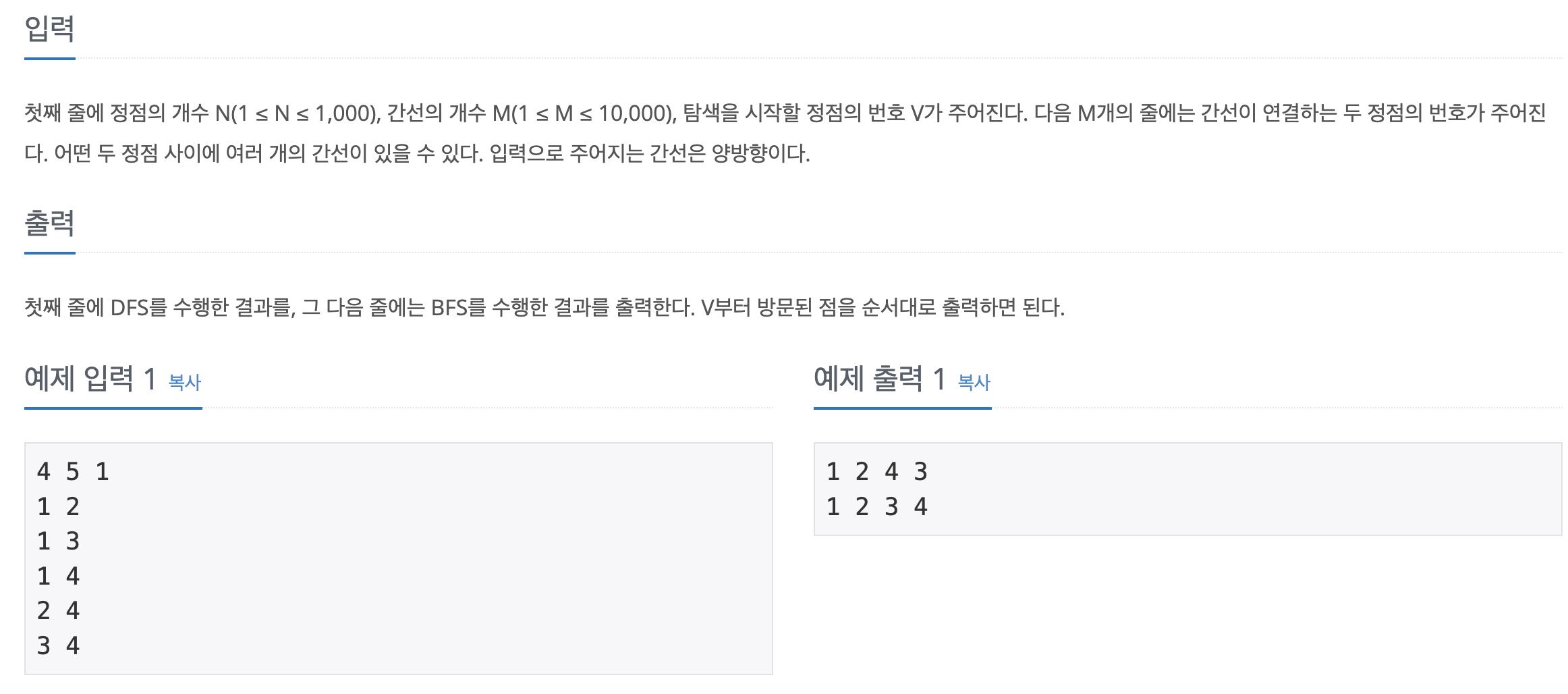
[ 입력 ]

• 첫째 줄에 정점의 개수 (N), 간선의 개수 (M), 탐색을 시작할 정점 (V) 입력.

  • 1 ≤ N ≤ 1,000
  • 1 ≤ M ≤ 10,000

• 다음 M 개의 줄에 걸쳐 하나의 간선이 연결하는 두 정점의 번호 입력.

• 어떤 두 정점 사이에 여러개의 간선 존재 가능.
• 입력으로 주어지는 간선은 양방향임.

[ 출력 ]

• 첫번째 줄에 graph 를 V부터 DFS 로 탐색한 결과 출력.
• 두번째 줄에 graph 를 V부터 BFS 로 탐색한 결과 출력.

---

- 문제 풀이

• 이번 문제는 그래프의 간선 ( edge ) 과 정점 ( vertax ) 을 입력받아 DFS 와 BFS 로의 탐색 결과를 출력하는 프로그램을 구현하는 문제이다.

  그렇다는 것은 DFS 와 BFS 가 무엇인지 알아야 해결할 수 있는 문제이다.

• DFS ( Depth-First Search ) : 깊이 우선 탐색

  • 정점에 연결되있는 노드를 하나씩 탐색하는 방법
  • 이름처럼 넓게 보는 것이 아닌 본인과 연결되어있는 노드 하나를 보고 그 하나와 연결되어있는 다른 정점부터 방문 후 다른 노드 방문하는 방법
  • 자료구조를 사용한다면 stack 을 사용해 풀이 가능.
  • 재귀를 사용하는 방법 역시 DFS 와 동일하게 탐색. ( 이 문제의 DFS 부분을 재귀로 탐색 )
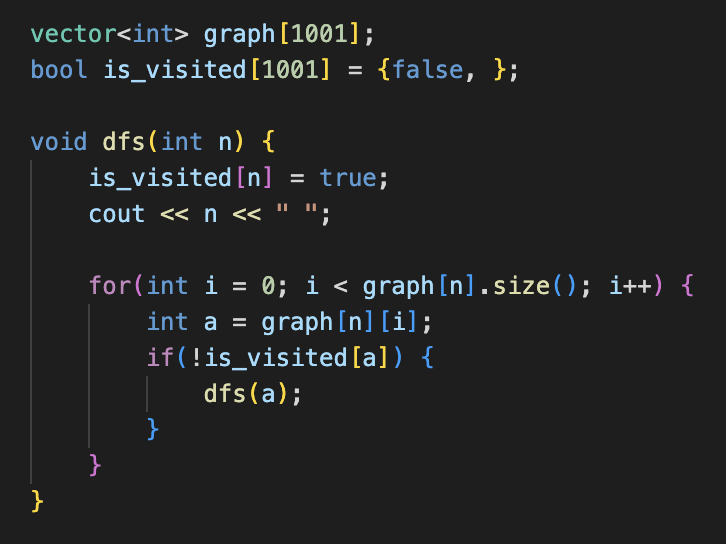
  • 재귀로 DFS 를 구현했을 때의 코드는 아래와 같다.
    

• BFS ( Breadth-First Search ) : 넓이 우선 탐색

  • 정점에 연결되어있는 모든 정점 방문 후 방문한 정점 중 하나에 연결되어있는 모든 정점 방문 . . . 의 과정을 그래프의 모든 정점에 대해 방문할 때까지 반복해 탐색하는 방법.
  • 이름처럼 넓게 탐색하는 방법
  • 자료구조 중 queue 를 사용하는 방법이 일반적임.
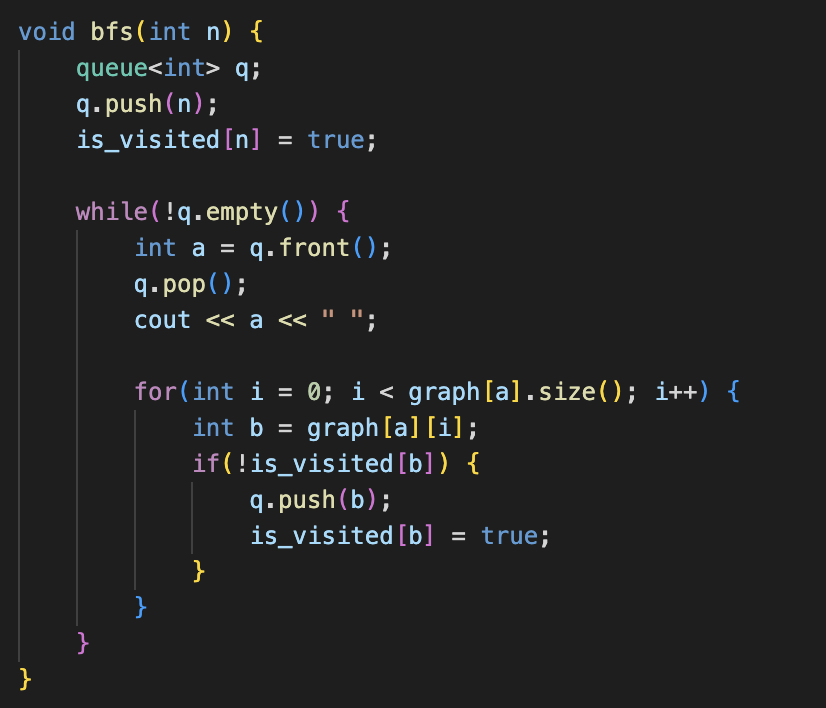
  • queue 를 사용해 BFS 를 구현한 코드는 아래와 같다.
    

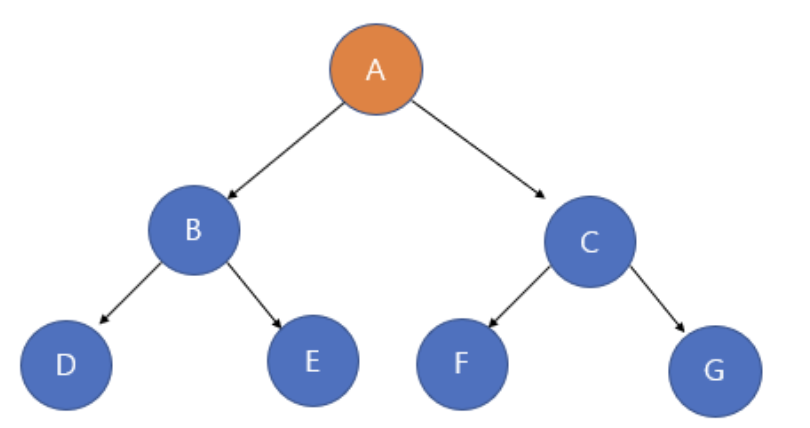
• 위와 같은 그래프가 있다면 DFS 와 BFS 의 결과는 아래와 같다.

  • DFS : A -> B -> D -> E -> C -> F -> G
  • BFS : A -> B -> C -> D -> E -> F -> G

• 그래서 위의 구현한 DFS, BFS 함수를 사용해 구현하면 문제 해결!

  1. 정점의 개수, 간선의 개수, 탐색 시작 노드를 입력받는다.
     
     
  2. 그 후 간선의 개수만큼 반복해서 정점 2개를 입력받는다.
     
     
  3. 프로그램에서 입력 받는 모든 간선은 양방향이라고 했으니 graph 에 양방향으로 edge 를 추가한다.
     
     
  4. 그 후 문제에서 " 방문할 수 있는 정점이 여러개인 경우, 정점번호가 작은 것을 먼저 방문 " 한다는 조건이 있으므로 graph 를 오름차순 정렬한다.
     
     
  5. 그 후 dfs 로 방문한다.
     
     
  6. dfs 로 방문했다면 방문했다고 표시하는 bool is_visited 배열의 값이 true 로 바뀌어있기 때문에 다시 false 로 초기화한다.
     
     
  7. 그 후 bfs 로 탐색을 진행한다.

• 위와 같이 main 함수를 구현하면 프로그램 해결!

---

- 최종 코드

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>

using namespace std;

vector<int> graph[1001];
bool is_visited[1001] = {false, };

void dfs(int n) {
    is_visited[n] = true;
    cout << n << " ";

    for(int i = 0; i < graph[n].size(); i++) {
        int a = graph[n][i];
        if(!is_visited[a]) {
            dfs(a);
        }
    }
}

void bfs(int n) {
    queue<int> q;
    q.push(n);
    is_visited[n] = true;

    while(!q.empty()) {
        int a = q.front();
        q.pop();
        cout << a << " ";

        for(int i = 0; i < graph[a].size(); i++) {
            int b = graph[a][i];
            if(!is_visited[b]) {
                q.push(b);
                is_visited[b] = true;
            }
        }
    }
}

int main() {
    
    // N is the number of vertax
    // M is the number of edge
    // V is start vertax
    int N, M, V = 0;
    cin >> N >> M >> V;

    for (int i = 0; i < M; i++) {
        int v1, v2 = 0; // edge v1 -> v2
        cin >> v1 >> v2;
        graph[v1].push_back(v2);
        graph[v2].push_back(v1);
    }

    for(int i = 0; i <= N; i++) {
        sort(graph[i].begin(), graph[i].end());
    }

    dfs(V);
    printf("\n");
    
    for(int i = 0; i < 1001; i++) {
        is_visited[i] = false;
    }

    bfs(V);
    printf("\n");
    return 0;
}