
출처
문제
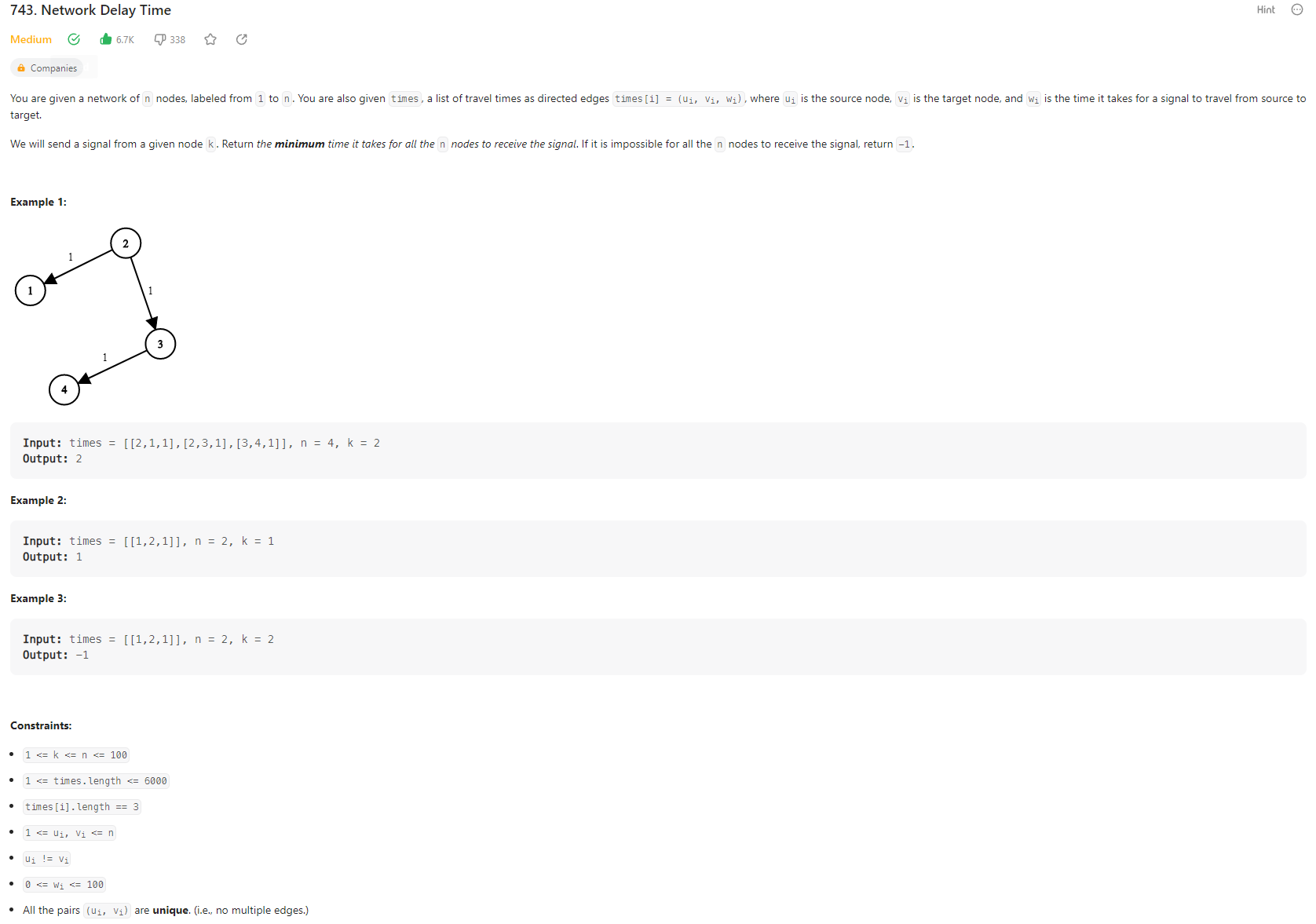
n개의 노드와 출발 노드 k, 노드의 연결 관계와 이동 시간을 나타내는 이차원 벡터가 주어졌을 때, 출발 노드로부터 모든 노드에 네트워크 신호를 전달하기까지 걸리는 최소 시간을 구하는 문제입니다.
특정 노드에서부터 다른 노드까지의 최단 거리를 구하는 다익스트라 알고리즘을 통해 문제를 해결하였습니다.
풀이
이 문제는 다익스트라 알고리즘만 제대로 구현할 수 있다면 쉽게 접근할 수 있는 문제입니다. 이 문제의 핵심 포인트는 다음과 같습니다.
- 노드 k에서 출발한 신호는 인접 노드에 동시에 퍼져나간다.
- 노드 k로부터 신호를 받지 못하는 노드가 있으면 -1을 반환한다.
먼저, 다익스트라 알고리즘을 통해서 시작 노드 k부터 다른 모든 노드까지 도달하는 데 걸리는 시간을 계산합니다. (우선순위 큐를 활용하면 시간복잡도를 최소화할 수 있습니다.) 다익스트라 알고리즘에서 기본적으로 거리 배열은 매우 큰 정수 (INF)로 초기화하기 때문에, 도달하지 못하는 노드가 있다면 해당 노드의 인덱스에 대한 거리 배열값은 갱신이 되지 않은 INF일 것이고, 이를 통해 거리 배열을 순회하면 신호가 도달하지 못하는 노드를 찾을 수 있습니다. 이 경우에 -1을 리턴하도록 하면 됩니다.
그리고 또 고려해야 할 점은 신호는 인접 노드에 동시다발적으로 퍼져나간다는 것인데, 이는 출발 노드와 가장 멀리 떨어진 노드에 신호가 도달했다면, 다른 모든 노드들에도 신호가 도달했다는 것을 의미합니다. 즉, 우리는 시작 노드 k에서부터 가장 멀리 있는 노드간의 거리만 파악한다면, 모든 노드에 신호가 전달되는 데 걸리는 최소 시간을 구할 수 있습니다.
코드는 아래와 같습니다.
#define pii pair<int, int>
class Solution {
public:
const int INF = 9999999;
const static int MAX_N = 101;
int dist[MAX_N]; // 출발 노드간의 최단 거리를 저장할 배열
vector<pii> graph[MAX_N];
void initDist() {
for (int i = 0; i < MAX_N; ++i) dist[i] = INF;
}
void dijkstra(int start) { // 출발 노드에서부터 모든 노드까지의 최단 거리 계산
priority_queue<pii, vector<pii>, greater<pii>> pq;
pq.emplace(0, start);
dist[start] = 0;
while (!pq.empty()) {
int cost = pq.top().first;
int cur = pq.top().second;
pq.pop();
if (dist[cur] < cost) continue; // 최단 거리가 구해진 경우 pass
for (int i = 0; i < graph[cur].size(); ++i) {
int next = graph[cur][i].first;
int newCost = cost + graph[cur][i].second;
if (dist[next] > newCost) {
dist[next] = newCost;
pq.emplace(newCost, next);
}
}
}
}
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
initDist();
for (int i = 0; i < times.size(); ++i) {
graph[times[i][0]].push_back({times[i][1], times[i][2]});
}
dijkstra(k);
int answer = 0;
for (int i = 1; i <= n; ++i) {
if (dist[i] == INF) return -1; // 도달하지 못하는 노드가 발견된 경우
answer = max(answer, dist[i]); // 가장 멀리 떨어진 노드 거리 갱신
}
return answer;
}
};시간복잡도
우선순위 큐를 활용한 다익스트라 알고리즘에서 노드 개수가 , 간선 개수가 일 때 의 시간복잡도를 보장하므로, 최종 시간복잡도는 입니다.
실행 결과

