Bayes Theory

베이즈 정리란 무엇인가요?

• 베이즈 정리는 확률론에서 조건부 확률을 계산하는 중요한 정리로, 새로운 정보를 바탕으로 어떤 사건의 확률을 업데이트하는 데 사용

수학적 표현

베이즈 정리는 다음과 같은 수식으로 표현됩니다:

여기서,

• ( P(A|B) ): 사건 B가 발생했을 때 사건 A가 발생할 조건부 확률 (사후 확률)
• ( P(B|A) ): 사건 A가 발생했을 때 사건 B가 발생할 조건부 확률 (가능도)
• ( P(A) ): 사건 A의 사전 확률
• ( P(B) ): 사건 B의 사전 확률

각 항목의 의미

• 사전 확률 ( P(A) ): 새로운 정보가 주어지기 전에 사건 A가 발생할 것으로 예상되는 확률입니다.
• 가능도 ( P(B|A) ): 사건 A가 발생한 조건에서 사건 B가 발생할 확률입니다.
• 사후 확률 ( P(A|B) ): 새로운 정보 B가 주어졌을 때 사건 A의 업데이트된 확률입니다.

예시로 이해하기

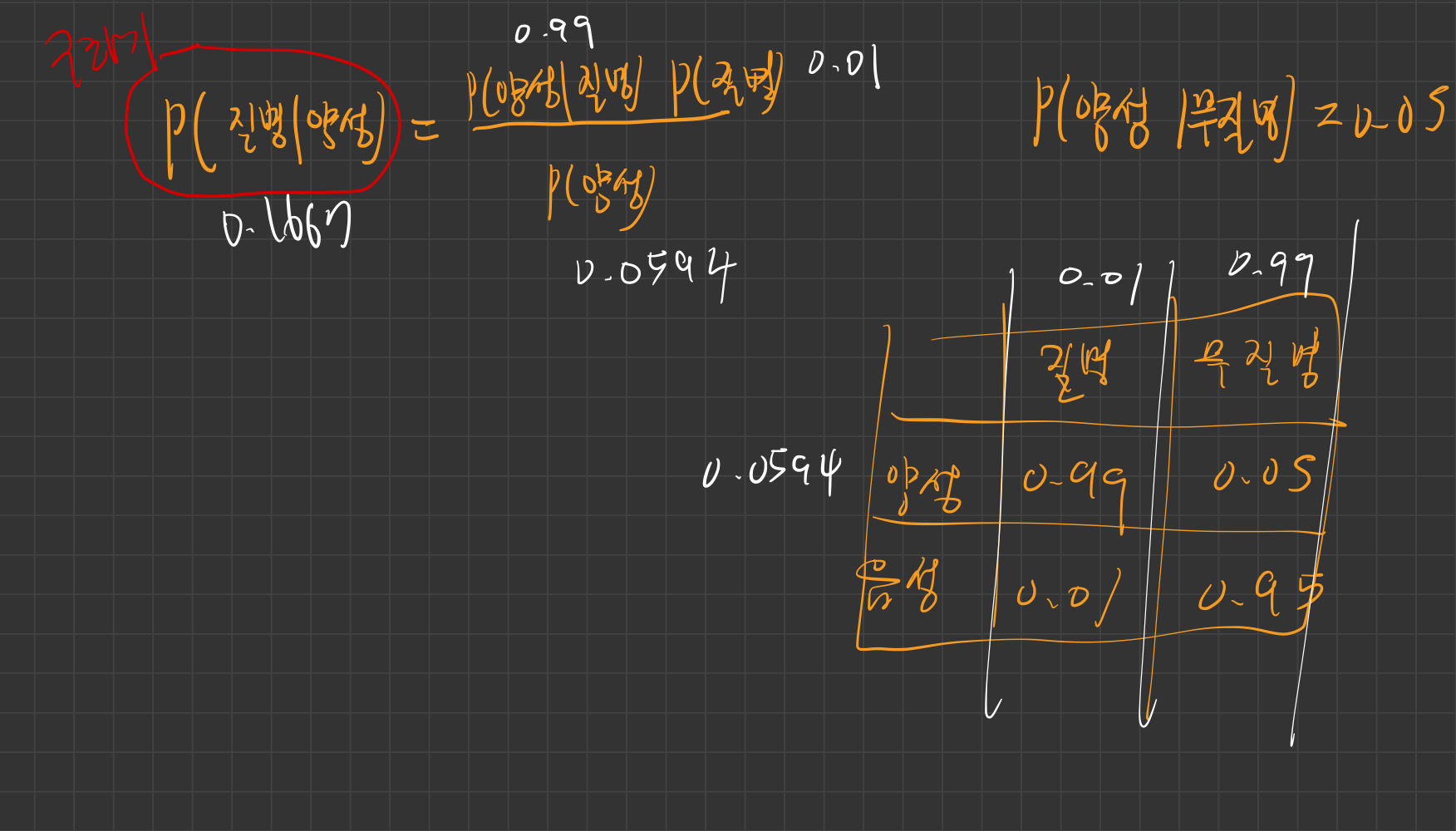
결과

검사 결과가 양성일 때 실제로 질병에 걸렸을 확률은 약 16.67%입니다.

해석

• 처음에는 검사에서 양성이 나오면 당연히 질병에 걸렸다고 생각할 수 있지만, 실제로는 그렇지 않습니다.
• 질병의 유병률이 낮고 검사에 거짓 양성이 존재하기 때문에, 양성 결과만으로는 확실하지 않습니다.
• 베이즈 정리를 사용함으로써 이러한 상황에서 실제 확률을 정확하게 계산할 수 있습니다.

결론

• 베이즈 정리는 새로운 정보를 고려하여 확률을 업데이트하는 강력한 도구입니다. 이를 통해 초기의 사전 확률을 새로운 증거와 결합하여 보다 정확한 사후 확률을 얻을 수 있습니다.