하노이탑

오늘은 하노이탑 알고리즘에 대해서 알아보는 시간을 가지겠다.

하노이탑은 어렸을 적 두뇌 발달용 장난감으로 많이 가지고 놀았었는데, 각설하고 바로 알고리즘부터 알아보도록 하겠다.
우선 하노이탑 알고리즘은 재귀함수로 작성된다.

n개의 원판을 옮기는 하노이탑의 기본 알고리즘은 이렇다. (위키백과 참조)

0. 원판이 1개일 경우 시작점에서 목적지로 바로 옮기면 된다.
1. n - 1 개의 원판을 가운데 기둥으로 옮긴다. (목적지가 경유지 역할)
2. 가장 큰 원판을 목적지로 옮긴다.
3. 경유지에 있는 n - 1 개의 원판을 목적지로 옮긴다.

이런식이다.

바로 Python 코드로 작성해보는 시간을 가지도록 하자

# n: 원판의 개수, start: 시작점, mid: 경유지, end: 목적지
def hanoi(n, start, mid, end):
	if n == 1: # 원판이 하나일 경우 바로 옮김
    	print(start, '->', end)
    	return 1
    # n-1개의 원판을 mid로 이동.(end가 경유지 역할)
    hanoi(n-1, start, end, mid)
    # 제일 큰 원판을 end로 옮김
    print(start, '->', end)
    # mid에 있는 n-1개의 원판을 end로 이동.(start가 경유지 역할)
    hanoi(n-1, mid, start, end)

이런식으로 작성이 가능하다. 실제로 동작 시켜 보면,
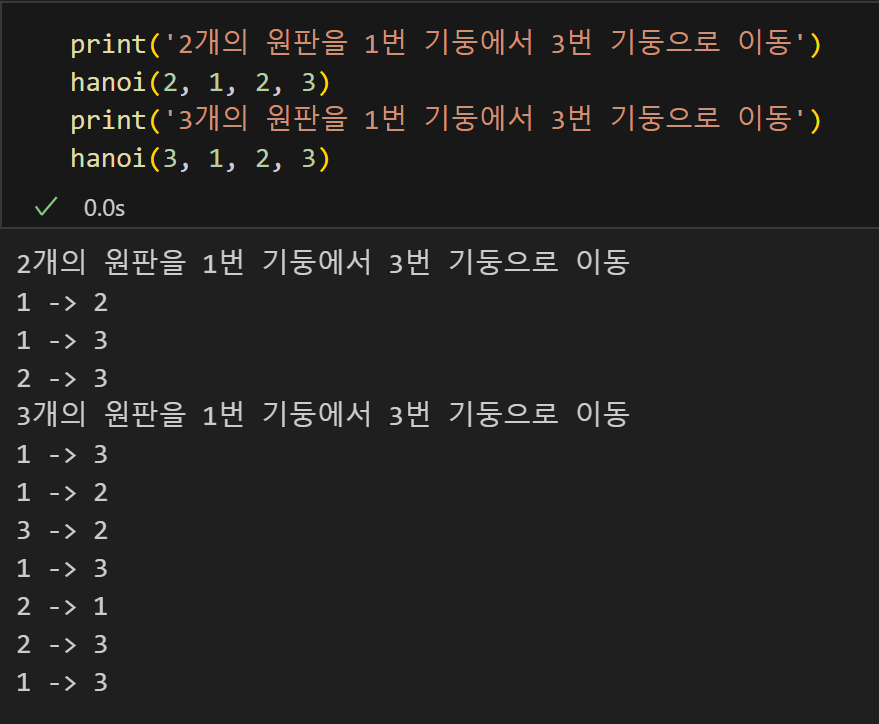이런식으로 아주 잘 동작하는 모습을 볼 수가 있다.

다른 코딩테스트 문제에서는 똑같은 알고리즘을 사용할 일이 없을 수도 있겠지만, 그래도 재귀함수에 대해서는 잘 이해할 수 있는 알고리즘인 것 같다.