RNN, BPTT 수식 유도

Recurrent Neural Networks

가변적인 길이의 시퀀스 데이터를 다룰 수 있는 신경망

• RNN은 시간 별로 같은 weight를 공유한다.
• 시퀀스 데이터: 소리, 문자열, ...

RNN을 도식화하면..

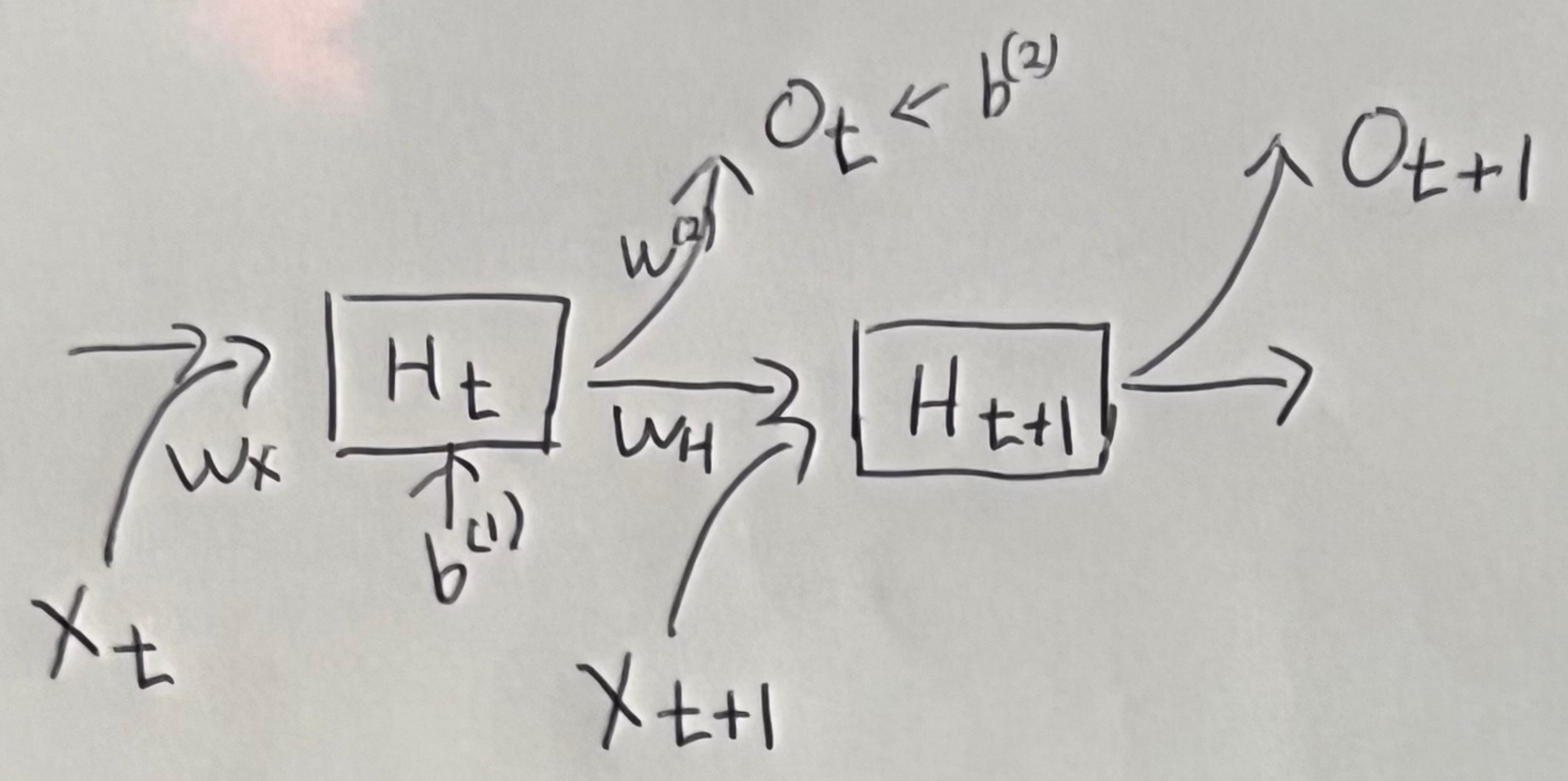
$\begin{aligned} & O_{t}=w^{(2)} H_{t}+b^{(2)} \\ & a_{t}=w_{x} X_{t}+w_{H} H_{t-1}+b^{(1)} \\ & H_{t}=\sigma\left(a_{t}\right) \end{aligned}$

• H: 잠재변수(상태변수), 시그마: 활성화함수, W: 가중치, b: 편향, t: 시간

BPTT

Back Propagation Through Time

• 각 time시리즈마다 존재하는 동일한 변수를 바꾼다.

수식 유도

• 목표 : Loss function을 출력과 잠재변수에 대해서 미분을 한 그래디언트를 구하는 것이 목표이다.
  $\begin{aligned} & L=\sum_{t} l_{t}: \text { 각각의 layer 에서의 loss의 합 } \end{aligned}$
  Loss function은 각각의 시간 t에 따른 layer에서의 loss의 합으로 표현할 수 있다.

  Loss function을 출력으로로 편미분한 그래디언트를 구해보면

  $\begin{aligned} & \frac{\partial L}{\partial O_{t}}=\frac{\partial\left(l_{t}+\cdots+l_{T}\right)}{\partial O_{t}}=\frac{\partial\left(l_{t}+\cdots+l_{T}\right)}{\partial l_{t}} \cdot \frac{\partial l_{t}}{\partial O_{t}} \\ & =\frac{\partial l_{t}}{\partial O_{t}} \end{aligned}$

  출력에 대한 그래디언트는 계산할 수 있다.
  (Loss function과 출력에도 활성화 함수가 존재하더라도 미분가능하다.)

Loss function을 상태변수로 편미분한 그래디언트를 구해보면

$\begin{aligned} & \frac{\partial L}{\partial H_{t}}=\frac{\partial l_{t}}{\partial H_{t}}+\frac{\partial l_{t+1}}{\partial H_{t}}+\cdots+\frac{\partial l_{T}}{\partial H_{t}} \\ & =\frac{\partial l_{t}}{\partial O_{t}} \cdot \frac{\partial O_{t}}{\partial H_{t}}+\cdots+\frac{\partial l_{T}}{\partial H_{t}} \end{aligned}$

$\begin{aligned} & =L^{\prime} w^{(2)}+\frac{\partial L_{t+1}}{\partial O_{t+1}} \cdot \frac{\partial O_{t+1}}{\partial H_{t+1}} \cdot \frac{\partial H_{t+1}}{\partial H_{t}} \end{aligned}$

$\begin{aligned} [\frac{\partial l_{t+1}}{\partial H_{t}}+\cdots+\frac{\partial l_{T}}{\partial H_{t}} = \frac{\partial L_{t+1}}{\partial H_{t}}, \text {네모 박스}=\frac{\partial L_{t+1}}{\partial H_{t+1}}]\end{aligned}$

$\begin{aligned} & \delta=L^{\prime} w^{(2)}+\delta^{+} \frac{\partial H_{t+1}}{\partial H_{t}} \end{aligned}$

각각의 W, b에 대한 그래디언트 값은 활성화함수가 정해지면 연쇄법칙을 사용하여 구할 수 있고 이를 이용해서 BPTT를 수행할 수 있게 된다.

• 수식을 자세히보면 BPTT를 수행시에 t+1번째 부터 앞으로 그래디언트 값이 전달되면서 미분의 곱으로 이루어진 항이 존재하게 되는 것을 볼 수 있다.
  e.g.나는 밥을 먹는다. 등의 시퀀스 데이터를 학습할 때 나라는 주어가 BPTT수행시에 사라질 수 있는데 이를 해결하기 위해 LSTM이나 GRU같은 모델을 사용하게 된다.

참고자료

• https://www.youtube.com/watch?v=4jgHzgxBnGY

유용한 도구

• 수기로 작성한 수식을 촬영 후에 PDF파일로 만들면 자동으로 latex형태로 변환해준다. 앞으로 종종 활용해보아야겠다.
  https://mathpix.com/image-to-latex
  내 글씨를 알아보다니.. 신기하다