*참고 : 저서 '이것이 코딩 테스트다 with Python', 코드트리 문제 오답리뷰
코테 준비 중에 가장 약하다고 생각하는 그래프 문제를 풀던 중에 '위상정렬'이라는 개념을 접하게 되었습니다. 이름은 많이 들어봤으나 제대로 정리해본 적이 없어서 위상정렬 문제도 못풀게 되었는데요, 이번에 오답문제를 다시 풀어보기 전에 제대로 공부해보도록 하겠습니다. 🧐
위상정렬 알고리즘이란?
위상정렬은 사이클리 없는 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것을 의미합니다.
개념만 보아서는 이해가 외지 않지 않죠? 예시를 들어보겠습니다.
대학교 강의 수업 중 자료구조, 알고리즘, 고급알고리즘이 있다고 합시다.
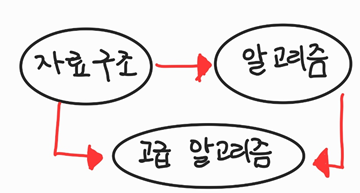
선수과목을 방향성을 고려해서 그래프를 그려보면 이렇게 된다고 가정합니다.
그렇다면 세 과목을 모두 수강하기 위한 적절한 학습 순서는 무엇일까요?
1) 자료구조 --> 고급 알고리즘 --> 알고리즘
2) 자료구조 --> 알고리즘 --> 고급 알고리즘
위 두 가지 방법 중 1번은 적절치 않습니다. 고급 알고리즘 수업을 듣고 알고리즘 수업을 들을 수는 없기 때문입니다.
개념을 알았으니, 이 외에도 꼭 알아둬야 할 용어가 있습니다.
진입차수 (Indegree)와 진출차수(Outdegree)입니다. 용어보다 뜻은 훨씬 쉽습니다!
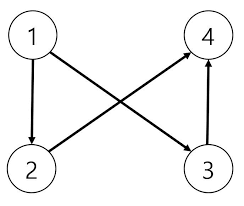
- 진입차수 : 특정한 노드로 들어오는 간선의 개수
- 진출차수 : 특정한 노드에서 나가는 간선의 개수
따라서 위 이미지에서 1번 노드는 진입차수는 0개, 진출차수는 2개입니다. 2번노드에는 진입차수는 1개, 진출차수는 1개입니다.
이제 필요한 개념은 모두 알아보았습니다. 그렇다면 파이썬 기준에서 위상정렬을 구현하기 위한 자료구조와 구현 과정을 알아보겠습니다.
🏠 구현 방식
파이썬에서는 Deque(큐)를 이용합니다.
구현순서는 다음과 같습니다.
1) 진입차수가 0인 모든 노드를 큐에 넣습니다.
2) 큐가 빌 때까지 다음의 과정을 반복합니다.
2-1) 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거합니다.
2-2) 새롭게 진입차수가 0이 된 노드를 큐에 넣습니다.
3) 각 노드가 큐에 들어온 순서는 위상정렬 알고리즘을 수행한 결과와 같습니다.
예시를 들어보겠습니다.
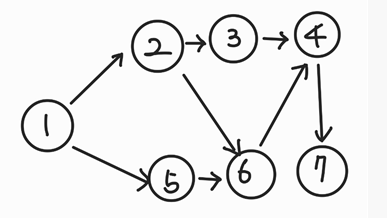
위 그림에서 진입차수가 0인 노드는 1번노드입니다.
1번 노드를 큐에 넣습니다.
큐에서 노드 1을 꺼낸 뒤 노드 1에서 나가는 간선을 제거합니다. (2번, 5번 노드로 가는 간선이 제거됩니다.)
진입차수가 0이된 노드는 노드2, 노드5가 됩니다.
큐에 노드2, 노드5를 넣습니다.
큐에서 노드2를 꺼낸 뒤 노드3, 노드6으로 나가는 간선을 제거합니다.
진입차수가 0인 된 노드는 3번이 됩니다.
큐에 노드3을 넣습니다.
.
.
.
위와 같은 과정을 반복하면 큐에 들어간 노드의 순서, 즉 위상정렬 알고리즘을 수행한 순서는
1 -> 2 -> 5 -> 3 -> 6 -> 4 -> 7
입니다.
✅ 이때 큐에 새롭게 들어가는 원소가 2개 이상일 경우 여러가지 답이 나올 수도 있습니다.
📜구현 코드
파이썬으로 다음의 과정을 구현한 코드를 살펴봅시다. 코드를 보면 시간복잡도는 O(V+E)이 됩니다.
from collections import deque
# 노드의 개수 : v, 간선의 개수 : e
v, e = map(int, input().split())
# 모든 노드의 진입차수는 0으로 초기화
indegree = [0]*(v+1)
# 각 노드에 연결된 간선 정보 리스트
graph = [[] for i in range(v+1)]
for _ in range(e):
a, b = map(int, input().split())
graph[a].append(b)
indegree[b] += 1
# 위상정렬 알고리즘 함수
def topology_sort():
result = []
que = deque()
# 진입차수가 0인 노드를 큐에 삽입
for i in range(1, v+1):
if indegree[i] == 0:
que.append(i)
while que:
now = que.popleft()
# 큐에 들어갔던 순서대로 결과리스트에 추가
result.append(now)
for i in graph[now]:
# 진입 간선 삭제
indegree[i] -= 1
# 진입차수가 0이 된다면 새롭게 큐에 삽입
if indegree[i] == 0:
que.append(i)
print(*result)
topology_sort()
# 결과값 : 1 2 5 3 6 4 7♻️ 실제 문제로 응용하기
기본적인 구현만 끝내고 가면 아쉬우니, 포스팅의 이유기도 했던 오답 문제를 다시 뜯어보겠습니다.
문제 >
크기가 N인 수열이 있고, 1번부터 N번까지의 번호를 갖고 있습니다.
첫 번째 줄에 정수의 개수 N과 두 수를 비교한 횟수인 M이 공백을 사이에 두고 주어집니다.특정 두 수의 크기를 비교한 정보가 입력으로 M개 주어집니다. 예를 들어, a, b 쌍이 입력되었다면, a번 정수가 b번 정수보다 작다는 것을 의미합니다.
수열을 오름차순으로 나열 했을 때의 번호 순서를 출력하는 프로그램을 작성해보세요. 이 때 답이 여러개라면 사전 순으로 가장 앞선 답을 출력하세요.
- 조건 : 1≤N,M≤100,000
딱 보면 위상정렬이라고 알아차리기 쉽지 않습니다. O(NlogN)을 보장하는 퀵 정렬을 해도 시간복잡도면에서 해결가능합니다. 하지만 이왕 위상정렬 알고리즘을 공부했으니 위상정렬 알고리즘으로 해결하겠습니다.
해결방법은 다음과 같습니다. deque대신 heap을 사용해서 구현하는 것입니다. 가장 작은 노드를 먼저 골라주는 우선순위 큐를 이용해야 하기 때문입니다.
코드로 구현해보도록 하겠습니다.
import heapq
n, m = map(int, input().split())
graph = [[] for _ in range(n+1)]
indegree = [0]*(n+1)
for _ in range(m):
a, b = map(int, input().split())
indegree[b] += 1
graph[a].append(b)
def topology_sort():
result = []
que = []
for e in range(1, n+1):
if indegree[e] == 0:
heapq.heappush(que, e)
while que:
now = heapq.heappop(que)
result.append(now)
for i in graph[now]:
indegree[i] -= 1
if indegree[i] == 0:
heapq.heappush(que, i)
print(*result)
topology_sort()
위에서 기본적인 알고리즘 구현코드와 굉장히 유사합니다! 여러 문제를 접해보면서 위상정렬인지를 알아보는 능력을 키운다면 앞으로 문제없이 해결가능할 것 같습니다. 😎
