Day 1
Simple Regression
warm up
데이터 예측 방법
- 기존 경험을 바탕으로 예측
- 통계 정보 활용 (ex. MAE)
- 예측 모델 활용 (ex. scatter plot에 가장 잘 맞는 직선, 회귀선:RSS 최소화 직선)
Baseline Model (기준모델) : 최소한의 성능을 나타내는 기준 모델
- 분류문제 : 타겟의 최빈값
- 회귀문제 : 타겟의 평균값
- 시계열 회귀문제 : 이전 타임스탬프 값
종속변수 = 반응변수 = 레이블 = 타겟
독립변수 = 예측변수 = 설명변수 = 특성(feature)
찾고자 하는 값이 어디에 있을까?
- 보간 : 기존 데이터 범위 내에서 값을 찾을 때
- 외삽 : 기존 범위를 벗어난 값을 찾을 때
- 선형회귀로 외삽할 때의 문제점 : 선형이 비선형으로 바뀔 가능성 有, 정확도의 감소(-> error증가), 엄청 작은 값으로 외삽했을 때 음수값 도출(-> 집값 등을 예측하는 경우라면 비상식적인 예측값)
- 보간과 외삽은 모델을 표현하는 선(회귀선)에 올라가 있는 값으로 표현됨
skikit-learn을 통한 선형회귀모델 만들기
- data 준비 ->
fit()메소드 사용해 모델 학습 ->predict()메소드로 예측
- 데이터 구조
- feature matrix : X, 2차원 행렬, 주로 numpy 행렬 or pandas 데이터프레임
- labels matrix : y, 1차원 행렬, 주로 numpy 배열 or pandas series
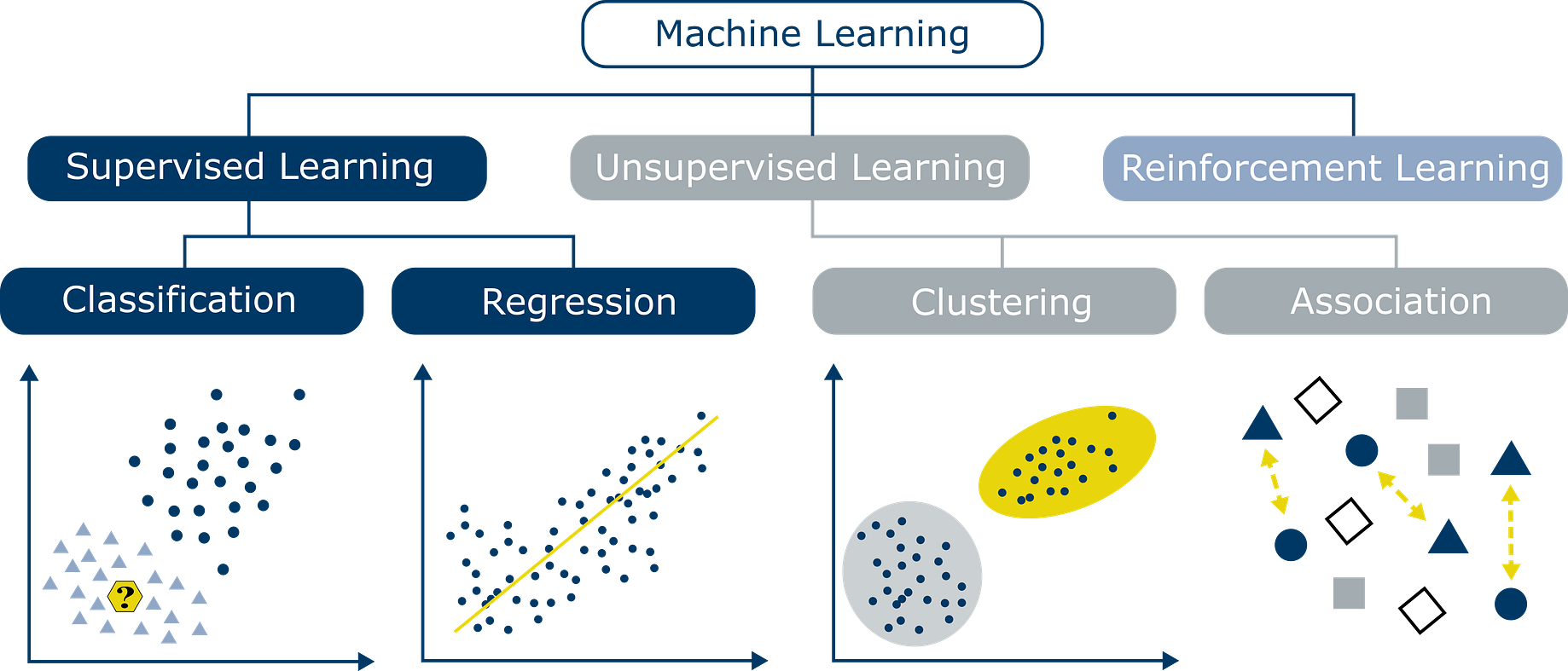
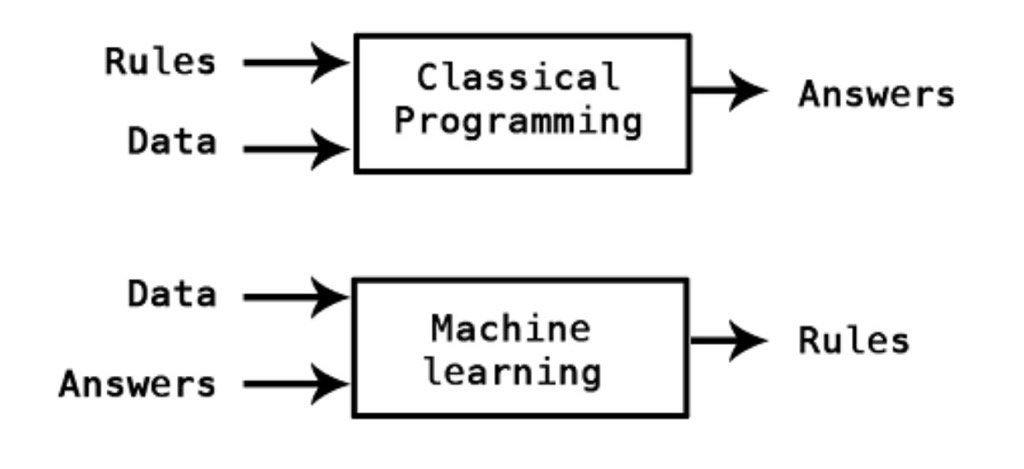
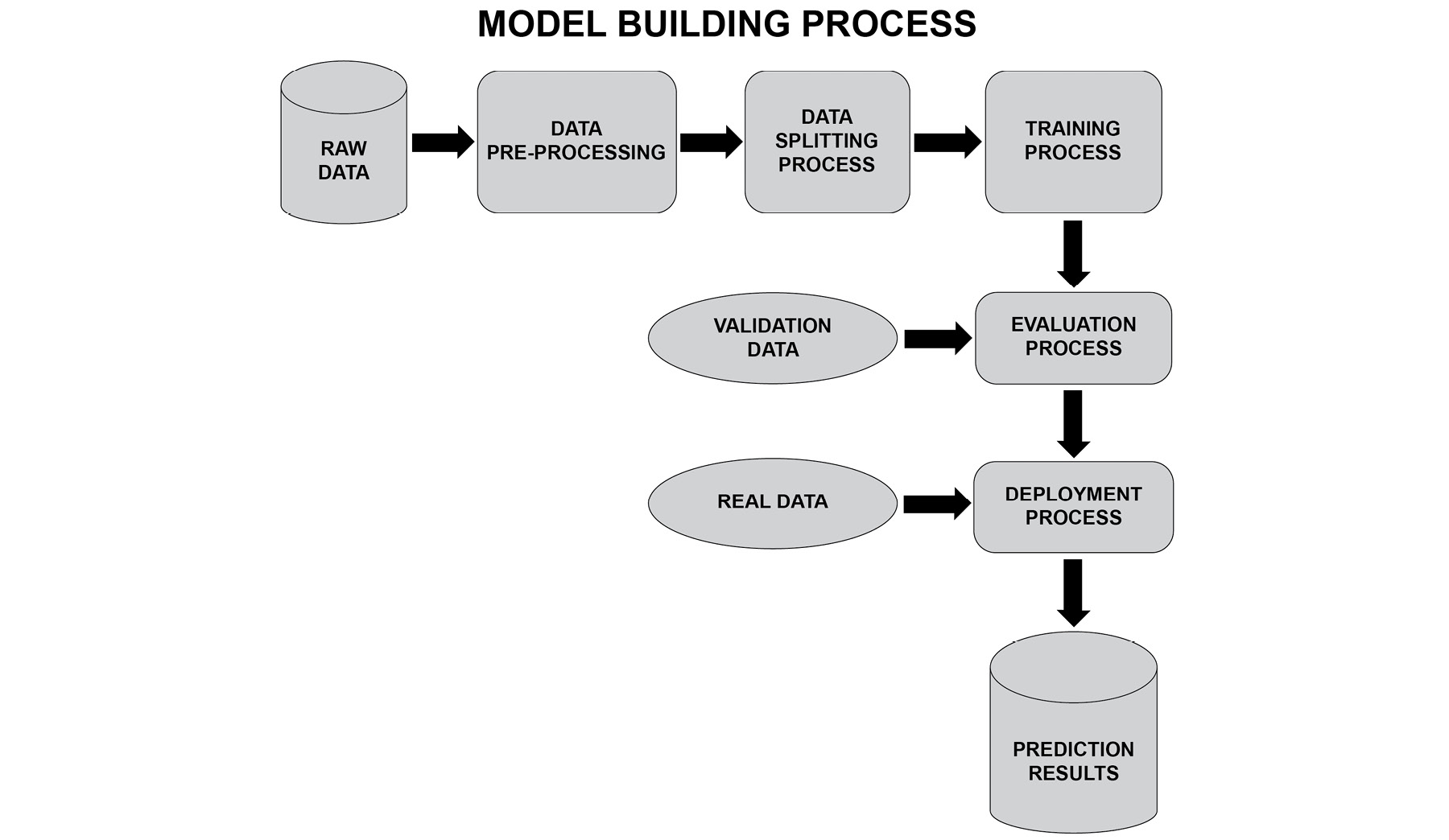
머신러닝 프로세스
선형회귀 가정
- X,y 사이의 선형성
- 잔차의 독립성
- 등분산성
- 정규성
상관관계와 선형회귀
설득력
상관관계가 없어도 선형회귀선을 그릴 수 있지만, 상관관계가 낮으면 선형회귀선의 설득력이 낮아져 필요 없어짐
Day 2
Multiple Regression
train/test set 나누는 이유
- 새로운 데이터에서도 적용(예측)가능한지가 목적
- 만든 모델의 예측 성능 제대로 평가 가능
회귀모델을 평가하는 지표들
- MSE (Mean Squared Error) =
- MAE (Mean absolute error) =
- RMSE (Root Mean Squared Error) =
- R-squared (Coefficient of determination) =
- 참고
- SSE(Sum of Squares
Error, 관측치와 예측치 차이): - SSR(Sum of Squares due to
Regression, 예측치와 평균 차이): - SST(Sum of Squares
Total, 관측치와 평균 차이): , SSE + SSR
- SSE(Sum of Squares
과적합과 과소적합
일반화(generalization)
- 테스트데이터에서 만들어 내는 오차 : 일반화 오차
- 훈련데이터에서와 같이 테스트데이터에서도 좋은 성능을 내는 모델 : 일반화가 잘 된 모델
- 과적합(Over-fitting) : 모델이 훈련데이터에만 특수한 성질을 과하게 학습해 일반화를 못해 결국 테스트데이터에서 오차가 커지는 현상
- 과소적합(Under-fitting) : 훈련데이터에 과적합도 못하고 일반화 성질도 학습하지 못해 훈련/테스트 데이터 모두에서 오차가 크게 나오는 경우
분산/편향 트레이드 오프
- 분산이 높은 경우 : 모델이 학습 데이터의 노이즈에 민감하게 적합하여 테스트데이터에서 일반화를 잘 못하는 경우, 과적합
- 편향이 높은 경우 : 모델이 학습 데이터에서 특성과 타겟 변수의 관계를 잘 파악하지 못한 경우, 과소적합
독립변수와 종속변수가 비선형관계인 모델로 학습을 해야 하는 데이터에서,
1) 단순선형모델로 학습하는 경우와
2) 데이터 포인트를 모두 지나가도록 곡선 피팅이 가능한 다항모델로 학습을 진행한다고 가정
선형모델 예측은 학습데이터에서 타겟값과 오차가 큽니다. 이를 "편향(Bias)이 높다"고 합니다.(과소적합)
하지만 훈련/테스트 두 데이터에서 그 오차가 비슷합니다 이를 "분산이 낮다"고 합니다. (오차는 여전히 많지만)
곡선을 피팅한 모델에서는, 학습데이터에서 오차가 0에 가까우나("낮은 편향"), 테스트 데이터에서 오차가 많아집니다.이렇게 한 데이터세트에서는 오차가 적은데 다른 데이터 세트에서는 오차가 많이 늘어나는 현상
(데이터 세트의 종류에 따라 예측값 분산이 높을 때)을 과적합이라고 하며 "분산이 높다"라고 합니다.
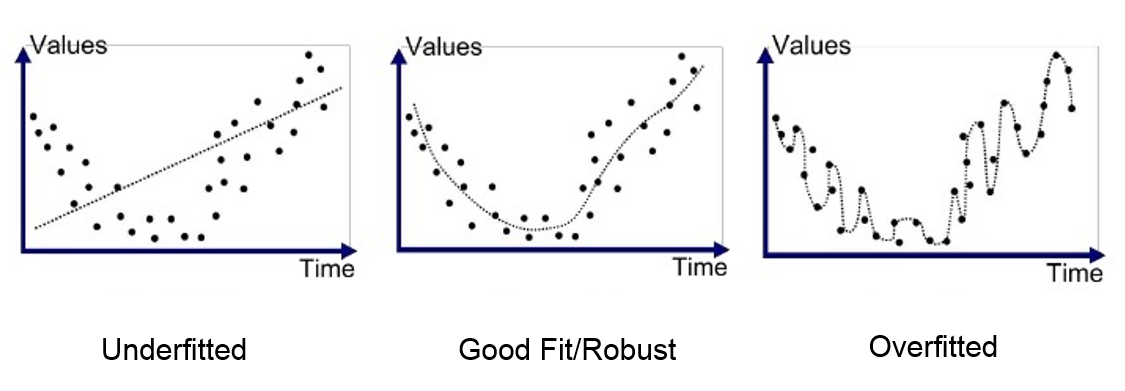

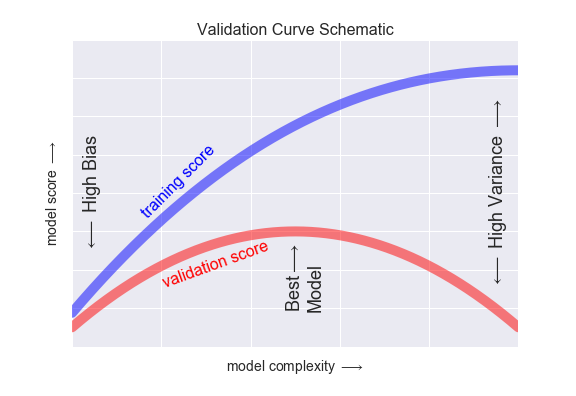
- validation score 낮아지는 지점 = 과적합이 일어나는 시점
Day 3
Ridge Regression
One-Hot encoding
문자열데이터(범주형)를 다루기 위한 기법
- 문자열데이터를 그대로 모델에 넣으면 오류가 발생해 인식하지 못함 --> 숫자로 변환 필요
- 1 or 0 으로 변환
- 범주의 개수가 너무 많으면 (= high cardinality) 사용하기 불편

category_encoders
Feature selection
과적합을 줄이는 방법 : 모델의 복잡도 낮추기 -> 독립변수의 수 ↓
-> 일부만 사용 = 독립변수 선택 : SelectKBest
# target(Price)와 가장 correlated 된 features 를 k개 고르는 것이 목표입니다.
## f_regresison, SelectKBest
from sklearn.feature_selection import f_regression, SelectKBest
## selctor 정의합니다.
selector = SelectKBest(score_func=f_regression, k=10)
## 학습데이터에 fit_transform
X_train_selected = selector.fit_transform(X_train, y_train)
## 테스트 데이터는 transform
X_test_selected = selector.transform(X_test)
all_names = X_train.columns
## selector.get_support()
selected_mask = selector.get_support()
## 선택된 특성들
selected_names = all_names[selected_mask]
## 선택되지 않은 특성들
unselected_names = all_names[~selected_mask] # features를 몇 개 선책하는 것이 좋은지 알아 봅시다.
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, r2_score
training = []
testing = []
ks = range(1, len(X_train.columns)+1)
# 1 부터 특성 수 만큼 사용한 모델을 만들어서 MAE 값을 비교 합니다.
for k in range(1, len(X_train.columns)+ 1):
print(f'{k} features')
selector = SelectKBest(score_func=f_regression, k=k)
X_train_selected = selector.fit_transform(X_train, y_train)
X_test_selected = selector.transform(X_test)
all_names = X_train.columns
selected_mask = selector.get_support()
selected_names = all_names[selected_mask]
print('Selected names: ', selected_names)
model = LinearRegression()
model.fit(X_train_selected, y_train)
y_pred = model.predict(X_train_selected)
mae = mean_absolute_error(y_train, y_pred)
training.append(mae)
y_pred = model.predict(X_test_selected)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
testing.append(mae)
print(f'Test MAE: ${mae:,.0f}')
print(f'Test R2: {r2} \n')
plt.plot(ks, training, label='Training Score', color='b')
plt.plot(ks, testing, label='Testing Score', color='g')
plt.ylabel("MAE ($)")
plt.xlabel("Number of Features")
plt.title('Validation Curve')
plt.legend()
plt.show()Ridge Regression ( = L2 Regression)
기존 다중회귀선을 훈련데이터에 덜 적합되도록 만들어 더 좋은 모델로 만드는 것
:
n: 샘플수, p: 특성수, : 튜닝 파라미터(패널티)
참고: alpha, lambda, regularization parameter, penalty term 모두 같은 뜻
- : 조절모수, 회귀추정치와 관련된 항의 영향을 조절해주는 역할
-> 교차검증을 통해 효율적으로 구할 수 있음 =RidgeCV
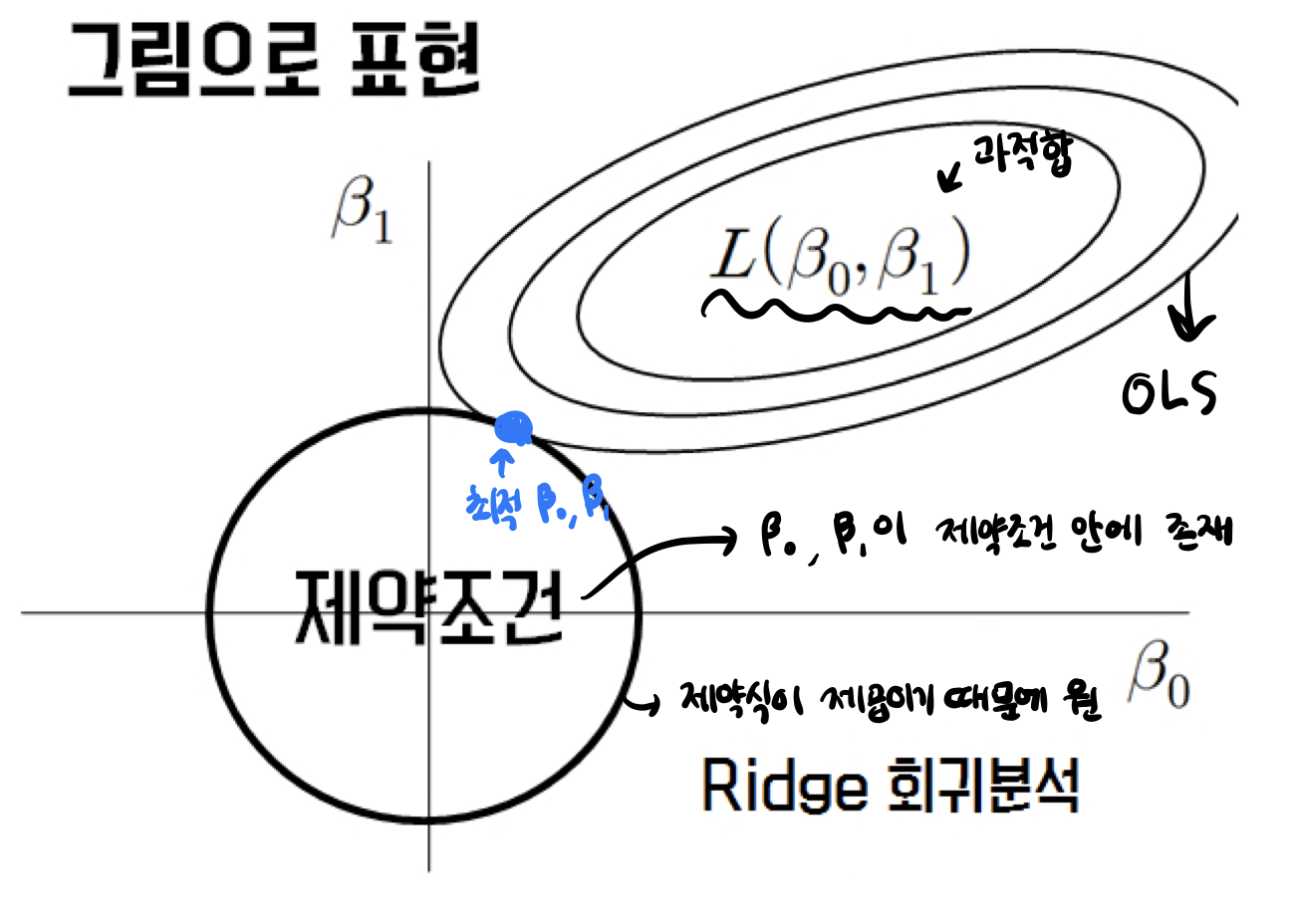
Ridge 회귀를 사용하는 이유
- Ridge 회귀는 과적합을 줄이기 위해서 사용
과적합을 줄이는 간단한 방법 중 한 가지는 모델의 복잡도를 줄이는 것
특성의 갯수를 줄이거나 모델을 단순한 모양으로 적합하는 것Ridge 회귀는 편향을 조금 더하고, 분산을 줄이는 방법으로 정규화(Regularization)를 수행
여기서 말하는 정규화는 모델을 변형하여 과적합을 완화해 일반화 성능을 높여주기 위한 기법을 의미정규화의 강도를 조절해주는 패널티값인 람다는
- → 0, →
- → ∞, → 0 : 클수록 릿지회귀계수 추정치 0에 가까워짐, 클수록 독립변수의 개수 감소
RidgeCV 를 통한 최적 패널티(alpha, lambda) 검증
from sklearn.linear_model import RidgeCV
alphas = [0.01, 0.05, 0.1, 0.2, 1.0, 10.0, 100.0]
ridge = RidgeCV(alphas=alphas, normalize=True, cv=3)
ridge.fit(ans[['x']], ans['y'])
print("alpha: ", ridge.alpha_)
print("best score: ", ridge.best_score_)- Ridge 회귀 직선은 OLS와 매우 비슷하게 생겼지만 Outlier에 영향을 덜 받음
- Ridge 회귀는 정규화를 통해 특이값으로 인한 과도한 기울기를 보정
- 또한 영향력이 낮은 특성의 회귀계수의 값을 감소시켜 특징선택 효과
Day 4
Logistic Regression
warm upTesting : all about checking performance good enough
Validation : allowing for redeemption, it's way to improve performance before you get to final exam
-> Need both in a machine learning
- test data로 예측 -> 수정 -> 예측 -> ... 반복X = 과적합 발생 有
training set = 모델을 fit하는데 사용
validation set = 예측모델을 선택하기 위해 예측오류를 측정할 때 사용
testing set = 일반화 오류를 평가하기 위해 선택된 모델에 한하여 마지막에 한번 사용
모델 검증
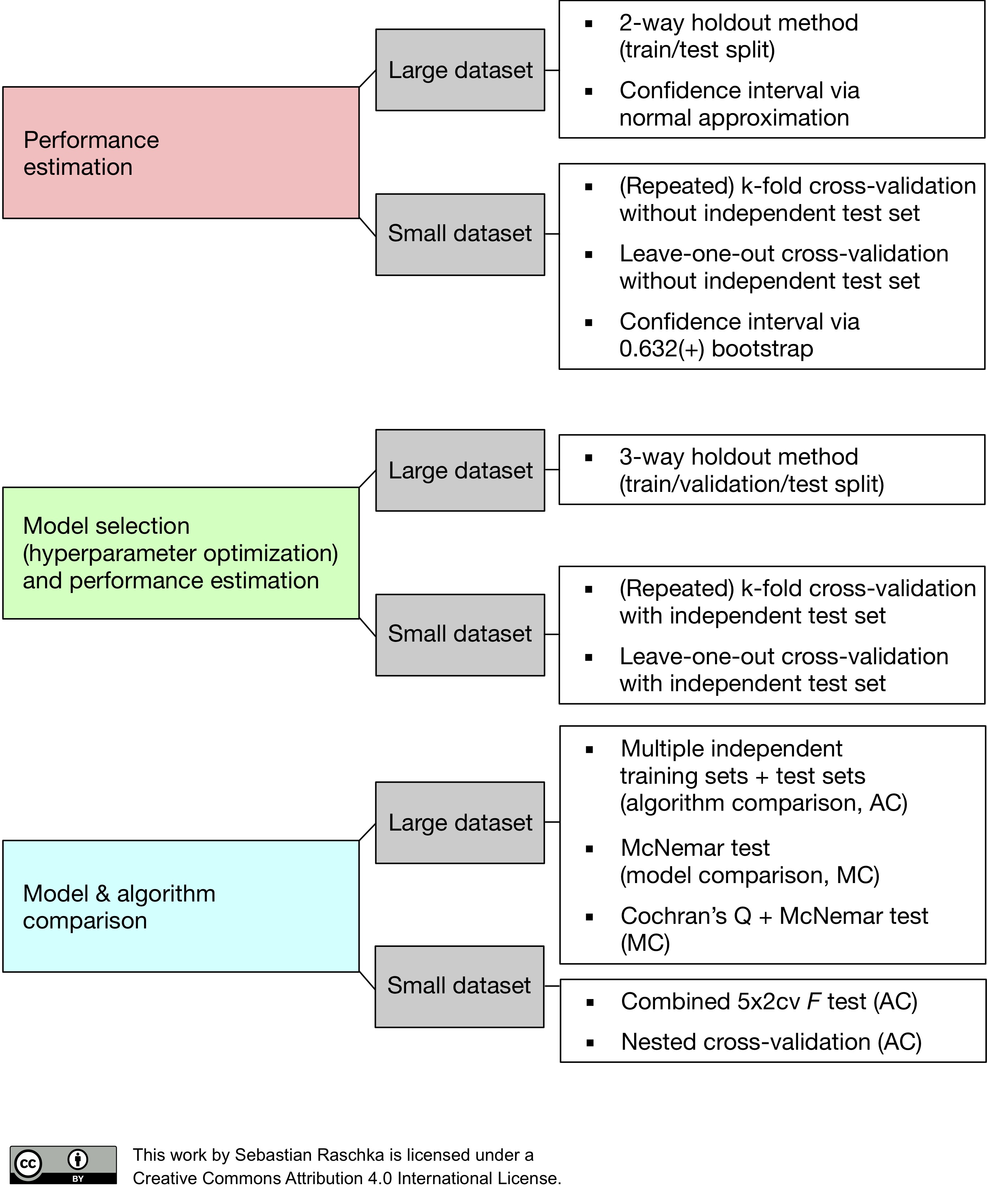
분류문제
분류문제 에서는 타겟 변수가 편중된 범주비율을 가지는 경우 多
클래스 1과 0 비율이 9:1인 학습 데이터를 가지고 모델을 만들었는데 모델 예측 정확도가 90%
- 불균형한 데이터를 사용해 ML 모델을 만드는데는 상당한 주의가 필요
- 이 데이터는 모델이 무조건 클래스 1만 찍도록 만들면 정확도 90%를 달성할 수 있음
- 이 경우 클래스 1에 대한 정확도가 90% 인 기준모델을 설정하고 더 좋은 성능을 가지는 모델을 만들기 위해 노력해야 함
- 분류문제를 풀기 전, 항상 타겟 범주가 어떤 비율을 가지고 있는지 확인 필요
# 기준모델
# mode(): Return the highest frequency value in a Series.
major = y_train.mode()[0]
# 타겟 샘플 수 만큼 0이 담긴 리스트를 만듭니다. 기준모델로 예측
y_pred = [major] * len(y_train)평가지표
scikit-learn, Scoring functions
- 정확도(Accuracy) 는 분류문제에서 사용하는 평가지표, Accuracy = =
- Proportion of correct classifications
# 최다 클래스의 빈도가 정확도가 됩니다.
from sklearn.metrics import accuracy_score
print("training accuracy: ", accuracy_score(y_train, y_pred))Logistic Regression
from sklearn.linear_model import LinearRegression
linear_model = LinearRegression()
# 숫자형 특성 만 사용하겠습니다.
features = ['Pclass', 'Age', 'Fare']
X_train = train[features]
X_val = val[features]
# Age, Cabin의 결측치를 평균 값으로 채웁니다.
from sklearn.impute import SimpleImputer
## default, imputing 'mean' value
imputer = SimpleImputer()
X_train_imputed = imputer.fit_transform(X_train)
X_val_imputed = imputer.transform(X_val)
# 학습
linear_model.fit(X_train_imputed, y_train)
# 예측
pred = linear_model.predict(X_val_imputed)로지스틱 회귀모델
,
로지스틱회귀는 특성변수를 로지스틱 함수 형태로 표현
-
결과적으로 관측치가 특정 클래스에 속할 확률값으로 계산
-
분류문제에서는 확률값을 사용하여 분류를 하는데, 예를들어 확률값이 정해진 기준값 보다 크면 1 아니면 0 이라고 예측
Logit transformation
- 로지스틱회귀의 계수는 비선형 함수 내에 있어서 직관적으로 해석하기가 어려운데 오즈(Odds) 를 사용하면 선형결합 형태로 변환 가능해 보다 쉽게 해석이 가능
- 오즈는 실패확률에 대한 성공확률의 비
ex) odds = 4 이면 성공확률이 실패확률의 4배 라는 뜻 - 분류문제에서는 클래스 1 확률에 대한 클래스 0 확률의 비라고 해석
,
p = 성공확률, 1-p = 실패확률
p = 1 일때 odds =
p = 0 일때 odds = 0
-
오즈에 로그를 취해 변환하는 것을 로짓변환(Logit transformation)
-
로짓변환을 통해 비선형형태인 로지스틱함수형태를 선형형태로 만들어 회귀계수의 의미를 해석
-
특성 X의 증가에 따라 로짓(ln(odds))가 얼마나 증가(or감소)했다고 해석
-
odds 확률로 해석을 하려면 exp(계수) = p 를 계산해서 특성 1단위 증가당 확률이 p배 증가한다고 해석
기존 로지스틱형태의 y 값은 0~1의 범위를 가졌다면 로짓은 - ~ 범위

- 카테고리 데이터 처리를 위해 OneHotEncoder
- 결측치(missing value) 처리를 위한 SimpleImputer
- 특성들의 척도를 맞추기 위해 표준정규분포로 표준화하는(평균=0, 표준편차=1) StandardScaler