
Day 1
Hypothesis test
기술 통계치(Descriptive Statistcs)의 시각화
- boxplot

- bagplot
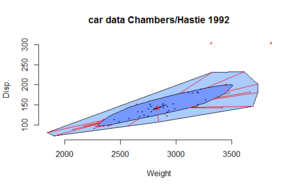
- violin plot
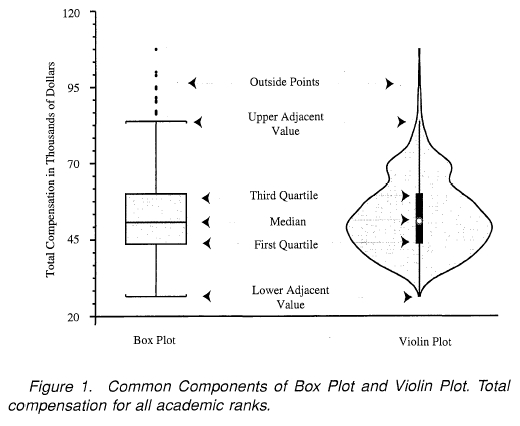
- Mean / Median / Mode
- Range
- Var / SD
- Kurtosis
- Skewness
추리 통계치(Inferential Statistics)

- Population
- Parameter
- Statistic
- Estimator
- Standard Deviation
- Standard Error
Effective Sampling
- Simple Random Sampling
모집단에서 sampling을 무작위로 하는 방법

- Systematic Sampling
모집단에서 sampling을 할 때 규칙을 가지고 추출하는 방법
ex) 1, 6, 11, 16, ... 번째의 데이터를 선택

- Stratified Random Sampling
모집단을 미리 여러 그룹으로 나누고, 그 그룹별로 무작위 추출을 수행하는 방법
ex) 여론 조사를 위해 사람을 나이대 별로 나누고, 해당 그룹안에서 무작위 추출
- Cluster Sampling
모집단을 미리 여러 그룹으로 나누고, 이후 특정 그룹을 무작위로 선택하는 방법

가설검정
- 주어진 상황에 대해서, 하고자 하는 주장이 맞는지 아닌지를 판정하는 과정.
- 모집단의 실제 값에 대한 sample의 통계치를 사용해서 통계적으로 유의한지 아닌지 여부를 판정함.
- 표본 수가 더욱 많아질수록 추측은 더 정확해지고 높은 신뢰도를 바탕으로 모집단에 대한 예측을 할 수 있도록 함
- One sample t-test
1개의 sample값들의 평균이 특정값과 동일한지 비교
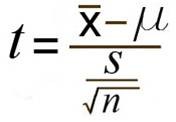
- 위 통계치는, 평균을 빼고, 표준편차로 나눠줬는데 이러한 과정을 정규화라고 하며, 이 과정을 하게 되면 주어진 데이터가 평균은 0, 표준편차가 1인 데이터로 scaling이 된다.
-
Process
- 귀무가설(Null Hypothesis) 설정 :
- 대안 가설 (Alternative Hypothesis) 설정 :
- 신뢰도(Confidece Level) 설정 : 모수가 신뢰구간 안에 포함될 확률
신뢰도 95% = 모수가 신뢰구간 안에 포함될 확률 95% = 귀무가설이 틀렸지만 우연히 성립할 확률 5%

-
P-value 확인 : 주어진 가설에 대해서 "얼마나 근거가 있는지" 에 대한 값을 0과 1사이의 값으로 scale한 지표 = 일반화 해도 되는 기준점으로 작을수록 정확
P-value 낮음 = 귀무가설이 틀렸을 확률이 높다
P-value가 0.05 = 귀무가설이 틀렸지만 우연히 맞을 확률이 0.05
ex) p-value : 0.85 --> 귀무가설은 틀리지 않았다. (귀무가설이 옳다와 톤이 약간 다름) -
P-value 바탕으로 가설에 대한 결론 도출
-
Two sample t-test
2개의 sample값들의 평균이 서로 동일한지 비교
- Process
- 귀무가설 : 두 확률은 같다(차이가 없다) ->
- 대립가설 : 같지 않다 ->
자유도(Degree of Freedom)
주어진 조건하에서 통계적 제한을 받지 않고 자유롭게 변화할 수 있는 수
가정

- 독립성 : 두 그룹이 연결되어 있는 (paired) 쌍인지

- 등분산성 : 두 그룹이 어느정도 유사한 수준의 분산 값을 가지는지

- 정규성: 데이터가 정규성을 나타는지

즉 t-test는 특정한 조건에서 그룹의 평균을 비교하기 위한 가설검정 방법
Day 2
Chisquare test
Type of Error

- : 1종 오류 -> 참을 거짓으로 검정 =
- 유의수준 : 1종 오류를 범할 확률의 최대 허용 한계
- : 2종 오류 -> 거짓을 참으로 검정 =
- : 검정력(2종 오류를 감소시키면 검정력 증가) = 1 - =
test
- One sample test
Null hypothesis : 관측치는 집단/변수에 따라 차이가 없다.
Alter. hypothesis : 관측치는 집단/변수에 따라 차이가 있다.
- 표준화된 값을 위해
scipy의stats.chi2.cdf사용해 검정
- Two sample test
Null hypothesis : 두 변수 사이에 연관성이 없다.(독립적)
Alter. hypothesis : 두 변수 사이에 연관이 있다.
자유도
-
one sample (적합도 검정), DF = categories-1
-
two sample (독립성 검정), DF = (행 - 1)*(열 - 1)
Day 3
Confidence intervals
ANOVA(One-way)
2개 이상 그룹의 평균에 차이가 있는지 검정
F-statistic
- F값이 높다 = 분자(다른 그룹끼리의 분산)는 크고, 분모(전체 그룹의 분산)는 작음 = 그룹 간 평균차이가 있다 = Alter. 채택 확률 증가
공식
= 전체 그룹 수, = 데이터 수
=
큰 수의 법칙(Law of large numbers)
sample의 데이터의 수가 커질수록 sample의 통계치는 점점 모집단의 모수와 같아짐
중심극한정리(Central Limit Theorem, CLT)
sample 데이터의 수가 많아질수록 sample의 평균은 정규분포에 근사한 형태
신뢰도(Confidence Intervals, Cl)
신뢰도가 95%는 표본을 100번 뽑았을 때 95번은 신뢰구간 내에 모집단의 평균이 포함됨을 의미
공식 :
-
:
estimated mean -
:
error
Day 4
Bayesian
조건부 확률(The Law of Conditional Probability)
전체 사각형이 모든 가능한 확률 공간, 는 왼쪽 원, 는 오른쪽 원이며 그 교집합이 가운데 붉은 부분
위의 식에 를 양변에 곱하면, , 를 의미
- 라는 정보가 주어진 상황에서 의 확률은 와 교집합들의 합으로 구성 되어 있음
베이지안 이론
,
Since
Therefore
=
- 가 주어진 상황에서 의 확률은 가 주어진 상황에서의 의 확률 곱하기 의 확률, 나누기 의 확률로 표현
-> 사후 확률. (B라는 정보가 업데이트 된 이후의 사(이벤트)후 확률)
-> 사전 확률. B라는 정보가 업데이트 되기 전의 사전확률
-> data
- 조건이 붙지 않은 확률 은 사전확률("Prior"), 조건이 붙은 부분은 사후확률("Updated")
