Monte Carlo Simulation - Estimating Pi

What is Monte Carlo Method?

a computational algorithms that rely on repeated random samplings to obtain numerical results.

Calculating the Pi using the Monte Carlo Method

Monte Carlo Simulation is often used to estimate the value of π = 3.1415926535897....

1. Assume there is a circle of radius 1

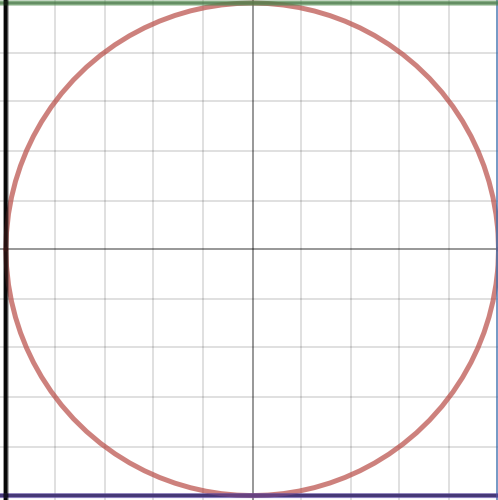
2. Divide the Cirlce into quarter

Since area of circle equals πr^2, the area of the quarter-circle above will be π/4.

Assuming throwing N-darts to the quarter-square and that M-darts were within the circle, π can be estimated by the following equation.

			π / 4 = M / N
            		π = (M / N) * 4
                    

Code (C++)

#include <iostream>
#include <stdlib.h>

double x = 0;
double y = 0;
double total = 0; // total attempts of dots
double inCircle = 0; // total dots within the circle

int main()
{
    while(1)
    {
        for (double i = 0; i <= 100000000000; i++)
        {
            x = (double)rand() / (double)RAND_MAX;
            y = (double)rand() / (double)RAND_MAX;

            total++;

            if ((x * x) + (y * y) <= 1)
                inCircle++;
            

            printf("total = %0.0f, pi = %0.15f\n", total, (inCircle / total) * 4);
        }
    }
}

Output

total = 2625096, pi = 3.140301154700628
total = 2625097, pi = 3.140301482192848
total = 2625098, pi = 3.140300285932182
total = 2625099, pi = 3.140300613424484
total = 2625100, pi = 3.140300940916537
total = 2625101, pi = 3.140301268408339
total = 2625102, pi = 3.140301595899893
total = 2625103, pi = 3.140301923391196
total = 2625104, pi = 3.140302250882251
total = 2625105, pi = 3.140302578373055
total = 2625106, pi = 3.140302905863611
total = 2625107, pi = 3.140303233353916
total = 2625108, pi = 3.140302037097140
total = 2625109, pi = 3.140302364587527
total = 2625110, pi = 3.140302692077665
total = 2625111, pi = 3.140301495822462
total = 2625112, pi = 3.140300299568171

By using the equation deduced above, random numbers - x and y succesfully estimate the approximation of π.