Sieve of Eratosthenes in Code

What is Sieve of Eratosthenes?

The sieve of Eratosthenes is an ancient algorithm for finding all the prime numbers to the given limit by excluding the multiples of the prime numbers (ex- 2,3,5,7)

How to Find Prime Numbers from 1 - 100

1. First Write Down From Number 1 - 100

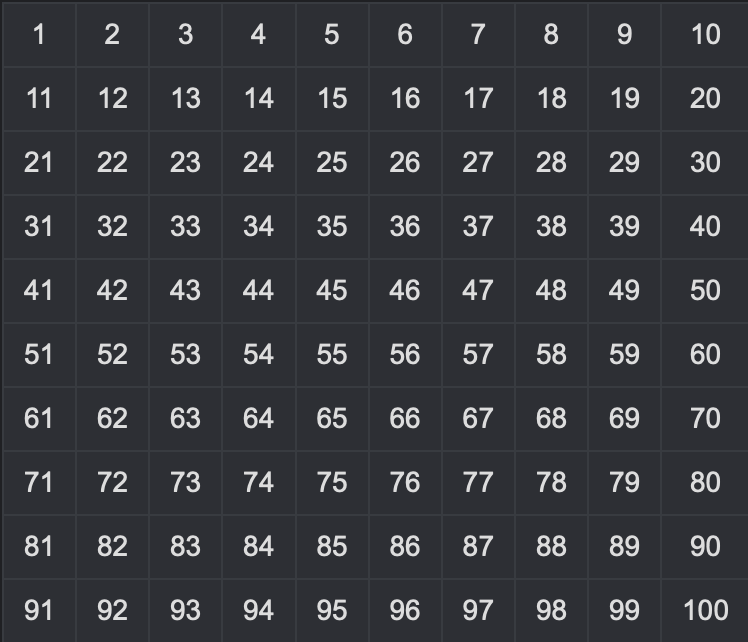
2. Remove 1 (since number 1 is neither compound nor prime number)

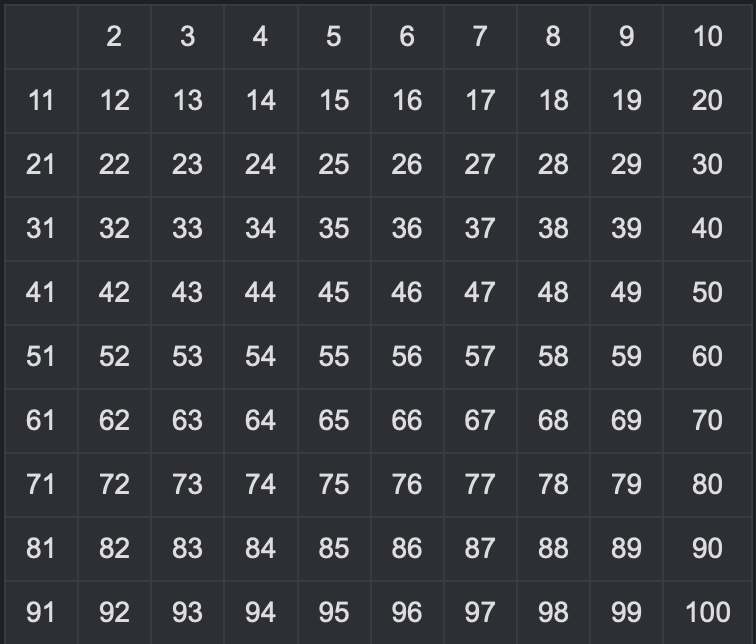
3. Remove Multiples of 2 Excluding 2

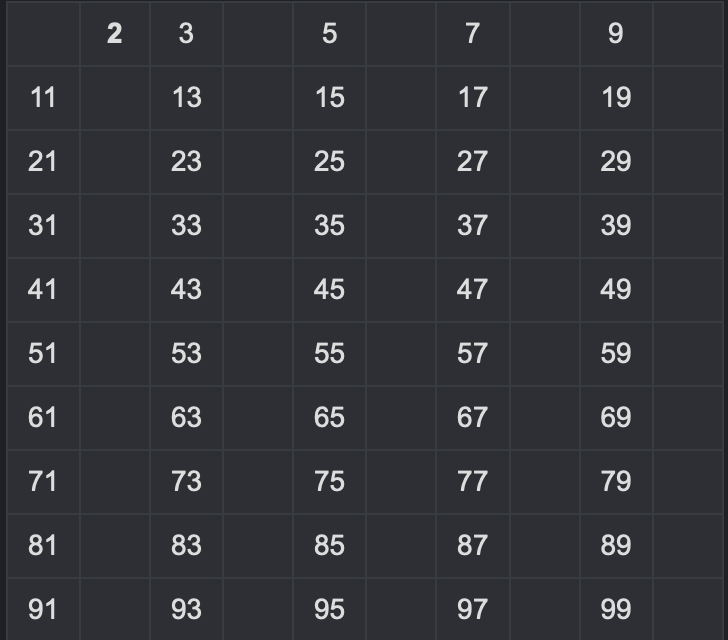
4. Remove Multiples of 3 Excluding 3

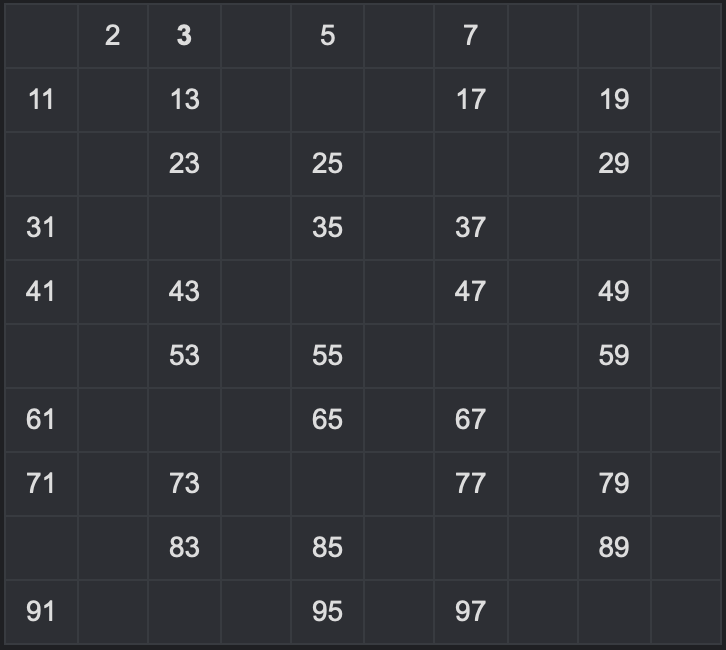
5. Remove Multiples of 5 Excluding 5

Since the multiples of 4 are already removed, resume to next smallest prime number 5.

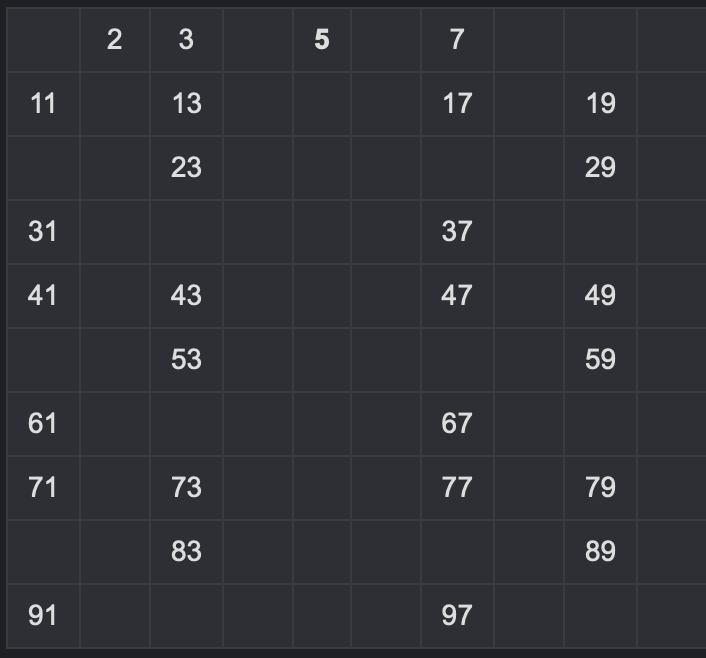
5. Remove Multiples of 7 Excluding 7

The next smallest prime number 11 is greater than the sqrt(100), therefore the process ceases.

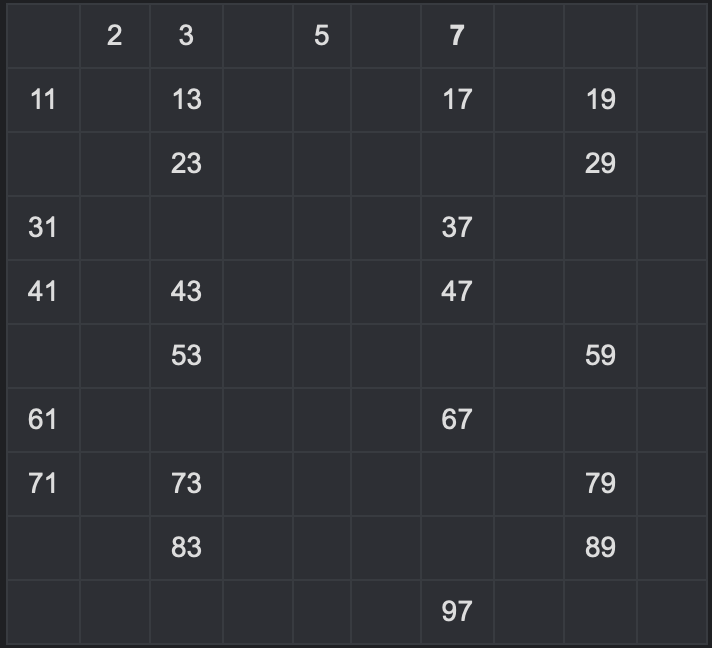
6. Result

List of Prime Numbers from 1 - 100
result = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

Sieve of Eratosthenes in C++

Code

#include <iostream>
#include <math.h>
using namespace std;

int N;
int D; 
int total = 0;

int main()
{
    cin >> N;

    bool* isPrime = new bool[N];
    D = sqrt(N);

    for (int i = 1; i < N; i++)
    {
        isPrime[i] = true;
    }

    for (int i = 2; i <= D; i++)
    {
        if (isPrime[i] == true)
            for (int j = i + i; j < N; j = j + i)
            {
                isPrime[j] = false;
            }
    }

    for(int i = 2; i < N; i++)
    {
        if (isPrime[i] == true)
        {
            cout << i << ", ";
            total = total + 1;
        }
    }
    cout << endl;

    cout << "# of Primes : " << total << endl;

    return 0;
}

Output

100
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 
# of Primes : 25

Sieve of Eratosthenes in Python

Code

def isPrime():
    N = int(input())
    sieve = [True] * N
 
    limit = int(N ** 0.5)
    for i in range(2, limit + 1):
        if sieve[i] == True:           
            for j in range(i+i, N, i):
                sieve[j] = False
 
    return [i for i in range(2, N) if sieve[i] == True]

print(isPrime())

Output

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]