Leetcode : Pascal's Triangle II
Description
Given an integer rowIndex, return the rowIndexth row of the Pascal's triangle.
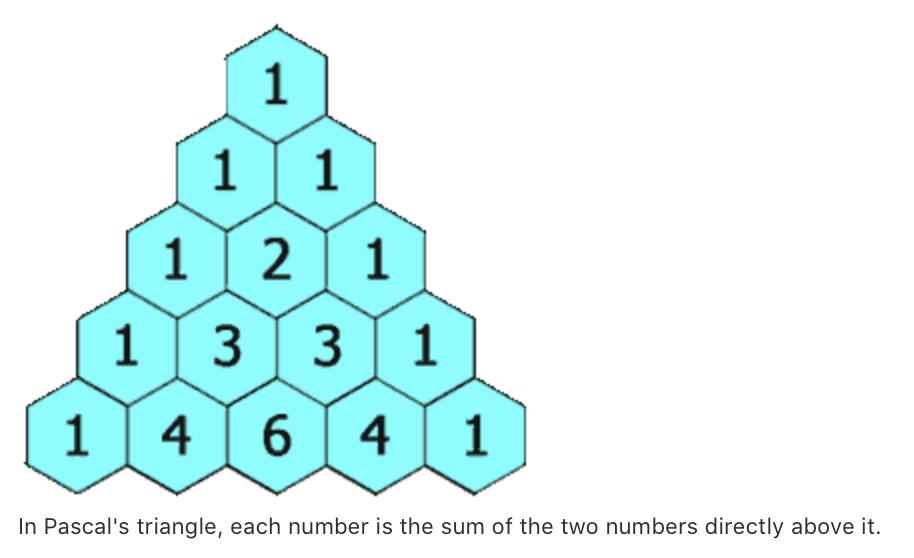
Example 1
Input
rowIndex = 3Output
[1,3,3,1]Example 2
Input
rowIndex = 0Output
[1]Example 3
Input
rowIndex = 1Output
[1,1]Approach
Find the relationship between the current index - i and the previous index - i - 1 (i.e- dynamic programming)
Solutions
Solution 1 (Python)
class Solution(object):
def getRow(self, rowIndex):
result = []
for i in range(0, rowIndex+1):
result.append([])
for j in range(0, i + 1):
if j == 0:
result[i].append(1)
elif i == j:
result[i].append(1)
else:
result[i].append((result[i-1][j-1]) + (result[i-1][j]))
return result[rowIndex]Result
Runtime : 16ms
Memory Usage : 12.9MB
Runtime Beats 88.62% of Python Submission
Solution 2 (C++)
#include <iostream>
#include <vector>
using namespace std;
int N;
unsigned long long result[41][41];
int main()
{
cin >> N;
for (int i = 0; i <= N; i++)
{
for (int j = 0; j <= i; j++)
{
if (j == 0)
result[i][j] = 1;
else if (i == j)
result[i][j] = 1;
else
result[i][j] = (result[i-1][j-1]) + (result[i-1][j]);
}
}
for (int i = 0; i <= N; i++)
{
cout << result[N][i] << endl;
}
return 0;
}Solution 3 with Vector (C++)
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> result(rowIndex + 1, 1);
for (int i = 2; i <= rowIndex; i++)
{
for (int j = i - 1; j > 0; j--)
{
result[j] = result[j] + result[j-1];
}
}
return result;
}
};Result
Runtime : 0ms
Memory Usage : 6.4MB
Runtime Beats 100% of C++ Submission
