힙 정렬(Heap Sort)

힙 정렬(Heap Sort)은 완전 이진 트리를 기반으로 하는 힙(Heap) 자료구조를 활용한 정렬 알고리즘이다. 주로 최대값 또는 최소값을 빠르게 찾아야 하는 문제에서 유용하게 활용된다. 힙 정렬은 불안정 정렬(Unstable Sort)이며, 평균, 최선, 최악의 시간 복잡도는 O(n log n)이다.

---

완전 이진 트리와 힙의 개념

• 완전 이진 트리: 삽입할 때 왼쪽부터 차례대로 노드를 추가하는 이진 트리.
• 최대 힙(Max Heap): 부모 노드의 값이 항상 자식 노드의 값보다 크거나 같은 구조.
• 최소 힙(Min Heap): 부모 노드의 값이 자식 노드의 값보다 작거나 같은 구조.

---

힙 정렬의 동작 과정

1. 최대 힙 구성
   배열을 기반으로 최대 힙을 구성한다.
   아래 그림은 초기 배열에서 최대 힙이 구성되는 과정을 시각적으로 보여준다.
   

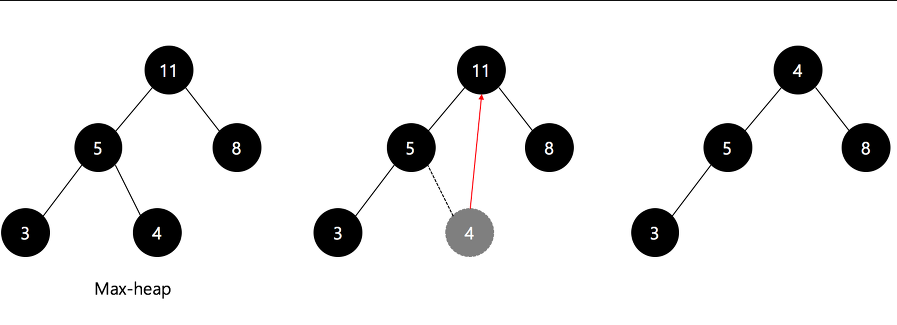
• 설명: 첫 번째 이미지는 최대 힙(Max-Heap)이 구성되는 과정을 단계적으로 시각화해준다. 루트 노드와 자식 노드 간 값을 교환하며 최대 힙을 구성하는 과정이 직관적으로 드러난다.

2. 요소 교환과 힙 재구성
   루트 노드(최대값)를 마지막 요소와 교환하고, 힙 크기를 줄인 뒤 다시 최대 힙을 구성한다.
   아래 그림은 루트와 마지막 노드를 교환한 후 힙을 재구성하는 과정을 보여준다.
   

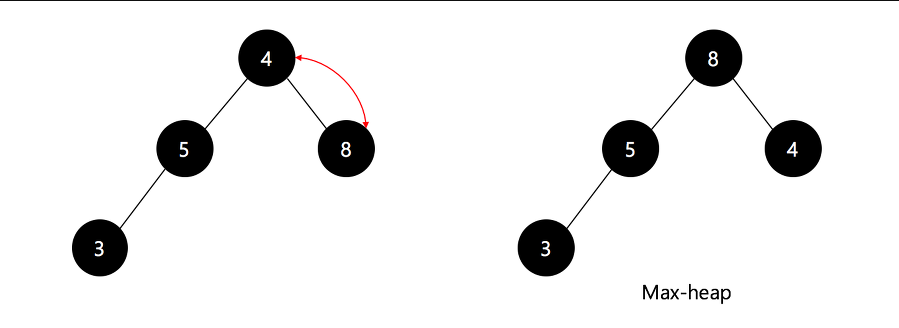
• 설명: 두 번째 이미지는 루트 노드와 마지막 노드 교환 후 최대 힙을 재구성하는 단계를 시각적으로 표현한다. 재구성 과정에서 부모-자식 간 값을 교환하며 힙 속성이 유지되는 모습을 보여준다.

3. 최대값 추출 및 정렬
   루트 노드(최대값)를 마지막 요소와 교환하고, 힙 크기를 줄인 뒤 다시 힙을 구성한다.

4. 반복 처리
   힙 크기가 1이 될 때까지 위 과정을 반복하며 정렬을 완료한다.

---

힙 정렬 구현

public class HeapSort {
    public static void main(String[] args) {
        int[] array = {230, 10, 60, 550, 40, 220, 20};

        heapSort(array);

        for (int value : array) {
            System.out.print(value + " ");
        }
    }

    // 힙 정렬 메서드
    public static void heapSort(int[] array) {
        int n = array.length;

        // 초기 힙 구성
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(array, n, i);
        }

        // 힙에서 최대값 추출 후 정렬
        for (int i = n - 1; i > 0; i--) {
            swap(array, 0, i);  // 최대값을 마지막으로 이동
            heapify(array, i, 0);  // 힙 재구성
        }
    }

    // 힙 구성 메서드
    public static void heapify(int[] array, int n, int i) {
        int parent = i; // 부모 노드 인덱스
        int left = 2 * i + 1; // 왼쪽 자식
        int right = 2 * i + 2; // 오른쪽 자식

        // 왼쪽 자식이 더 크다면 부모와 교체
        if (left < n && array[parent] < array[left]) {
            parent = left;
        }

        // 오른쪽 자식이 더 크다면 부모와 교체
        if (right < n && array[parent] < array[right]) {
            parent = right;
        }

        // 부모 노드가 자식 노드보다 작다면 스왑 후 재귀 호출
        if (i != parent) {
            swap(array, i, parent);
            heapify(array, n, parent);
        }
    }

    // 배열 요소 교환 메서드
    public static void swap(int[] array, int a, int b) {
        int temp = array[a];
        array[a] = array[b];
        array[b] = temp;
    }
}

---

구현 방식 설명

1. 힙 구성 단계

• 부모 노드와 자식 노드 간의 값을 비교해 최대 힙(또는 최소 힙)을 구성한다.
• 인덱스 기반으로 왼쪽 자식은 2 i + 1, 오른쪽 자식은 2 i + 2로 접근한다.

2. 요소 교환과 힙 재구성

• 루트 노드(최대값)를 배열 끝으로 이동한 뒤, 힙 크기를 줄이고 다시 최대 힙을 구성한다.

---

힙 정렬의 특징과 활용

특징

• 장점

  • 정렬 과정에서 추가 메모리가 필요하지 않다.
  • 특정 상황에서 안정적 성능을 제공한다.

• 단점

  • 퀵 정렬이나 합병 정렬에 비해 구현이 복잡하다.
  • 실제 사용 사례는 퀵 정렬, 합병 정렬보다 적다.

활용

• 최대값/최소값 찾기

  • 최대 힙이나 최소 힙을 통해 한 번의 연산으로 가장 크거나 작은 값을 빠르게 구할 수 있다.

• k-인근 요소 정렬

  • 특정 범위 내에서 정렬하는 문제에서 효율적인 결과를 제공한다.

So...

힙 정렬은 힙 자료구조의 개념을 기반으로 효율적인 정렬을 제공하지만, 구현의 복잡성으로 인해 다른 정렬 알고리즘에 비해 실무 활용 빈도는 낮다. 그러나 힙 자료구조가 다양한 문제 해결에 활용되는 만큼, 이를 이해하는 과정에서 힙 정렬은 매우 중요한 개념이다. 특히, 대용량 데이터의 특정 연산을 빠르게 처리해야 하는 상황에서 유용하다.