기능개발 (스택/큐)

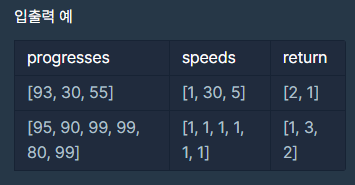
입출력 예는 위와 같다.
간단히 설명하면 progresses 리스트는 100% 중 진행도이다
93은 93%, 30은 30% 수행됐음을 뜻하며 , 각각 7% 70% 남은 상황이다
speeds배열은 작업 속도이며 93%의 경우 speed 1이니 남은 7%를 수행하는데
7일, 30%의 경우 3일, 이틀하고 3분의1일 ㅋ인것이다.
여기서 일단 바로 생각할 수 있는건 작업효율이 소수로 나눠질때
ceil()을 이용하면 된다는 것이다.
45% 남고 speed가 4일때 11.25 이면 12일 이 필요하고
75%남았는데 speed가 7이면 10.77 이니 11일이 필요하다
즉 올림으로 생각하면 된다.
그렇게해서 작업효율 리스트를 만들어서 보면
입출력예제 1,2를 표현해보자

eff1= [ 7 , 3 , 11 ]   - > [2,1]
eff2= [ 5, 10 , 1, 1, 20 ,1]   -> [ 1, 3, 2]
answer=[]
cnt=1 /cnt+=1로 가자/

tmp를 만들어서 대장을 만들어줄계획
일단 eff1에서 0번째 값 7이 대장이다
3은 7한테 진다 , 그니까 cnt+=1 여전히
대장 tmp는 7이다 . 11은 7보다 크다. 대장바꼈다.

쌓였던 cnt는 마무리해서 answer에 넣어주고 다시 1로 초기화
이게 메커니즘이다.
eff2도 마찬가지. eff2[0]=5가 대장으로 시작해서
바로 10한테 져서 cnt=1 answer에 넣어주고 10이 20전까지 2번 이기니
+1+1쌓여서 3돼서 answer에 3들어가고 20이 1이기고 2돼서 2넣어주니
[1,3,2]가 된다. 인덱스 범위만 안 벗어나게 잘 짜주면 끝~

import math
def solution(progresses, speeds):
    answer = []
    prog=[]
    for i in range(len(progresses)):
        prog.append(math.ceil((100-progresses[i])/speeds[i]))
    prog.append(0)
    print(prog)
    cnt = 1
    tmp = prog[0]
    for i in range(len(prog)-2):
        if prog[i+1]>tmp:
            tmp=prog[i+1]
            answer.append(cnt)
            cnt=1
            if (i + 1) == (len(prog) - 2):
                answer.append(cnt)
        elif prog[i+1]<=tmp:
            cnt+=1
            if (i + 1) == (len(prog) - 2):
                answer.append(cnt)
    return answer
progresses=[93, 30, 55]
speeds=[1, 30, 5]
print(solution(progresses,speeds))