💻 C++ 기반
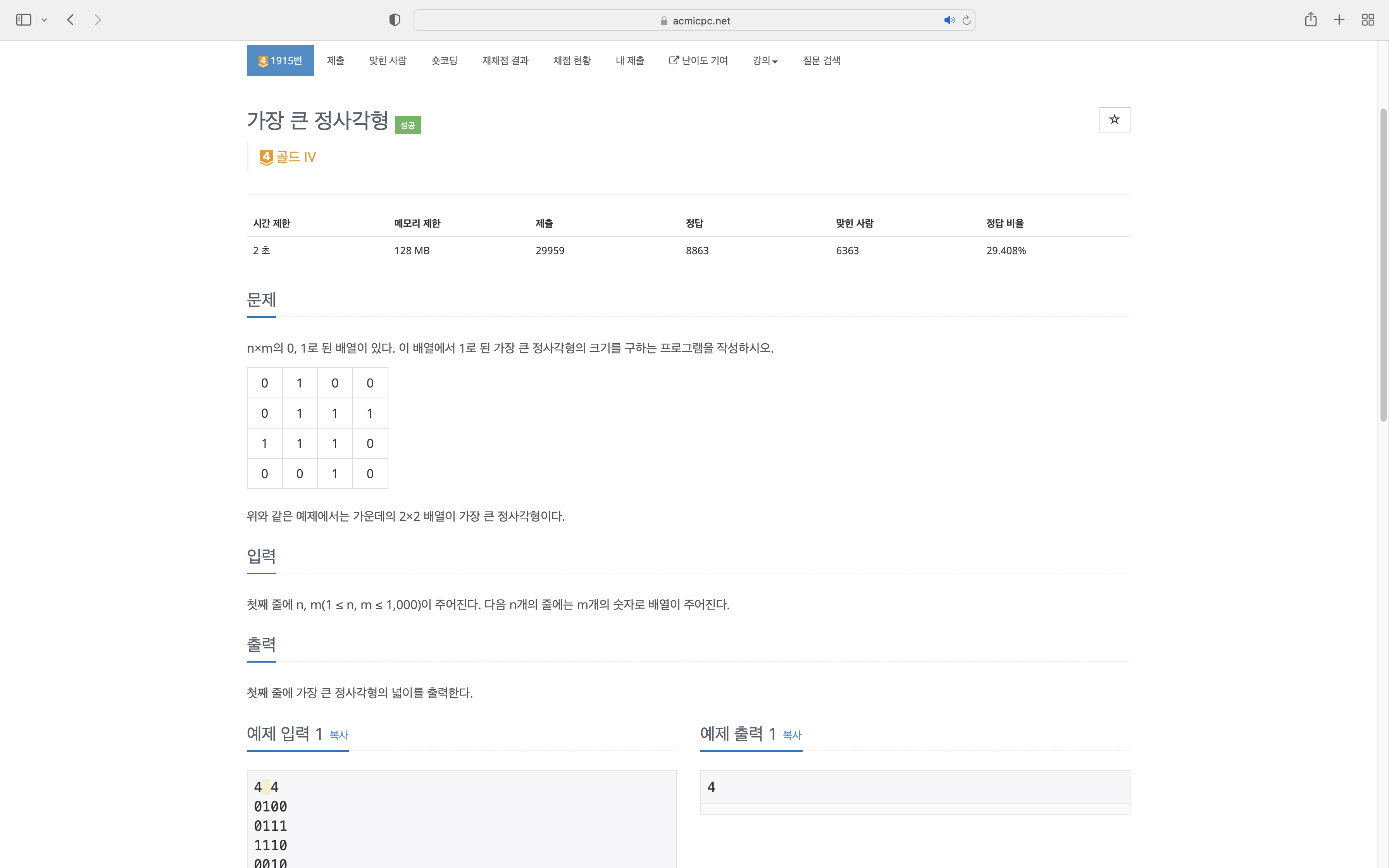
가장 큰 정사각형
https://www.acmicpc.net/problem/1915
✔️ 변의 길이가 1, 변의 길이가 2, … 이런 식으로 정사각형의 크기별로 1로 이루어져 있는지 다 확인하면 시간 초과 -> DP 활용 필요
1. 테이블 정의하기
dp[i][j]: (i, j)를 시작점으로 했을 때 만들 수 있는 '1로 이루어진 정사각형'의 한 변의 길이
2. 점화식 찾기
i) (0, 0)을 시작점으로 하는 2x2 정사각형은
(0, 0) | (0, 1)
(1, 0) | (1, 1)
시작점이 (0, 0)인 1x1 정사각형이 다 1로 이루어진지 확인
시작점이 (0, 1)인 1x1 정사각형이 다 1로 이루어진지 확인
시작점이 (1, 0)인 1x1 정사각형이 다 1로 이루어진지 확인
시작점이 (1, 1)인 1x1 정사각형이 다 1로 이루어진지 확인
ii) (0, 0)을 시작점으로 하는 3x3 정사각형은
(0, 0) | (0, 1) | (0, 2)
(1, 0) | (1, 1) | (1, 2)
(2, 0) | (2, 1) | (2, 2)
시작점이 (0, 0)인 2x2 정사각형이 다 1로 이루어진지 확인
시작점이 (0, 1)인 2x2 정사각형이 다 1로 이루어진지 확인
시작점이 (1, 0)인 2x2 정사각형이 다 1로 이루어진지 확인
시작점이 (1, 1)인 2x2 정사각형이 다 1로 이루어진지 확인
iii) (0, 0)을 시작점으로 하는 kxk 정사각형은
시작점이 (0, 0)인 (k-1)x(k-1) 정사각형이 다 1로 이루어진지 확인
시작점이 (0, 1)인 (k-1)x(k-1) 정사각형이 다 1로 이루어진지 확인
시작점이 (1, 0)인 (k-1)x(k-1) 정사각형이 다 1로 이루어진지 확인
시작점이 (1, 1)인 (k-1)x(k-1) 정사각형이 다 1로 이루어진지 확인
-> kxk 정사각형이 만들어지는 시작점이 (0, 0)일 때부터 (n-k, m-k)가 될 때까지 위 과정 반복
3. 초기값 정하기
1x1 정사각형이 1로 이루어져 있으면 dp[i][j] = 1
#include <iostream>
#include <string>
#include <algorithm>
#define MAX 1001
using namespace std;
int board[MAX][MAX];
int dp[MAX][MAX];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n, m;
cin >> n >> m;
for (int i = 0; i < n; i++)
{
string input;
cin >> input;
for (int j = 0; j < m; j++)
{
board[i][j] = input[j] - '0';
if (board[i][j] == 1)
{
dp[i][j] = 1;
}
}
}
int side = 2;
while (side <= m && side <= n)
{
for (int i = 0; i <= n - side; i++)
{
for (int j = 0; j <= m - side; j++)
{
if (dp[i][j] == side - 1 && dp[i][j + 1] == side - 1 && dp[i + 1][j] == side - 1 && dp[i + 1][j + 1] == side - 1)
{
dp[i][j] = side;
}
}
}
side++;
}
int maximum = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
maximum = max(maximum, dp[i][j]);
}
}
cout << maximum * maximum;
return 0;
}