배열과 연결 리스트를 비교하며 보자
둘다 선형 자료구조
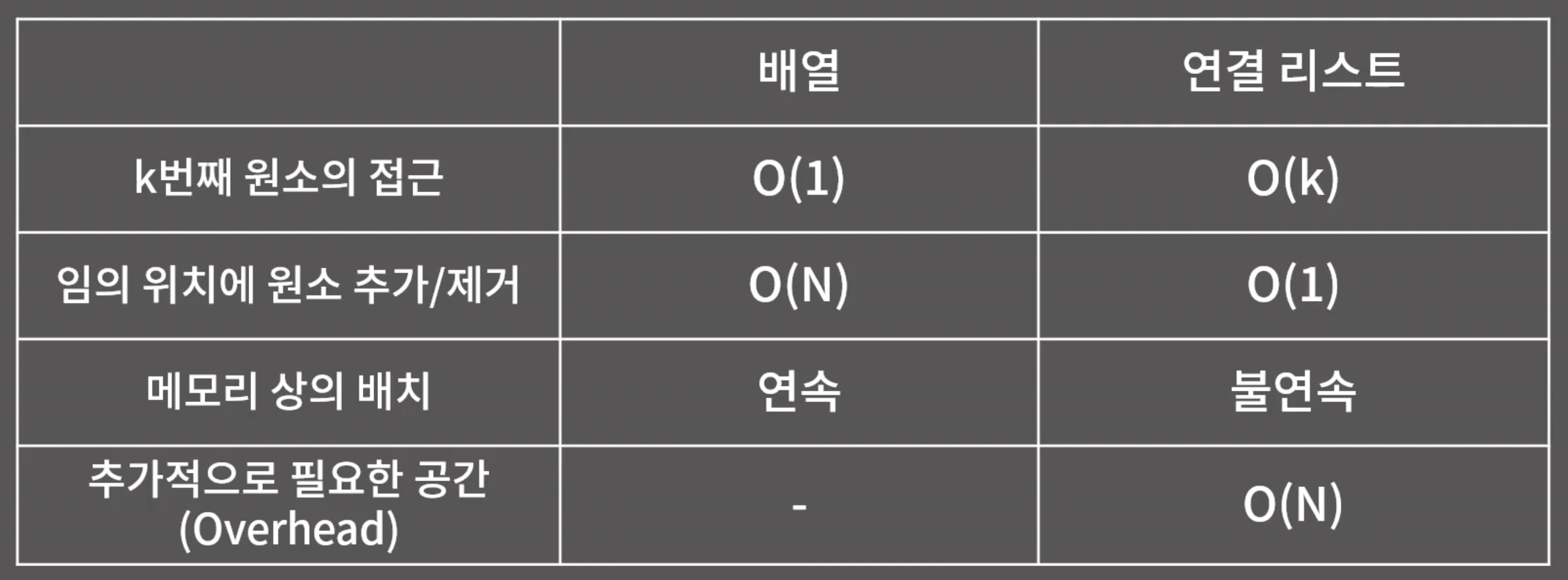
연결 리스트의 성질
- 임의의 위치에 있는 원소를 확인/변경하기 위해 O(N)가 필요함 📌배열은 O(1) 필요
- (주소가 주어졌을 때) 임의의 위치에 원소를 추가/임의 위치의 원소 제거는 O(1) -> 그 뒤의 원소들을 전부 옮기는 작업을 할 필요가 없고 다음 원소의 주소만 변경하면 됨 📌배열은 O(N) 필요
- 원소들이 메모리 상에 연속해있지 않아 Cache hit rate가 낮지만 할당이 다소 쉬움 📌배열은 높음

연결 리스트의 종류
- 단일 연결 리스트(Singly Linked List): 각 원소가 자신의 다음 원소의 주소를 들고 있는 리스트
- 이중 연결 리스트(Doubly Linked List): 각 원소가 자신의 이전 원소와 다음 원소의 주소를 둘다 들고 있는 리스트 -> 메로리를 더 씀
- 원형 연결 리스트(Circular Linked List): 끝이 처음과 연결 -> 단일 리스트와 이중 리스트 둘다 가능
연결 리스트의 예시
- 텍스트 에디터: 다양한 연산들이 다양하게 주어지고 최종 결과 출력
연결 리스트의 구현
const int MX = 1000005;
int dat[MX], pre[MX], nxt[MX];
int unused = 1;
fill(pre, pre+MX, -1);
fill(nxt, nxt+MX, -1);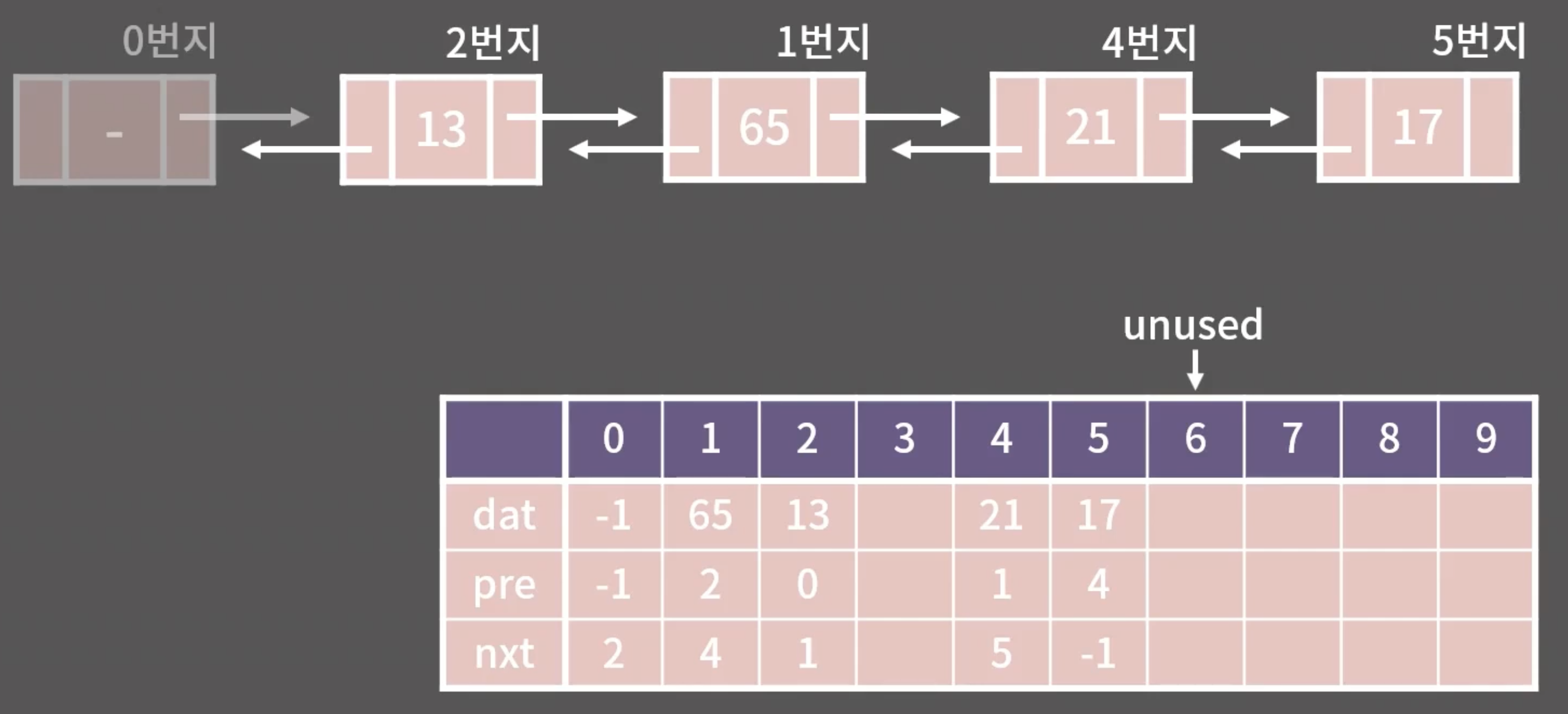
void traverse() {
int cur = nxt[0];
while(cur != -1) {
cout << dat[cur] << ' ';
cur = nxt[cur];
}
cout << "\n\n";
}
void insert(int addr, int num) {
dat[unused] = num;
pre[unused] = addr;
nxt[unused] = nxt[addr];
if (nxt[addr] != -1) pre[nxt[addr]] = unused;
nxt[addr] = unused;
unused++;
}
void erase_test(int addr) {
nxt[pre[addr]] = nxt[addr];
if (nxt[addr] != -1) pre[nxt[addr]] = pre[addr];
// dummy node 때문에 pre[addr]는 -1이 아님을 보장받음
}- 위 방식은 제거된 원소가 프로그램이 종료될 때까지 메모리를 점유하고 있어 실무에서는 사용 불가
- 코딩테스트에서는 insert의 횟수에 제한이 있으므로 배열을 그만큼 넉넉하게 잡아서 사용 가능
STL list
list<int> L = {1,2}; // 1 2
list<int>::iterator t = L.begin(); // t는 1을 가리키는 중
L.push_front(10); // 10 1 2
cout << *t << '\n'; // t가 가리키는 값 = 1을 출력
L.push_back(5); // 10 1 2 5
L.insert(t, 6); // t가 가리키는 곳 앞에 6을 삽입, 10 6 1 2 5
t++; // t를 1칸 앞으로 전진, 현재 t가 가리키는 값은 2
t = L.erase(t); // t가 가리키는 값을 제거, 그 다음 원소인 5의 위치를 반환
// 10 6 1 5, t가 가리키는 값은 5
cout << *t << '\n'; // 5
for(auto i : L) cout << i << ' ';
cout << '\n';
for(list<int>::iterator it = L.begin(); it != L.end(); it++)
cout << *it << ' ';
- push_back, pop_back, push_front, pop_front는 모두 O(1)
면접 시에 물어볼 수 있는 문제들
1. 원형 연결 리스트 내의 임의의 노드 하나가 주어졌을 때 해당 List의 길이를 효율적으로 구하는 방법?
☑️시간복잡도와 공간복잡도를 생각하라!
[정답] 동일한 노드가 나올 때까지 계속 다음 노드로 가면 됨 -> 공간복잡도 O(1), 시간복잡도 O(N)
2. 중간에 만나는 두 연결 리스트의 시작점들이 주어졌을 때 만나는 지점을 구하는 방법?
[정답] 일단 두 시작점 각각에 대해 끝까지 진행시켜서 각각의 길이를 구함. 그 후 다시 두 시작점으로 돌아와서 더 긴 쪽을 둘의 차이만큼 앞으로 먼저 이동시켜놓고 두 시작점이 만날 때까지 두 시작점을 동시에 한 칸씩 전진시키면 됨 -> 공간복잡도 O(1), 시간복잡도 O(A+B)
3. 주어진 연결 리스트 안에 사이클이 있는지 판단하라
[정답] Floyd's cycle-finding algorithm: 한 칸씩 가는 커서와 두 칸씩 가는 커서를 동일한 시작점에서 출발시키면 사이클이 있을 경우 두 커서는 반드시 만나게 됨 -> 공간복잡도 O(1), 시간복잡도 O(N)
