[논문] Consistent Autoformalization for Constructing Mathematical Libraries

수학적 표현을 자동화된 방식으로 형식화하는 과정에 대한 연구를 다룬다. 이 연구의 주된 목표는 비공식적인 수학적 증명을 형식적 증명으로 변환하는 autoformalization 방법을 개발하는 것이다. 이를 통해 수학적 지식을 자동으로 증명 시스템에 통합할 수 있는 라이브러리를 구축할 수 있다. 이 과정은 주로 Isabelle과 같은 수학적 증명을 다루는 증명 시스템에 사용될 수 있다.

Framework 알고리즘

• 1단계: round for retrieval augmented autoformalization로 구성된 한 라운드를 포함
• 2단계: 노이즈 제거(round for denoising)를 위한 한 라운드를 포함
• 3단계: 구문 오류를 바탕으로 코드를 개선하는 여러 반복적인 라운드로 구성.

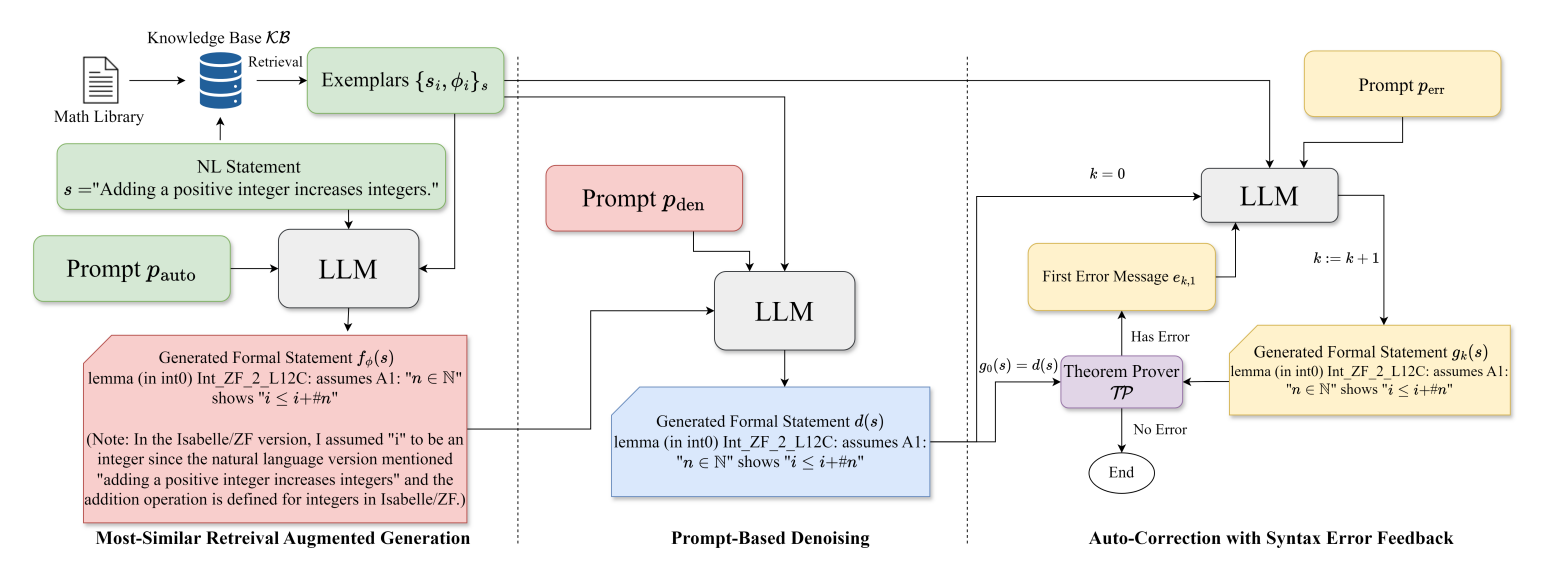
핵심 아이디어

1. autoformalization: autoformalization는 수학적 증명을 기계적으로 변환하여 공식적인 증명 시스템에서 사용할 수 있는 형식으로 만드는 작업이다. 이 연구에서는 LLM을 사용하여 이 작업을 자동화하고 있다. 구체적으로, 비공식적인 수학적 진술(예: 자연어로 작성된 수학 문제나 정리)을 Isabelle/ZF와 같은 형식 언어로 변환하는 방법을 제시한다.

2. Semantic correctness: 변환된 형식 명제가 해당 모델에서 정확히 해석될 수 있음을 의미합니다. 라이브러리 기반 자동 형식화는 이미 형식화된 수학적 명제들이 포함된 지식베이스(KB)를 활용하여, 새로 생성된 명제가 KB의 명제들과 의미적으로 일관되도록 한다.

3. 유사한 검색 증강 생성 (MS-RAG): 자동 형식화를 위해 LLM을 사용할 때, 기존의 예시 세트 { (si, ϕi) }를 기반으로 변환 함수가 정의됩니다. 하지만 고정된 예시는 각 하위 분야에서 새로운 정의나 개념의 사용을 반영하지 못하므로, KB에서 유사성을 기반으로 샘플을 검색하여 더 나은 변환 결과를 도출하는 방법을 제안합니다.

4. 노이즈 제거: LLM이 자동 형식화를 수행할 때, 훈련 데이터에서 비롯된 편향으로 인해 불필요한 텍스트나 중복된 내용이 생성될 수 있습니다. 이를 해결하기 위해 코드 기반 노이즈 제거(CBD)와 프롬프트 기반 노이즈 제거(PBD) 방법을 제안합니다. 이 방법들은 불필요한 설명이나 증명을 제거하고, 의미적 일관성을 유지하며 형식화를 개선합니다.

5. 구문 오류 피드백을 통한 자동 수정 (Auto-SEF): 형식화된 코드의 유효성은 정리된 정리 증명 시스템을 사용하여 확인할 수 있습니다. 만약 유효하지 않다면, 구문 오류가 출력되고, 이를 피드백으로 사용하여 자동으로 수정할 수 있습니다. 이 방법은 LLM이 형식화 오류를 자동으로 수정하는 과정입니다. 구체적으로는 오류를 수정하기 위한 프롬프트를 추가하고, 오류 피드백을 사용하여 자동 수정 과정을 반복적으로 진행합니다.

6. 성능 측정 지표: autoformalization의 성능을 평가하기 위해 여러 가지 지표가 사용된다. 이 논문에서는 BLEU, ChrF, RUBY, CodeBERTScore 등 다양한 지표를 통해 autoformalization된 증명과 기존 정리 간의 의미적 유사성을 측정하고 있다.

   • BLEU와 ChrF는 주로 기계 번역에서 사용되는 지표로, 단어 수준과 문자 수준에서의 유사성 측정
   • RUBY는 코드 생성 작업에 특화된 지표로, 생성된 코드와 기준 코드 간의 유사성 계산
   • CodeBERTScore는 코드 생성 성능을 평가하기 위한 모델 기반 지표로, 코드의 토큰 수준 표현을 사용해 평가

기여 및 응용

이 연구는 수학적 문제 해결에서 자동화된 접근을 제공하며, 특히 형식화된 수학적 정의와 정리를 증명 시스템에 통합하려는 시도에서 중요한 기여를 합니다. 이를 통해 수학적 지식을 효율적으로 처리하고, 수학적 증명과 관련된 자동화된 작업을 가능하게 합니다. 또한, 이 방법은 수학적 라이브러리를 구축하는 데 유용하게 적용될 수 있습니다.

논문에서는 이 방법을 실험적으로 평가하고, 다양한 지표를 통해 모델의 성능을 비교하여, 자동 형식화 기술이 실제로 수학적 증명 시스템에서 어떻게 활용될 수 있는지를 보여준다.

결말

이 연구는 수학적 문제 해결에서 자동 형식화를 통해 수학적 정의와 정리를 증명 시스템에 효율적으로 통합하는 기술을 제공한다. 이를 통해 수학적 지식 처리와 증명 자동화를 가능하게 하며, 수학 라이브러리 구축에도 응용될 수 있다. 다양한 지표를 통해 모델 성능을 평가하며, 자동 형식화 기술의 실제 활용 가능성을 입증한다.