해시 충돌

해시 충돌이란?

해시 함수가 서로 다른 입력 데이터에 대해 같은 출력값을 반환하는 경우 해시 충돌이 발생합니다.

먼저 해시맵에 대해서는 해시맵글로 대체하겠습니다:)

해시 충돌이 발생할 경우 2가지 방법으로 해결할 수 있습니다.

1. 개별 체이닝(Separate Chaning)방식

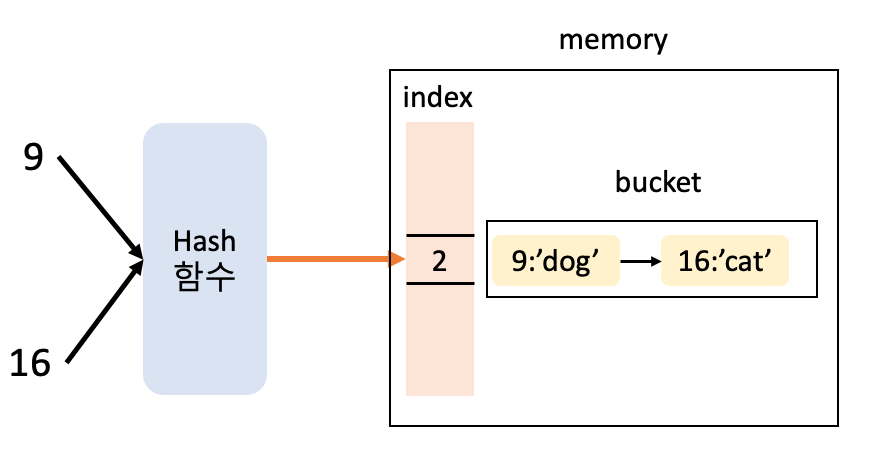
충돌이 발생할 경우 해당 버킷에 연결리스트를 이용해 데이터를 모두 저장하는 방식 입니다.
예를 들어 아래의 경우,,
$hash(x)=x\%7$일 경우, 9와 16의 해시 값은 동일하게 됩니다.
따라서, 개별 체이닝 방식을 이용하면, 해당 인덱스의 값을 저장하는 버킷에 연결 리스트 방식으로 모든 데이터를 저장하게 됩니다.

2. 개방 주소법(Open Addressing)

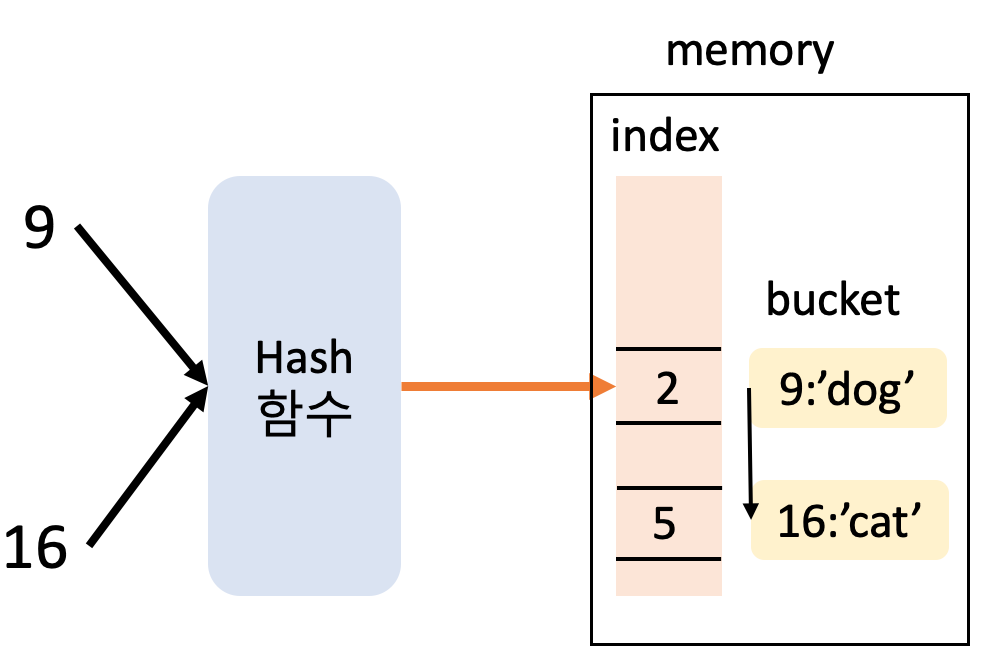
충돌이 발생할 경우 다른 해시 값을 사용해 데이터에 저장하는 방식입니다.
다른 해시값을 고르는 방법에는 선형 탐사, 제곱 탐사, 이중 해싱 등 여러 방법이 있습니다.
위에서와 같이 $hash(x)=x\%7$일때 9와 16이 같은 해시 값을 가질 경우 먼저 입력된 9의 값은 인덱스 2의 버킷에 저장되지만, 16의 값은 인덱스 2 근처에 비어있는 메모리 공간에 저장됩니다.

데이터 저장 규칙

개방 주소법을 이용할 때 빈 공간을 찾는 것에도 규칙이 있습니다.

1. 선형 탐사(Linear Probing)
   선형 탐사 방법은 충돌이 발생한 버킷에서 일정한 간격으로 다른 버킷을 찾아 데이터를 삽입하는 방법입니다.
   ex) i+1, i+2, i+3 ...
2. 제곱 탐사(Quadratic Probing)
   제곱 탐사 방법은 충돌이 발생한 버킷에서 간격을 제곱한 값만큼 더해서 다음 버킷을 찾아 데이터를 삽입하는 방법입니다.
   ex) i+1^2, i+2^2, i+3^2 ...
3. 이중 해싱(Double Hashing)
   이중 해싱 방법은 충돌이 발생한 버킷에서 해시 함수를 또 다른 해시 함수로 사용하여 일정 간격으로 다른 버킷을 찾는 방법입니다.

시간 복잡도

해시 알고리즘의 평균적인 시간 복잡도는 O(1) 입니다.
하지만, 모든 입력 값이 같은 해시 값을 가지는 최악의 경우 시간 복잡도는
O(N)이 됩니다.

해시 테이블의 이용

해시 테이블은 일반적으로 시간복잡도가 O(1)이기 때문에, 반복적인 계산을 할때 이전에 계산된 값을 미리 저장해 두고 필요할때 꺼내오면 시간을 많이 단축 할 수 있습니다.
그 예시로 피보나치 함수가 있습니다.
피보나치 함수는 동적 계획법을 이용해 풀 수 있는 대표적인 문제로, 큰 문제를 작은 여러 문제들로 나누어 독립적으로 해결해 나가는 방식입니다.
여기에서 작은 여러 문제들 중 중복되는 문제들이 많기 때문에, 중복되는 문제를 푸는데 시간을 절약하기 위해 해시 테이블을 이용합니다.

• 해시 테이블을 이용하지 않은 경우

	def fibonacci(n):
    if n == 0 or n == 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

• 해시 테이블을 이용한 경우

# 해시 함수 구현
def hash_function(key, size):
    return key % size

# 해시 테이블 정의
hash_table = {}

# 피보나치 수열 계산 함수
def fibonacci(n):
    # 해시 테이블에 저장된 값이 있다면 바로 반환
    if hash_table.get(n):
        return hash_table.get(n)
    
    if n <= 1:
        return n
    
    # 해시 테이블에 저장된 값이 없다면 계산 후 저장
    result = fibonacci(n-1) + fibonacci(n-2)
    hash_table[n] = result
    
    return result

두 함수의 결과 비교

입력값 n	사용 X	사용 O
30	0.5242	0.00002s
40	...	0.00002s

숫자가 커질 수록 해시테이블 사용 유무의 시간 차도 커집니다.
40은 돌리다 포기