DFS/BFS 개념 정리
1. 그래프 탐색 알고리즘
그래프
여러 개체들이 연결되어 있는 자료구조
탐색
특정 개체를 찾기 위한 알고리즘
대표적인 문제 유형
-
경로탐색 유형 (최단거리, 시간)
a~b지점까지 가는데 최소 거리/최단 시간 구하기 -
네트워크 유형 (연결)
여러 개체들이 주어진 상태에서 연결되어 있는 그룹의 개수를 구하거나 두 개체가 같은 네트워크 안에서 연결되어 있는지 확인하기 -
조합 유형 (모든 조합 만들기)
여러가지의 조합을 모두 만들고 비교하기
2. DFS/BFS란?
DFS : 드라마 하나를 끝까지 보고 다른 드라마를 본다.
BFS : 여러 개의 드라마를 한편씩 본다.
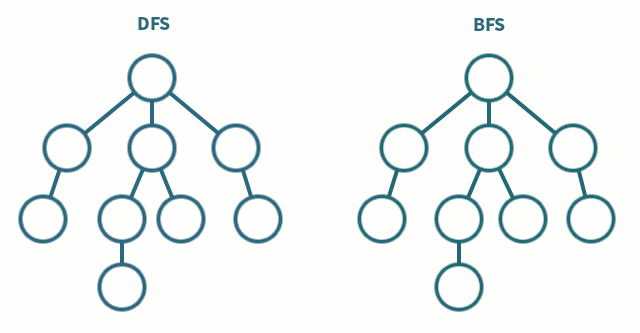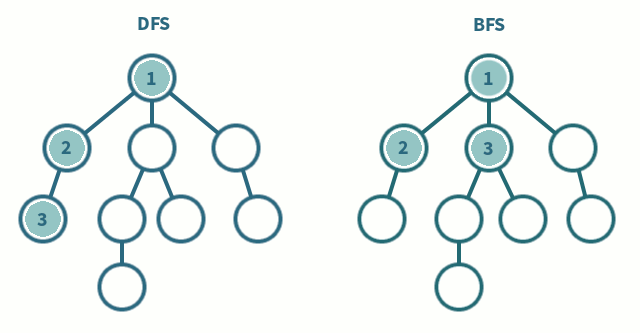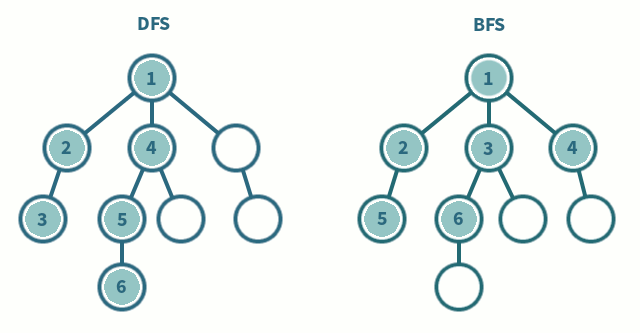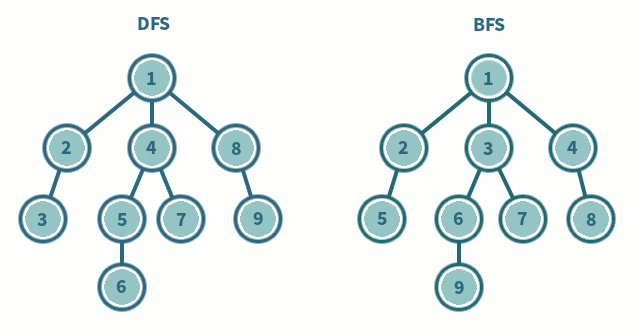
DFS (Depth First Search : 깊이 우선 탐색)
루트노드에서 시작해 다음 분기로 넘어가기 전 해당 분기를 완벽하게 탐색하는 방식으로 스택 또는 재귀함수로 구현한다.
-
장점
최단 경로를 빠르게 찾을 수 있다. -
단점
경로가 매우 길 경우, 탐색할 가지 수가 급격히 증가함에 따라 많은 기억 공간이 필요하다.
경로가 존재하지 않는 비연결 그래프일 경우, 모든 그래프를 탐색한 후 실패로 끝난다.
BFS (Breadth First Search : 넓이 우선 탐색)
루트노드에서 시작해 인접한 노드를 먼저 탐색하는 방식으로 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법이다. 큐를 이용해서 구현한다.
-
장점
현 경로상의 노드를 기억하기 때문에 적은 메모리를 사용한다.
찾으려는 노드가 깊은 단계에 있는 경우, BFS보다 빠르다. -
단점
경로가 존재하지 않아도 끝날 때까지 탐색한다.
최단 경로를 찾을 수 없다.
DFS vs BFS
- 모든 노드를 방문하고자 하는 경우에는 DFS를 가까운 노드부터 탐색하기 위해서는 BFS를 사용한다.
- 검색 속도 자체는 BFS가 빠르지만 DFS가 더 간단하다.
- 검색 대상 그래프가 크거나 경로의 특징을 저장해둬야 하는 문제는 DFS를,
검색 대상의 규모가 크지 않고 최단거리를 구해야 하는 문제는 BFS가 유리하다.
3. DFS/BFS 구현
DFS
- 정점을 방문한다
- [1]의 정점으로부터 인접한 정점 중 아직 방문하지 않은 정점이 없다면 탐색을 종료하고 가장 마지막으로 방문했던 정점으로 돌아가서 DFS를 진행한다
- [1]의 정접으로부터 인접한 정점 중 아직 방문하지 않은 정점이 있다면 그 정점을 방문하고 해당 정점으로부터 다시 DFS를 진행한다.
C++
const int MAX = 100001;
// 방문 배열. visited[node] = true이면 node는 방문이 끝난 상태이다.
bool visited[MAX];
// graph는 인접 리스트, current는 현재 노드
void dfs(const vector<int> graph[], int current) {
visited[current] = true; // current 방문
// current의 인접 노드를 확인한다. 이 노드를 next라고 하자.
for(int next: graph[current]) {
// 만일 next에 방문하지 않았다면 next 방문
if(!visited[next]) {
dfs(graph, next);
}
}
}C#
using System;
public class Solution
{
int MAX = 100001;
// 방문 배열: true이면 해당 노드는 이미 방문을 한 상태
bool[] visited = new bool[MAX];
// graph는 인접 리스트, current는 현재 노드
void DFS(List<int[]> graph, int current)
{
visited[current] = true;
foreach (int next in graph[current])
{
if (visited[current] == false)
{
DFS(graph, next);
}
}
}
}BFS
- 루트에서 시작한다.
- 자식 노드들을 [1]에 저장한다.
- [1]에 저장된 노드들을 차례로 방문한다. 또한 각각의 자식들을 [2]에 저장한다.
- [2]에 저장된 노드들을 차례로 방문한다. 또한 각각의 자식들을 [3]에 저장한다.
- 위의 과정을 반복한다.
- 모든 노드를 방문하면 탐색을 마친다.
C++
const int MAX = 100001;
queue<int> q;
// 방문 배열. visited[node] = true이면 node는 방문이 끝난 상태이다.
bool visited[MAX];
// graph는 인접 리스트, source는 시작 노드
void bfs(const vector<int> graph[], int source) {
// source 방문한다.
q.push(source);
visited[source] = true;
// 큐가 빌 때까지 반복한다.
while(!q.empty()) {
// 큐에서 노드를 하나 빼 온다. 이 노드를 current라고 하자.
int current = q.front();
q.pop();
// current의 인접 노드들을 확인한다. 이 각각의 노드를 next라고 한다.
for(int next: graph[current]) {
// 만일 next에 방문하지 않았다면 next 방문한다.
if(!visited[next]) {
q.push(next);
visited[next] = true;
}
}
}
}C#
using System;
public class Solution
{
int MAX = 100001;
queue<int> q;
bool[] visited = new bool[MAX];
// graph는 인접 리스트, source는 시작 노드
void bfs(List<int[]> graph, int source)
{
// source 방문한다.
q.push(source);
visited[source] = true;
// 큐가 빌 때까지 반복한다.
while (!q.empty())
{
// 큐에서 노드를 하나 빼 온다. 이 노드를 current라고 하자.
int current = q.front();
q.pop();
// current의 인접 노드들을 확인한다. 이 각각의 노드를 next라고 한다.
foreach (int next in graph[current])
{
// 만일 next에 방문하지 않았다면 next 방문한다.
if (!visited[next])
{
q.push(next);
visited[next] = true;
}
}
}
}
}
