이번에 풀어본 문제는
백준 13301번 타일 장식물 입니다.

📕 문제 링크

❗️코드

import java.io.BufferedReader
import java.io.InputStreamReader
import kotlin.system.exitProcess

fun main() {
    val br = BufferedReader(InputStreamReader(System.`in`))
    val N = br.readLine().toInt()

    if (N == 1) {
        print(4)
        exitProcess(0)
    }

    val sides: Array<Long> = Array(N + 1) { 0 }
    val perimeters: Array<Long> = Array(N + 1) { 0 }

    sides[1] = 1
    sides[2] = 1

    perimeters[1] = 4
    perimeters[2] = 6

    for (i in 3 .. N) {
        sides[i] = sides[i - 2].plus(sides[i - 1])
        perimeters[i] = perimeters[i - 1].plus(sides[i].times(2))
    }

    print(perimeters[N])
}

📝 풀이

sides 배열에는 N에 따른 추가될 변의 크기를 담고, perimeters 배열에는 둘레를 담습니다.
변의 크기는 이전 두개의 값을 더하면 구할 수 있고,
둘레의 합은 이전 둘레 + (추가될 변의 크기 * 2)
를 해주시면 됩니다.
그림을 그려보시면 쉽게 이해하실 수 있는데,

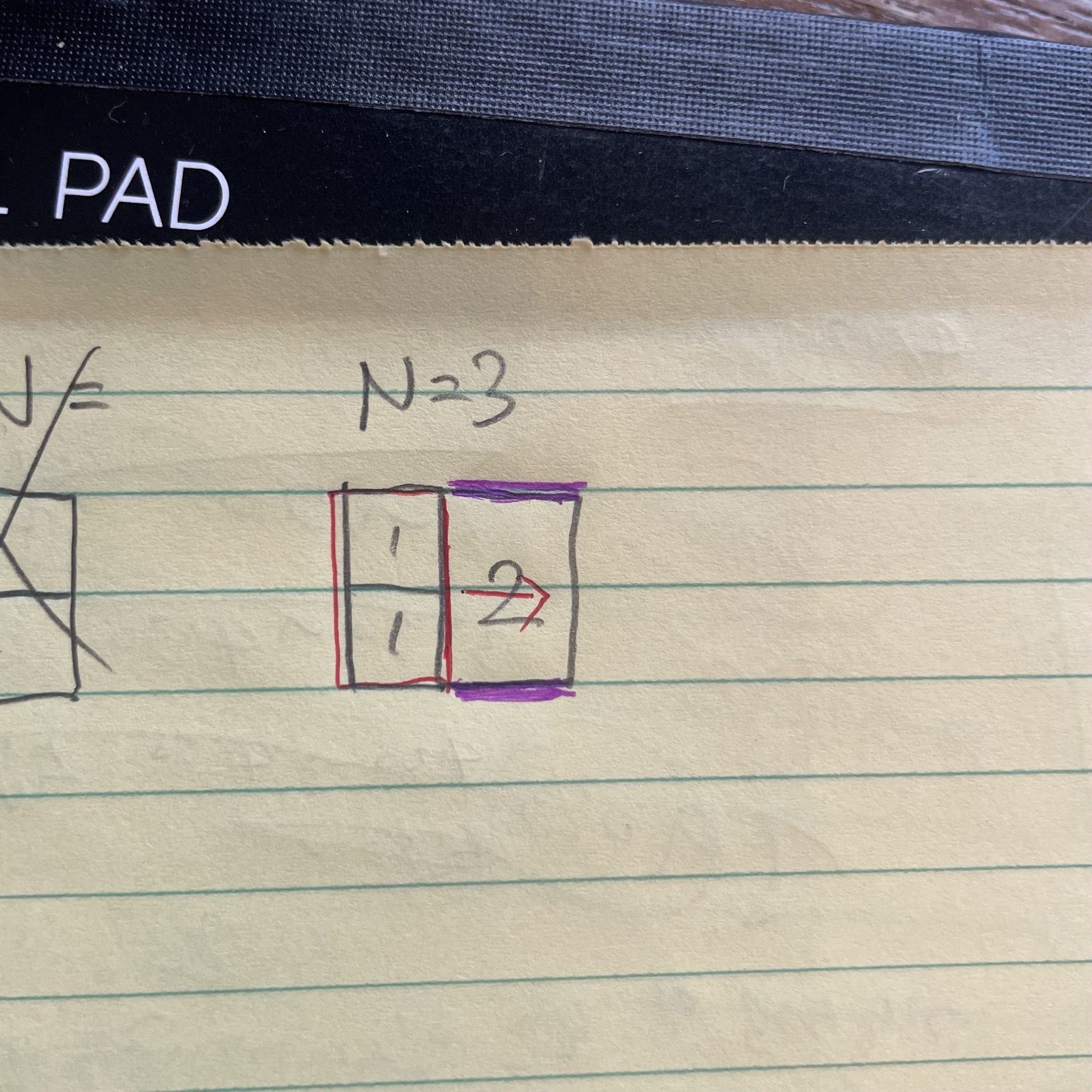
3 번째 정사각형(2)가 추가되는 상황이라 했을 때,
이전 둘레는 빨간색, 추가될 변들은 보라색으로 칠해보았습니다.

위 그림을 보면, 새로운 정사각형이 추가되면서 겹쳐져 제외되는 한 변이 그대로 옆으로 옮겨진다고 생각하시면, 이전 둘레에서 새로운 정사각형 2개의 변의 크기만 더해주면 다음 둘레를 구할 수 있습니다.

위 규칙을 토대로 N번 반복하고 perimeters 배열의 마지막 인덱스 N의 값을 출력하면 해결할 수 있습니다.