역전파 알고리즘

꼬부썬·2022년 8월 2일

역전파 : 다층 퍼셉트론 학습에 사용되는 통계적 기법

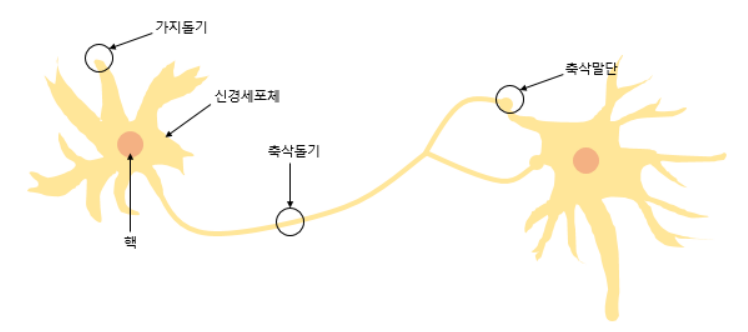
뉴런의 그림

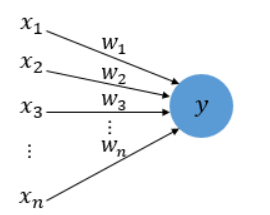
퍼셉트론의 그림

뉴런에서의 입력신호(받아들이는 반응) = 입력값

뉴런에서의 출력신호 = 출력값

퍼셉트론 그림에서 x는 입력값, w는 가중치, y는 출력값, 원은 인공뉴런.

즉, 퍼셉트론은 뉴런이 정보를 받아서 문제를 처리하는 원리를 따라한 인공 뉴런.

입력값과 출력값을 모두 알고 있다면 퍼셉트론이 제대로된 결과를 출력했는지 확인할 수 있지만 결과를 제대로 맞추지 못할 때에는 학습오류(training error)를 만들어낸다.

학습오류를 줄이기 위해서는 퍼셉트론의 성능 개선이 필요하고 이에 따라 가중치를 변경해야 한다. 최종적으로는 최적의 가중치 조합을 찾아서 학습오류를 줄이고 성능을 개선하여 문제 해결의 확률을 올리는 것이다.

퍼셉트론에서 가중치를 조정하는 방법은 퍼셉트론 알고리즘을 이해해야 한다.

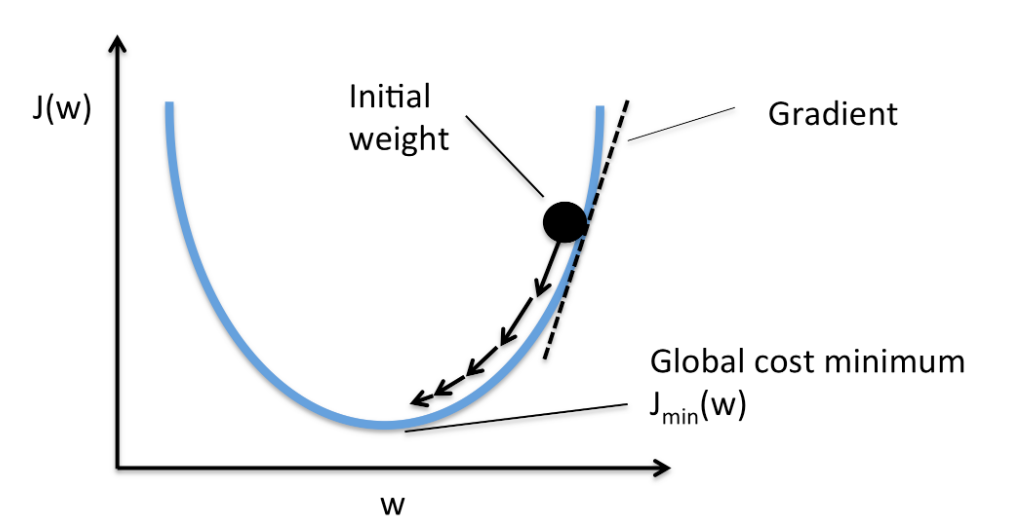
*위를 경사하강법 이라고 함(최적화 알고리즘 중 하나) 이것을 이용해서 오차가 더이상 줄지 않을 때까지 반복

퍼셉트론의 오류가 최소화되도록 가중치를 조정해 나간다. 여기에 정확도를 높이기 위해서는 편향(b값)을 포함해서 미세한 조정을 한다.

*편향(b)는 정확도를 높이고 얼마나 쉽게 활성화되는지 조절하는 변수이다.

풀어서 설명하자면, 생물의 뉴런의 경우 자극을 받았을 때 임계치가 어떤 한계를 넘어야만 자극이 다른 뉴런으로 전달된다. 이 때 편향이 높은 값이라면 적은 자극에도 쉽게 자극이 전달되는 것처럼 편향값에 따라 활성화정도를 조절할 수 있다.

퍼셉트론이 여러 입력을 받아들이면 여기에 가중치를 곱하고 편향을 합친 값이 활성화 함수(Activation function)을 지나 출력 여부를 결정한다. 이 때 출력 여부를 결정하는 거니까 값은 0, 1 둘 중 하나다.

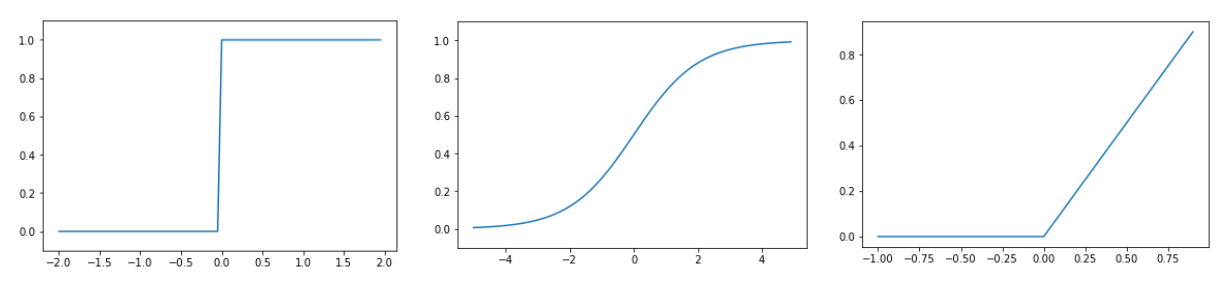
각각 스탭함수, 시그모이드 함수, 렐루(ReLU)함수이며, y값(출력값)이 모두 0 아니면 1이다.

위처럼 여러 입력값을 넣었을 때 하나의 결과값(y)만 출력하는 것을 단층 퍼셉트론이라고 하고, 단층 퍼셉트론에서는 활성함수가 1개밖에 없다.(아래 사진처럼)

*활성함수는 시그모이드 함수로 한다.(미분하기 용이해서 대표적으로 쓰임)

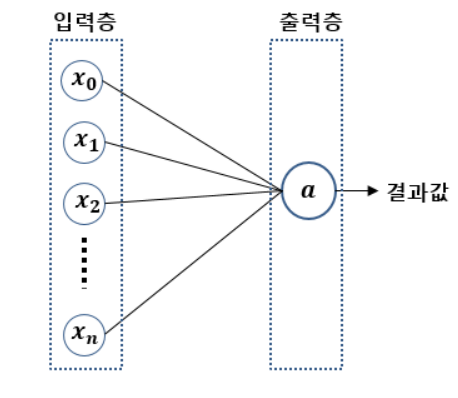
그러나 단층 퍼셉트론은 비선형적으로 분리되는 데이터에서는 제대로된 학습이 불가능 하다는 점이다.

비선형적 데이터는 아래와 같다.

그래서 비선형적으로 분리되는 데이터에 대해서도 학습이 가능하도록 입력층과 출력측 사이에 중간층(은닉층)을 넣는다.

이렇게 입력층과 출력층 사이에 여러 개의 은닉층이 있는 인공신경망을 심층 신경망(deep neural network)라고 부르며, 이 심층 신경망을 학습하기 위해 고안된 특별한 알고리즘들을 딥러닝이라고 한다.

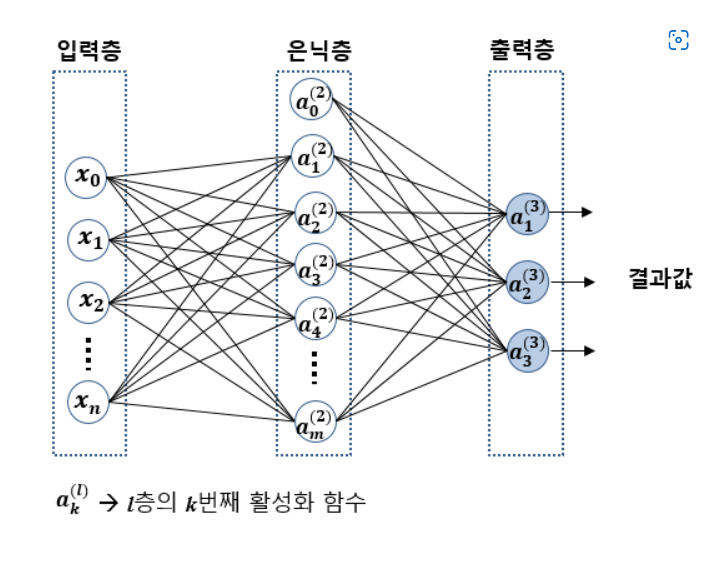
다층 퍼셉트론은 은닉층과 출력층에 존재하는 활성 함수와 이에 따른 가중치가 여러 개인 점 빼고는 단층 퍼셉트론과 동작 원리가 동일하다

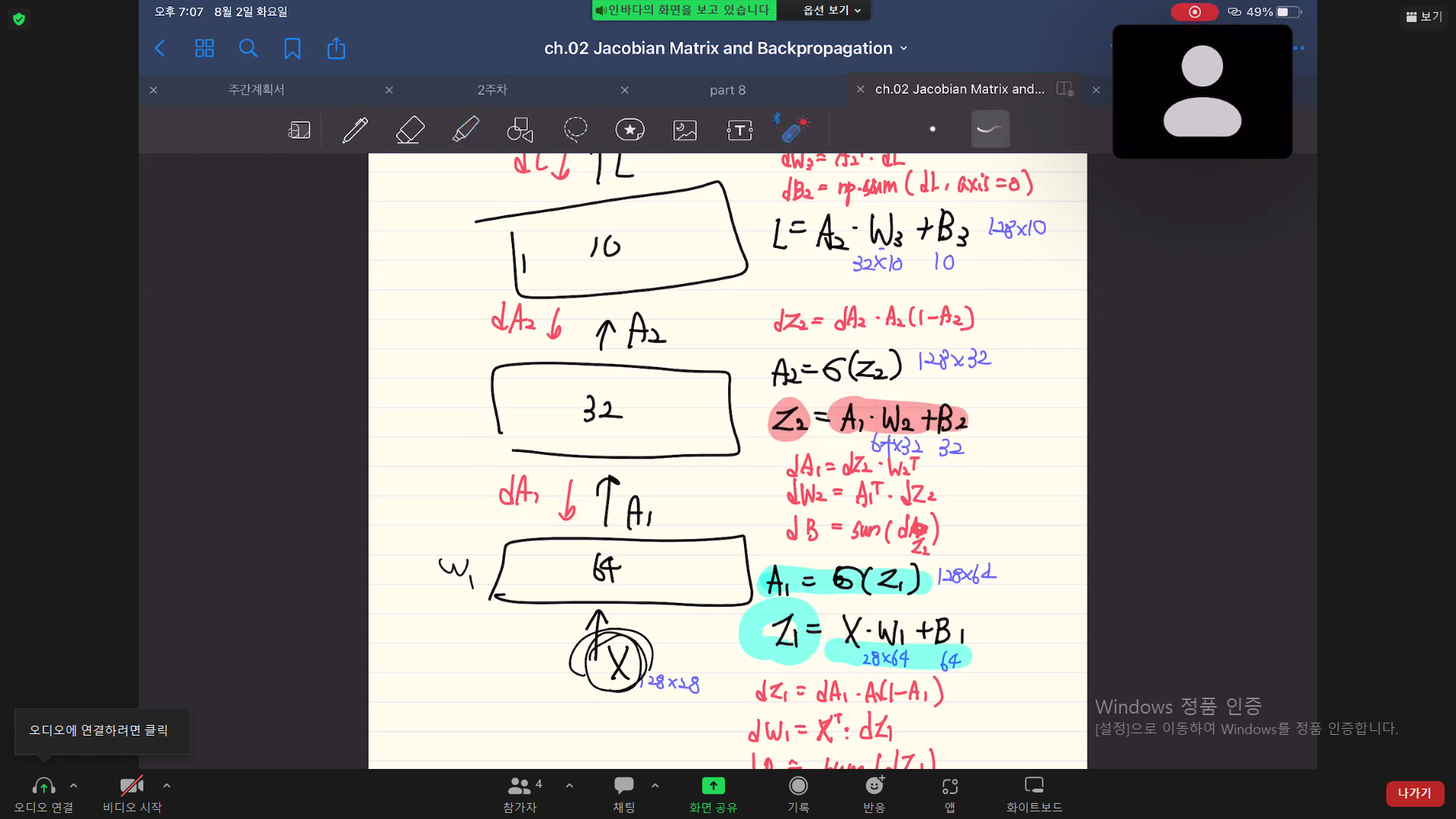
그러나 다층 퍼셉트론과 단층 퍼셉트론을 연결짓는 것이 어렵다. 그 이유는 단층 퍼셉트론에는 은닉층이 존재하지 않기 때문에 다층 퍼셉트론에서의 은닉층 출력값에 대한 기준값(위의 사진에서A1, A2)를 정의할 수 없기 때문이다.

이러한 문제를 해결하기 위해서 다층 퍼셉트론에서는 출력층에서 발생하는 오차값을 이용해서 은닉층으로 역전파(backpropagation)시켜 은닉층에서 발생하는 오차값에 따라 은닉층의 가중치를 업데이트한다.

역전파 = 은닉층의 가중치를 업데이트(학습)하기 위함이다. = 다층 퍼셉트론을 학습시키는 방법 = 다층 퍼셉트론에서의 최적화 과정

역전파의 방식

체인룰 : 합성 함수의 미분 원리