색상환

골드 3

해당 문제는 백준에서 Dynamic Programming을 사용해서 푸는 문제입니다.

이 문제를 정리하는 이유는 DP를 사용하기 위한 조건을 찾아내지 못하였기 때문입니다.

DP를 사용하기 위한 조건은 다음과 같습니다.

1. Overlapping Subproblems (겹치는 부분 문제)
2. Optimal Substructure (최적 부분 구조)

일단 문제부터 살펴봅시다.

문제

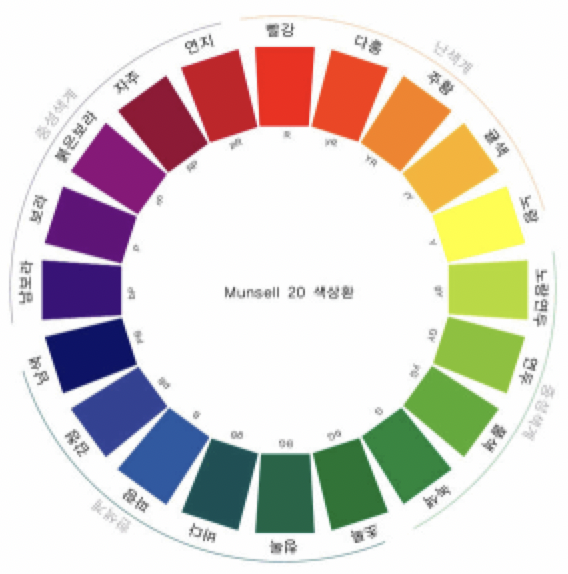
색을 표현하는 기본 요소를 이용하여 표시할 수 있는 모든 색 중에서 대표적인 색을 고리 모양으로 연결하여 나타낸 것을 색상환이라고 한다. 미국의 화가 먼셀(Munsell)이 교육용으로 고안한 20색상환이 널리 알려져 있다. 아래 그림은 먼셀의 20색상환을 보여준다.

색상환에서 인접한 두 색은 비슷하여 언뜻 보면 구별하기 어렵다. 위 그림의 20색상환에서 다홍은 빨강과 인접하고 또 주황과도 인접하다. 풀색은 연두, 녹색과 인접하다. 시각적 대비 효과를 얻기 위하여 인접한 두 색을 동시에 사용하지 않기로 한다.

주어진 색상환에서 시각적 대비 효과를 얻기 위하여 서로 이웃하지 않은 색들을 선택하는 경우의 수를 생각해 보자. 먼셀의 20색상환에서 시각적 대비 효과를 얻을 수 있게 10개의 색을 선택하는 경우의 수는 2이지만, 시각적 대비 효과를 얻을 수 있게 11개 이상의 색을 선택할 수 없으므로 이 경우의 수는 0이다.

주어진 정수 N과 K에 대하여, N개의 색으로 구성되어 있는 색상환 (N색상환)에서 어떤 인접한 두 색도 동시에 선택하지 않으면서 서로 다른 K개의 색을 선택하는 경우의 수를 구하는 프로그램을 작성하시오.

입력

입력 파일의 첫째 줄에 색상환에 포함된 색의 개수를 나타내는 양의 정수 N(4 ≤ N ≤ 1,000)이 주어지고, 둘째 줄에 N색상환에서 선택할 색의 개수 K(1 ≤ K ≤ N)가 주어진다.

출력

첫째 줄에 N색상환에서 어떤 인접한 두 색도 동시에 선택하지 않고 K개의 색을 고를 수 있는 경우의 수를 1,000,000,003 (10억 3) 으로 나눈 나머지를 출력한다.

예제 입력 1

4
2

예제 출력 1

2

풀이 접근 방식

먼저, 이 문제를 DP를 사용하기 위해서 반복되는 구조를 찾아야 합니다.

이 문제는 기본적으로 DP의 대표적인 문제 Knapsack과 유사하다고 생각되어 집니다.

다음을 봐봅시다.

색1	색2	색3	색4	...

여기서 생각해볼 수 있는 것은 색1을 칠했을 경우와, 칠하지 않았을 경우로 생각해볼 수 있습니다.

먼저, 색 1을 칠하는 경우는 다음과 같습니다.

색1	색2	색3	색4	...
O

이렇게 되었을 때 색2는 칠할 수 없습니다.

그렇다면 색3부터 색1을 칠할 경우와 동일하게 생각할 수 있습니다.

대신 칠해야 할 색은 1개 줄어들었을 것입니다.

다른 경우로 색1을 칠하지 않았을 경우를 확인해 봅시다.

색1	색2	색3	색4	...
X

이렇게 된다면 색2부터 새롭게 칠한다고 생각하면 됩니다.

이 경우에는 칠해야 할 색의 갯수는 줄지 않았습니다.

이것을 점화식으로 표현할 수 있습니다.

$DP[n][k] = DP[n - 2][k - 1] + DP[n - 1][k]$

여기서 DP의 경우 선형적으로 나열된 n개의 색상환 중에서 인접하지 않은 색 k를 결정하는 경우라고 생각할 수 있습니다.

⚡ 참고 ⚡

여기서, 헷갈릴 수 있는 부분이 있다.

"아니.. 위에서의 말대로라면 n번째 색상환에서만의 경우의 수가 아닌가?"라고 생각할 수 있습니다.

알고리즘 문제를 DP로 접근하는 경우 이와 같은 생각으로 접근하는 것이 아닙니다.

해당 방식은 이전에 구했던 값을 사용하는 Memoization 방식을 사용합니다.

Memoization 방식에서 중요한 것은 초기값을 어떻게 잡느냐에 따라 값이 크게 변동된다는 것입니다.

초기값을 요구하던 대로 잘 잡았다면, 올바른 점화식이라면 정상적으로 작동을 할 것입니다.

참고로 저의 생각을 정리한 것이라서 틀린 내용일 수 있기 때문에 만약 적절한 내용이 아니라면 댓글 남겨주시기 부탁드립니다.

이제 원형으로 구성되어 있는 색상환을 봐봅시다.

이때, 가장 문제는 1번째 색을 선택했다고 했을 경우 N번째 색을 선택할 수 없습니다.

그리고 1번째 색을 선택하지 않았다면, 선형적으로 구성되어 있을 때와 다를게 없습니다.

따라서, 1번째 색을 선택하는 경우에는 선택할 수 있는 색상에서 1번째 색, 2번째 색, N번째 색을 제외시켜줘야 합니다.

결국 구하고자 하던 DP[N][K] 값은 다음과 같습니다.

$DP[N][K] = DP[N - 3][K - 1] + DP[N - 1][K]$

코드

코드는 다음과 같습니다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
  static int MOD = 1000000003;
  public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

    int N = Integer.parseInt(br.readLine());
    int K = Integer.parseInt(br.readLine());

    if (N / 2 < K)  {
      System.out.println(0);
      return;
    }

    // 선형으로 된 N개의 색상환에서 K개를 선택하는 경우
    int[][] dp = new int[N + 1][K + 1];

    // 선형 DP 리스트 초기화
    init_dp(dp, N, K);

    // 선형 DP 리스트로 구하였기 때문에 원형의 상황을 가정해서 구해야 한다.
    System.out.println((dp[N - 3][K - 1] + dp[N - 1][K]) % MOD);


  }
  static void init_dp(int[][] dp, int N, int K) {
    for (int i = 1; i < N + 1; i++) {
      dp[i][0] = 1;
      dp[i][1] = i;
    }
    for (int i = 3; i < N + 1; i++) {
      for (int j = 2; j <= (i + 1) / 2 && j < K + 1; j++) {
        // 원형이 아닌 선형 DP 리스트이다.
        dp[i][j] = (dp[i - 1][j] + dp[i - 2][j - 1]) % MOD;
      }
    }
  }
}