Dynamic Programming

DP중에서도 대표적인 문제로 꼽히는 문제가 있는데, 타일 채우기, 계단 오르기, 배낭 채우기등이 있습니다.

그 중 하나인 배낭 채우기(Knapsack Problem)을 알아보겠습니다.

먼저 문제의 유형을 이해하기 위해서 예시를 통해서 살펴보겠습니다.

다음은 백준 12865번: 평범한 배낭 문제 입니다.

문제

이 문제는 아주 평범한 배낭에 관한 문제이다.

한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.

준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.

입력

첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.

입력으로 주어지는 모든 수는 정수이다.

출력

한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.

예제 입력 1

4 7
6 13
4 8
3 6
5 12

예제 출력 1

14

다음과 같이 문제가 주어집니다.

이 문제의 특징은 점화식에 접근할 때 잘못 접근하면 식을 세울 수가 없다는 것이 특징입니다.

대부분의 DP문제가 그러한 경우가 많지만, 이 문제는 특히 잘못 접근하면 잘못된 답을 도출해 냅니다.

이제 본격적으로 풀이 방법에 대해서 알아보자.

풀이 방법

당연하게도, 기본적인 방법으로도 풀 수 있긴 합니다.

1. 모든 경우의 수를 넣어봅니다. (Brute-Force)
2. 가격이 높은 보석, 혹은 (가격/무게) 의 값이 제일 높은 보석부터 먼저 골라서 넣는다. (Greedy)

1번의 경우 n개의 물건이 있다고 치면, n개 물건으로 만들 수 있는 가능한 부분집합(power set)의 수는 2^n개 입니다. 즉 시간 복잡도는 다음과 같습니다.

이 알고리즘은 너무 느립니다.

2번의 경우 그림을 통해서 확인해 볼 것입니다.

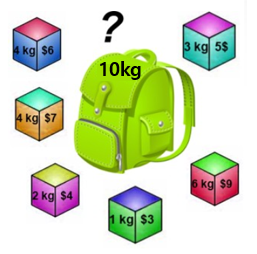
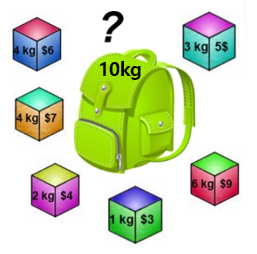
가격이 제일 높은 물건을 먼저 고르는 방법을 쓴다고 하면, 오른쪽 아래 있는 빠란 물건을 먼저 고르고 그 다음 왼쪾에 있는 노란 물건을 고를 것입니다. 그러면 10kg가 차고 가격의 합이 $16이 됩니다.

그렇지만 그림을 잘 보면서 다르 방법을 찾아보면, 왼쪽 물건 3개를 넣으면 10kg/$17이 된다는 것을 알 수 있고, 1/2/3/4kg짜리를 하나씩 넣으면 $19가 나옵니다. 즉, 이 방법은 최적의 답을 보장하지는 못합니다.

여기서 단순히 가격만 보지 말고, '무게당 가격'을 계산해서 제일 높은 것 부터 넣으면 되지 않을까라는 생각을 가질 수 있는데 이 방식은 항상 성립하지는 않습니다.

W = 30kg
물건 1: 5kg/$5 -- kg당 $1
물건 2: 10k/$6 -- kg당 $0.6
물건 3: 20kg/$14 -- kg당 $0.7

이 경우에 '무게당 가격'순으로 물건을 넣으면 물건 1, 물건 3이 들어가는데 가격의 합은 $19이고, 무게가 25kg으로 5kg이 남습니다.

보석 2와, 보석 3을 넣으면 30kg이 꽉차고 가격의 합이 $20입니다. 따라서 위의 방식이 '최적의 해'를 가져오지는 않는다는 것을 확인할 수 있습니다.

참고: Fractional Knapsack 문제는 Greedy로 풀 수 있습니다. 위 예시에서 물건 2를 반으로 잘라서 남은 5kg짜리 공간에 넣으면 그게 '최적의 해'입니다.

DP를 활용한 풀이 방식

이제 DP(Dynamic Programming)을 이용하여 문제를 풀어봅시다.

DP를 이용하기 위해선 두 가지 조건이 필요로 했습니다.

1. 중복되는 문제
2. 최적 부분 구조

여기서 먼저 어떤 부분이 중복되는지 확인해 봐야합니다.

집합 A를 n개의 물건들 중에 최적으로 고른 부분집합이라고 가정해봅시다.

• 집합 A가 n번째 물건을 포함하고 있지 않다면, A는 n번째 보석을 뺀 나머지 n - 1개 물건들 중에서 고른 부분집합과 같다.
• 집합 A가 n번째 보석을 포함하고 있다면, A에 속한 보석들의 총 가격은 n - 1개의 보석들 중에서 최적으로 고른 가격의 합에다가 보석 n의 가격을 더한 값과 같다. (단, n번째 보석을 넣었을 때 배낭이 터지지 않아야 합니다.)

지금까지 쓴 얘기를 점화식으로 풀어보면 다음과 같습니다.

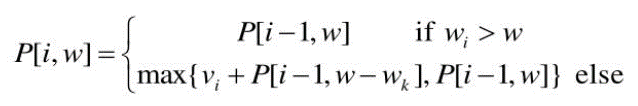
여기서 P[i, w]란 i개의 물건이 있고 배낭의 무게 한도가 w일 때 최적의 이익을 의미합니다.

식을 풀어보면 다음과 같습니다.

• i번째 물건이 배낭의 무게 한도보다 무거우면 넣을 수 없으므로 i - 1개의 물건들을 가지고 구한 전 단계의 최적값을 그대로 가져옵니다.
• 그렇지 않은 경우, i번째 물건을 위해 i번째 물건만큼의 무게를 비웠을 때의 최적값에 i번째 물건의 가격을 더한 값 vs i - 1개의 물건들을 가지고 구한 전 단계의 최적값 중 큰 것을 선택합니다.

많은 DP문제에서 2차원 배열을 자주 사용하는데 2차원 배열은 변수를 두 가지 이상을 활용할 수 있기 때문에 DP문제 풀이에 적합한 경우가 많습니다.

다음은 2차원 배열을 채워가는 과정을 사진으로 표현한 것들입니다.

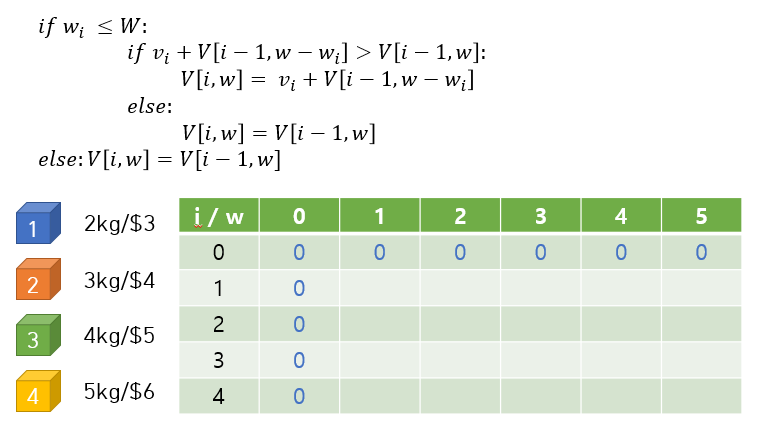
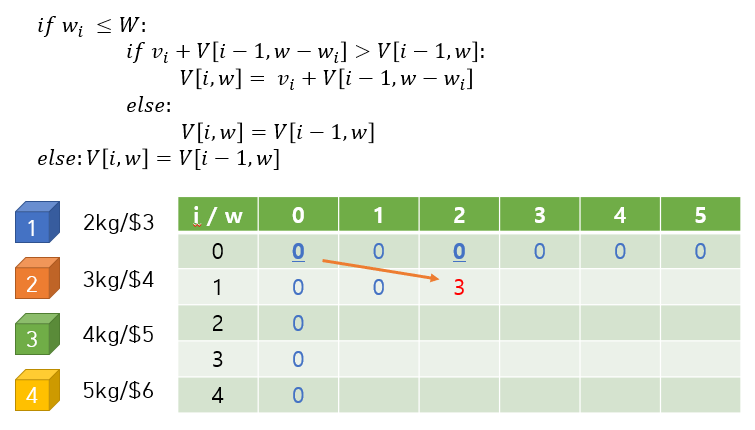
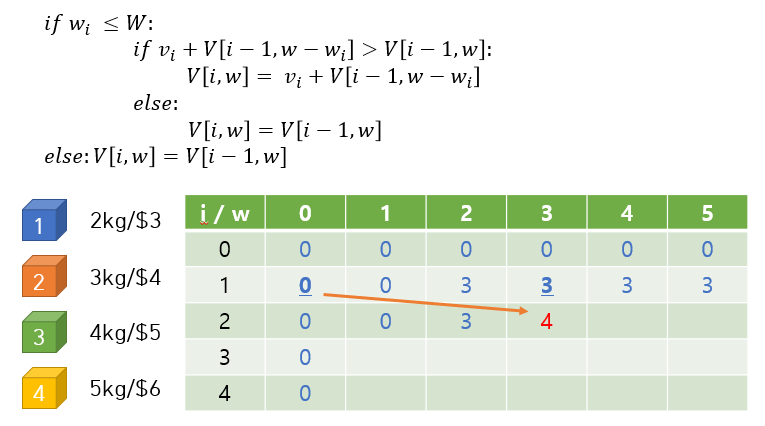
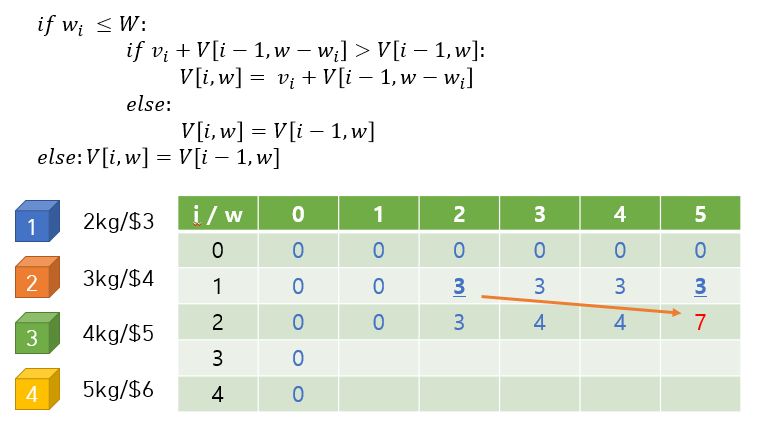
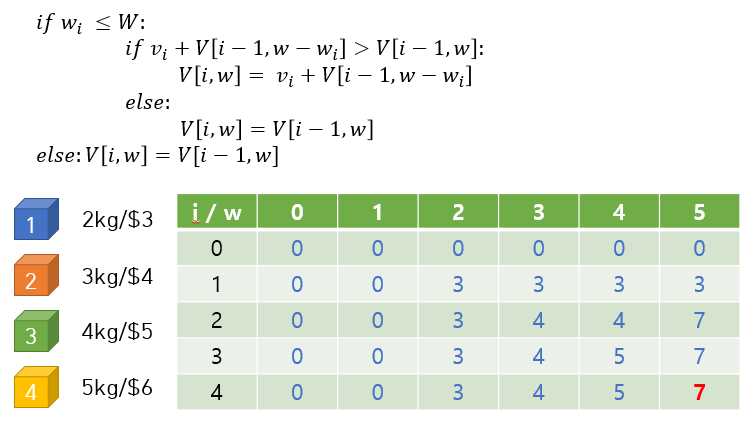
코드

Knapsack Problem의 코드는 다음과 같습니다.

static void knapsack_dp(int[][] knapsack, int[][] dp, int N, int K) {
  for (int i = 1; i < N + 1; i++) {
    for (int k = 1; k < K + 1; k++) {
      int itemWeight = knapsack[i][0];
      if (itemWeight > k)
        dp[i][k] = dp[i - 1][k];
      else {
        dp[i][k] = Math.max(dp[i - 1][k], knapsack[i][1] + dp[i - 1][k - itemWeight]);
      }
    }
  }
}