오늘은 저번 시간에 이어서 확률통계를 배우며 그래프를 그려보는 시간을 가지려고 합니다.
몸무게 리스트 만들기
input
import numpy as np
weight=[22,24,26,30,32,40,35,45,20,29,34,36,36,38,39,48,43,37,33,31,29,39,26,29]
hist=np.zeros(6) # 6개의 영배열
for i in weight:
if i//5==4: # // 정수몫, / 실수몫
hist[0]+=1
elif i//5==5:
hist[1]+=1
elif i//5==6:
hist[2]+=1
elif i//5==7:
hist[3]+=1
elif i//5==8:
hist[4]+=1
elif i//5==9:
hist[5]+=1
print(hist) output
[3. 5. 5. 7. 2. 2.]
zeros를 통해 값이 0인 배열을 6개 만들어 줍니다. append를 사용하여도 됩니다.
5키로 마다 통계표를 만들기 위해 5로 나눴을때 몫마다 각 인덱스에 더해줍니다.
input
import pandas as pd
index=['20~25','25~30','30~35','35~40','40~45','45~50']
#필드 1개만을 가지는 자료형
a=pd.Series(hist,index=index)
aoutput
20~25 3.0
25~30 5.0
30~35 5.0
35~40 7.0
40~45 2.0
45~50 2.0
dtype: float64
pandas의 Series함수는 직관적으로 이해하기 쉽게 엑셀 모형으로 출력값을 보여줍니다. 엑셀과 달리 시리즈는 행의 이름(index)과 열의 이름(name)을 원하는 대로 입력할 수 있습니다. 별도로 입력하지 않는다면 index는 0부터 시작하는 정수 값이, name은 빈 값(None)이 입력됩니다.
변수 이름 붙히기
input
#시리즈의 이름
a.name='A반의 체중 도수분포표'
a output
20~25 3.0
25~30 5.0
30~35 5.0
35~40 7.0
40~45 2.0
45~50 2.0
Name: A반의 체중 도수분포표, dtype: float64
name함수를 이용하여 변수에 이름을 붙혀줄 수 있습니다.
DataFrame을 이용하여 출력
input
height=[124,125,128,130,134,140,131,143,122,129,136,139,141,135,142,150,149,141,127,131,130,125,135,126]
d={'weight':weight, 'height':height}
#필드 2개 이상-데이터프레임
e=pd.DataFrame(d)
e.tail()output
DataFrame함수로 출력하게 되면 다음과 같이 정리되어 출력이 됩니다.
tail함수는 해당 변수에 들어가 있는 마지막 5개의 값을 출력하게 됩니다.
DataFrame을 이용하여 출력2
input
f=np.zeros((len(weight),2))
print(f.shape) #24행 2열의 2차원 배열
f[:,0]=weight # [행 , 열] [: , 0] 모든행, 0열
f[:,1]=height # 모든행, 1열
#데이터프레임에 필드명 지정
g=pd.DataFrame(f, columns=['weight','height'])
g.head() output
저는 이 방법으로 더 많이 출력하는 것 같습니다. 줄의 수는 더 늘어나지만 직관적으로 확인이 쉽습니다.
head함수는 tail과 반대로 처음 5개의 문항을 가져와줍니다.
그래프 출력 준비
input
import numpy as np
bins=np.arange(20,55,5) #20~54,5씩 증가
print(bins)
hist,b=np.histogram(weight,bins) #도수분포 계산 함수
print(hist) #빈도수
print(b) #구간output
[20 25 30 35 40 45 50][3 5 5 7 2 2]
[20 25 30 35 40 45 50]
그래프로 출력하여 확인 하기 위해 hist라는 이름으로 도수 분표 계산을 해줍니다.
그래프 출력
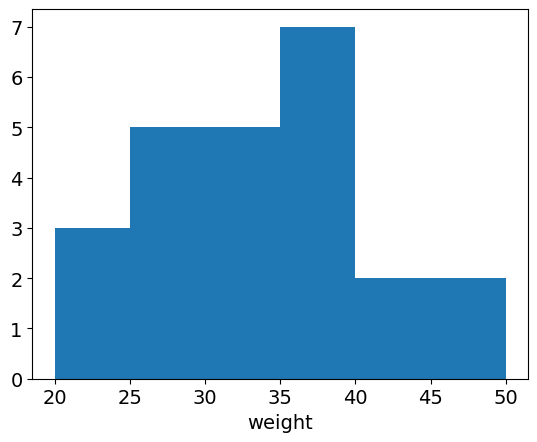
input
import matplotlib.pyplot as plt
plt.hist(weight,bins) #히스토그램 함수
plt.xlabel('weight',fontsize=14) #label 달기
plt.xticks(fontsize=14) # x축 내용 크기
plt.yticks(fontsize=14)
plt.show()output
plt.figure(figsize=(x값, y값))를 추가로 입력하게 되면 그래프의 크기 또한 조절 가능합니다.
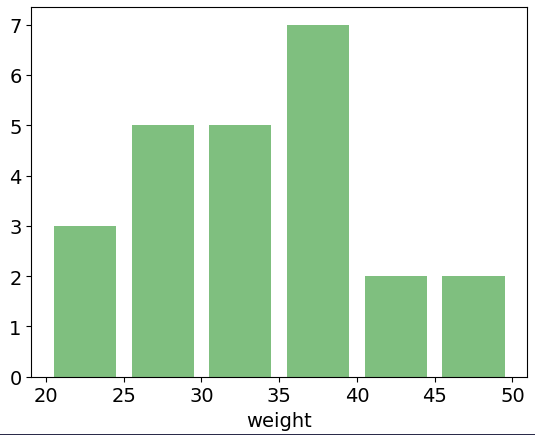
그래프 그리기 응용
input
import matplotlib.pyplot as plt
# rwidth 막대폭
plt.hist(weight,bins,rwidth=0.8,color='g',alpha=0.5)
plt.xlabel('weight',fontsize=14)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()output
그래프를 바꾸는 설정법은 여러가지 있으니 여러가지 이용하여 보기 쉽게 꾸며주시면 좋습니다.
평균값 구하기
input
x=[2,3,4,5,6,6,7,8,8,10]
def average(x):
return sum(x)/len(x) # 합계를 개수로 나누면 평균
print(average(x))
average2=lambda a : sum(a)/len(a)
print(average2(x))output
5.9
5.9
average와 average2는 직접 평균값을 구하는 함수를 만든 것입니다.
average함수
input
import numpy as np
x=[2,3,4,5,6,6,7,8,8,10]
print(np.average(x)) # 넘파이의 내장함수output
5.9
numpy 함수에 내장된 average 함수를 사용하여 간편하게 구할 수 있습니다.
중앙값구하기
input
x=[9,3,5,2,7,2,6,6,7,7,8,8,10]
x.sort() #오름차순 정렬output
[2, 2, 3, 5, 6, 6, 7, 7, 7, 8, 8, 9, 10]
matplotlib 모듈을 이용하여 그래프로 만들어 직관적으로 확인 하셔도 됩니다.
plt.hist(x)
plt.show()
를 사용하시면 됩니다.
중앙값구하기2
input
n=len(x) #자료수
middle_number=n//2 #중앙값(median)의 인덱스
print(middle_number)
print(x[middle_number]) #중앙값output
6
7
중앙값을 구할 때 x[변수]를 해주어야 합니다.
median함수
input
np.median(x) #넘파이의 내장함수output
7.0
빈도수 최대인덱스 구하기
input
#수치형 데이터 - 정규분포 => 평균, 비정규분포 => 중위수
#범주형 데이터 - 최빈수
bins=np.bincount(x) #도수분포
print(bins)
idx=bins.argmax() #최대값의 인덱스
print(x)
print(idx) output
[0 0 2 1 0 1 2 3 2 1 1][2, 2, 3, 5, 6, 6, 7, 7, 7, 8, 8, 9, 10]
7
bins = 각 데이터 빈도수이므로 x 값인 [2, 2, 3, 5, 6, 6, 7, 7, 7, 8, 8, 9, 10]에서 0과 1이 0개이기 때문에 0으로 출력되는 것을 확인 할 수 있습니다.
응용하기(var, std함수 구현)
input
import numpy as np
x=[0,1,3,6,12,13,10,7,5,1]
mean=np.average(x)
print(mean)
variance=0
for i in range(len(x)):
variance += (x[i]-mean)**2 # (변량-평균)의 제곱의 합
variance /= len(x) #자료수로 나누면 분산
std=np.sqrt(variance) #분산의 제곱근 : 표준편차
print(variance)
print(std)output
5.8
19.759999999999998
4.445222154178573
분산과 표준편차를 함수를 이용하여 구합니다.
응용2(var, std함수 활용)
input
mean=np.average(x)
print(mean)
print(np.var(x)) #분산
print(np.std(x)) #표준편차output
19.759999999999998
4.445222154178573
var과 std함수를 이용하여 구하는 방법입니다.
그래프 출력
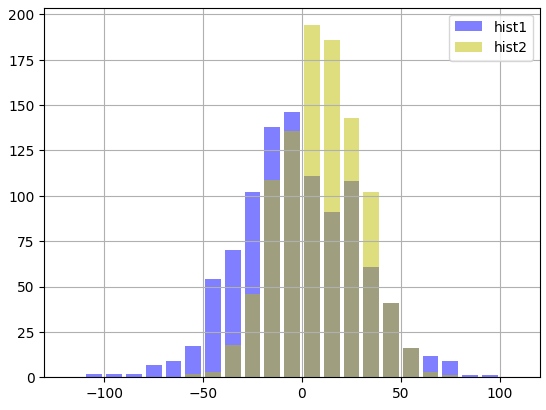
input
import matplotlib.pyplot as plt
bin=np.arange(-120,120,10)
print(bin)
# normal(평균,표준편차,샘플수) 정규분포 난수를 만드는 함수
#평균 hist1 < hist2 / 표준편차 hist1 > hist2
hist1=np.random.normal(0,30,1000)
#print(hist1)
hist2=np.random.normal(10,20,1000)
plt.hist(hist1,bin,alpha=0.5,rwidth=0.8,color='b',label='hist1')
plt.hist(hist2,bin,alpha=0.5,rwidth=0.8,color='y',label='hist2')
plt.legend()
plt.grid()output
평균과 표준 편차구하기
input
#평균 hist1 < hist2
print(np.mean(hist1))
print(np.mean(hist2))
#표준편차 hist1 > hist2
print(np.std(hist1))
print(np.std(hist2))output
-1.7935597332500754
9.720396222222243
29.817983553114754
20.065612778549905
오늘은 확률통계에 대해 공부해 보았습니다. 해당 내용이 많이 어렵지만 오히려 함수들의 의미만 알고 있다면 원하는 데이터를 쉽게 가져올 수 있기 때문에 매우 중요하다고 생각합니다 오늘도 긴글 보시느라 고생 많으셨습니다.