오늘은 분석 방법 중 로지스틱 회귀분석(logistic regression)에 대해 배워보도록 하겠습니다.

---

로지스틱 회귀분석(logistic regression)

로지스틱 회귀분석이란 이 전 시간에 배운 회귀분석에 대해 다시 한 번 기억해야합니다.
전 시간에 배운 선형 회귀분석은 단순/다중 모두 종속변수(Y)가 연속형이었습니다.
로지스틱 회귀분석은 독립변수(X)는 범주형 또는 연속형이며 종속변수(Y)가 범주형 이면서 0 또는 1인 경우 사용되는 회귀분석입니다.
특징으로는 두가지가 있습니다.

• 여러 설명 변수들로부터 두 범주만을 가지는 반응변수를 예측하는데 사용되며
• 분석결과 종속 변수 값, 즉 확률이 0.5보다 크면 사건이 일어난다고 판단, 0.5보다 작으면 그 사건이 일어나지 않는 것으로 예측합니다.

---

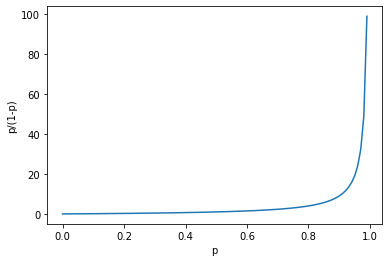
odds(오즈비)

input

import numpy as np 
import matplotlib.pyplot as plt 
np.random.seed(10) #랜덤시드 고정
probs=np.arange(0,1,0.01) # 0~1, 0.01 간격
# 오즈비 성공확률/실패확률
odds=[p/(1-p) for p in probs]
print(odds)
plt.plot(probs, odds)
plt.xlabel('p')
plt.ylabel('p/(1-p)')
plt.show()

output

[0.0, 0.010101010101010102, 0.020408163265306124, ..., 98.99999999999991]

odds는 실패에 비해 성공할 확률의 비를 나타내는 것입니다.

---

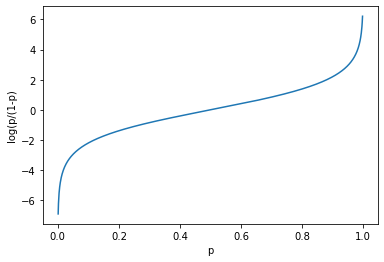
Logit(로직)함수

input

probs=np.arange(0.001, 0.999, 0.001)
# logit 함수 ( 오즈비에 로그 적용 )
logit=[np.log(p/(1-p)) for p in probs]
print(logit)
plt.plot(probs, logit)
plt.xlabel('p')
plt.ylabel('log(p/(1-p)')
plt.show()

output

[-6.906754778648554, -6.212606095751519, ..., 6.212606095751518]

odds에 log만 추가해 주면됩니다.

---

정리

input

zs=np.arange(-10, 10, 0.1)
# 위의 식을 z에 대해 정리한 식(logit 함수의 x,y축이 바뀜)
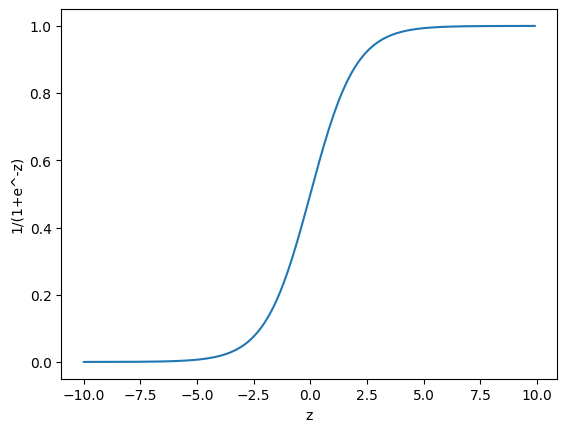
gs=[1/(1+np.exp(-z)) for z in zs]
print(gs)
plt.plot(zs, gs)
plt.xlabel('z')
plt.ylabel('1/(1+e^-z)')
plt.show()
#로지스틱 함수, 시그모이드 함수
# 출력값의 범위 0.0~1.0 

output

[4.5397868702434395e-05, 5.0172164683764205e-05, ..., 0.9999498278353162]

---

오늘은 로지스틱회귀분석의 기초에 대해 배워보았습니다.

😁 power through to the end 😁