경사하강법 - 3탄 (경사하강법 로직 및 분석)

jaybon·2022년 12월 3일

경사하강법

머신러닝 정리

목록 보기

9/9

개요

경사하강법 로직을 보면서 이해하고, 성능 및 효율을 비교해본다.

코드 설명 (배치 경사하강법)

배치 경사하강법 코드를 통해서 로직을 설명해본다.

주피터 노트북을 활용하였음.

전체코드

# 라이브러리 import
import numpy as np
import pandas as pd

# 배치 경사 하강법
def stochastic_gradient_descent(x : np.ndarray, y : np.ndarray, theta : np.ndarray, alpha : float, m, epoch : int, batchSize):
	# 특성을 pivot 한다. [[키, 몸무게], [키, 몸무게]] -> [[키, 키], [몸무게, 몸무게]]
    xTrans = x.transpose()
    # 에포크만큼 반복문을 돌린다. 
    for i in range(0, epoch):
    	# 가설을 세운다.
        hypothesis = np.dot(x, theta)
        # 가설과 라벨(실제 결과값)을 비교하여 손실을 구한다.
        loss = hypothesis - y
        # 비용을 구한다.
        cost = np.sum(loss ** 2) / (2 * m)
        # 경사를 구한다.
        gradient = alpha * np.dot(xTrans, loss) / m
        # 가중치를 업데이트한다.
        theta = theta - gradient
    # 결과를 리턴한다.
    return ("배치" , cost, theta)

# 데이터 로드
df = pd.read_csv('data/byong_data_set1.csv')

# 데이터 세팅
x = df[['height', 'weight']].values # 특성 (feature)
y = df[['bmi']].values # 라벨 (label)
m, n = np.shape(x) # m : 데이터 개수, n : 특성 개수
epoch = 5 # 에포크 (epoch)
theta = np.ones(n).reshape(-1, 1) # 임의 가중치
alpha = 0.00001 # 학습률
batchSize = 100 # 미니 배치 크기

# 경사하강법 실행
result = batch_gradient_descent(x, y, theta, alpha, m, epoch, batchSize)

0. 라이브러리 import

수학 계산 라이브러리 numpy
csv 등의 데이터를 가공할 수 있는 pandas

import numpy as np
import pandas as pd

1. 데이터 로드

예제로 병무청 신체검사 데이터를 사용하였다.

https://www.data.go.kr/data/3064321/openapi.do

pandas를 이용해서 csv 파일을 가져온다.

df = pd.read_csv('data/byong_data_set1.csv')
df.head()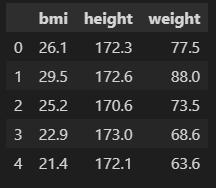

2. 데이터 세팅

2-1. 특성

pandas로 특성으로 이용할 수 있는 컬럼만 가져온다.

x = df[['height', 'weight']].values
x

array([[172.3,  77.5],
       [172.6,  88. ],
       [170.6,  73.5],
       ...,
       [177.5,  82.4],
       [191.6, 116.1],
       [171.4,  68. ]])

2-2. 라벨

라벨이란 특성을 이용하여 예측해야할 실제 결과값을 뜻한다.

y = df[['bmi']].values
y

array([[26.1],
       [29.5],
       [25.2],
       ...,
       [26.1],
       [31.6],
       [23.1]])

2-3. 샘플 개수와 특성 개수

numpy의 shape 메소드를 사용하여 샘플의 개수와 특성의 개수를 확인한다.

m = 계산할 샘플들의 개수
n = 계산할 특성 개수

m, n = np.shape(x)
print(m)
print(n)

217000
2

2-4. 에포크

에포크는 계산할 표본 집단의 샘플들을 모두 순회했을 때 1회 카운트 된다.

예시로 가져온 신체검사 데이터 217000개를 모두 계산하여야 1회 완료.

epoch = 5

2-4. 임의 가중치

키와 몸무게에 적용할 임의의 가중치를 설정한다.

$\hat{y} = 170 * a + 70 * b$ 일 때

실제 결과값 $y$ 에 근접하는 예측값 $\hat{y}$ 을 산출하는 a와 b를 구하도록 학습시킨다.

기본으로 1로 모두 세팅하였음.

theta = np.ones(n).reshape(-1, 1)
theta

array([[1.],
       [1.]])

2-5. 학습률

learning_rate 라고 하며, 계산을 러프하게 할 것인지 세밀하게 할 것인지 설정한다.

규제의 역할도 한다.

alpha = 0.00001

2-6. 배치 사이즈

한번 update 할 때 계산해야할 샘플의 수를 뜻한다.

배치 경사하강법의 배치사이즈 = 표본 집단 전체 샘플 수
확률적 경사하강법의 배치사이즈 = 1
미니 배치 경사하강법의 배치사이즈 = 보통 10 이상

batchSize = 100

3. 경사하강 함수

3-1. 특성 pivot

특성을 계산하기 편하도록 numpy의 transpose 메소드로 행과 열을 바꾸는 pivot을 실행한다.

array([[172.3,  77.5],
       [172.6,  88. ],
       [170.6,  73.5],
       ...,
       [177.5,  82.4],
       [191.6, 116.1],
       [171.4,  68. ]])

아래와 같이 바뀐다.

xTrans = x.transpose()
xTrans

array([[172.3, 172.6, 170.6, ..., 177.5, 191.6, 171.4],
       [ 77.5,  88. ,  73.5, ...,  82.4, 116.1,  68. ]])

3-2. 예측값 (가설)

가중치와 샘플을 계산하여 예측값을 내놓는다.

비교를 위해 y 값과 예측값을 확인해보자.

아래 y 값은 실제 bmi 결과값이다.

array([[26.1],
       [29.5],
       [25.2],
       ...,
       [26.1],
       [31.6],
       [23.1]])

아래 코드를 보자.

numpy의 dot 메소드는 행렬을 곱한다.

x와 theta는 형식이 다른데 numpy가 내적과 행렬곱을 알맞게 계산해준다.

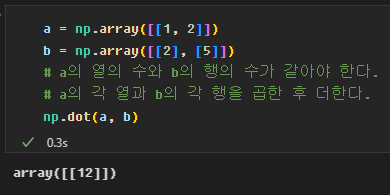
아래는 예측값이다.

처음에 임의로 가중치를 설정하였기 때문에 정확하지 않은 예측값을 보여준다.

가중치를 업데이트하여 결과값과 예측값의 차이를 줄여나가야 한다.

hypothesis = np.dot(x, theta)
hypothesis

array([[249.8],
       [260.6],
       [244.1],
       ...,
       [259.9],
       [307.7],
       [239.4]])

3-3. 손실 (잔차)

라벨(결과값)과 가설(예측값)을 비교하여 손실을 구한다.

보기에는 단순한 빼기이지만,

numpy를 사용하면 해당 행렬의 같은 열 끼리 계산이 된다.

loss = hypothesis - y
loss

array([[223.7],
       [231.1],
       [218.9],
       ...,
       [233.8],
       [276.1],
       [216.3]])

3-4. 비용

비용함수를 이용하여 비용을 구한다.

비용은 학습데이터에 존재하는 전체의 에러 정도를 의미하며, 낮아져야 한다.

가장 낮은 비용을 찾아내는 것이 경사하강법의 목표이다.

비용은 보통 아래의 방식으로 구한다.

MSE(Mean Squared Error, 평균 제곱 오차)

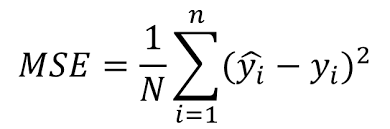
MAE(Mean Absolute Error, 평균 절대 오차)

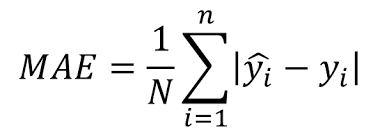
크로스엔트로피(Cross-entropy)
다항분포 로그손실(logloss)

여기서는 MSE를 사용하였다.

아래는 특성이 여러개인 경우의 MSE 수식이다.

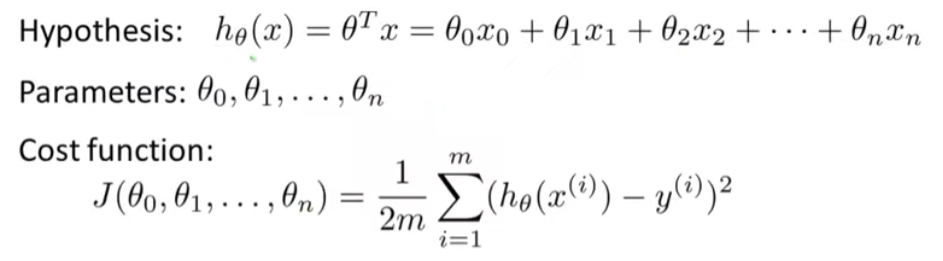
loss (가설 - 라벨)을 제곱
모두 합해준다.
2 * 샘플 개수로 나눈다.

cost = np.sum(loss ** 2) / (2 * m)
cost

25054.603702695855

3-5. 경사

경사, 즉 변화량를 구한다.

업데이트 할 때 마다 변화량이 점점 적어지고 결국에 변화량이 없다시피 하면 minimum에 도달했거나 running rate를 더 낮추어야 한다는 뜻이 된다.
(local minimum에, global minimum에 어느 것인지는 모름.)

변화량를 구하기 위해 편미분을 사용한다.

예전 알고리즘

새로운 알고리즘

https://www.youtube.com/watch?v=pkJjoro-b5c&list=PLLssT5z_DsK-h9vYZkQkYNWcItqhlRJLN&index=19

수식에서 $\alpha$ 는 학습률(running rate, alpha)를 뜻한다.

새로운 알고리즘의 내용을 보면

각 샘플과 샘플의 손실을 곱한다.
특성끼리 모두 합한다.
샘플 개수로 나눈다.

아래와 같은 방식으로 행렬곱이 이루어지고,
가중치 개수와 맞게 결과가 나온다.

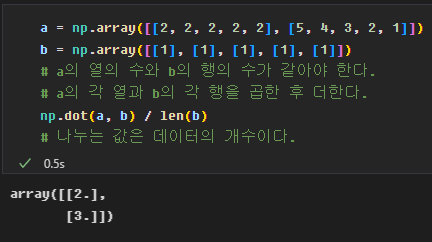
gradient = alpha * np.dot(xTrans, loss) / m
gradient

array([[0.38991081],
       [0.16512499]])

3-6. 가중치 업데이트

가중치에 변화량을 빼서 업데이트한다.

theta = theta - gradient
theta

array([[0.61008919],
       [0.83487501]])

3-7. 에포크 수 만큼 반복

배치 경사하강법은 에포크 수 만큼 업데이트를 반복한다.
샘플 1000개 / 에포크 5회일 경우,
5번의 업데이트가 일어난다.

확률적 경사하강법

배치 경사하강법과의 차이

확률적 경사하강법은 각 샘플마다 업데이트를 한다.
batchSize가 1인 경사하강법이다.
샘플 1000개 / 에포크 5회일 경우,
5000번의 업데이트가 일어난다.

코드

# 확률적 경사 하강법
def stochastic_gradient_descent(x : np.ndarray, y : np.ndarray, theta : np.ndarray, alpha : float, m : int, epoch : int, batchSize : int):
    xTrans = x.transpose()
    for i in range(0, epoch):
        for j in range(0, m):
            hypothesis = np.dot(x[j:j + 1, :], theta)
            loss = hypothesis - y[j:j + 1]
            cost = np.sum(loss ** 2) / (2 * m)
            gradient = alpha * np.dot(xTrans[:, j:j + 1], loss) / m
            theta = theta - gradient
    return ("확률적" , cost, theta)

미니 배치 경사하강법

배치 경사하강법과의 차이

미니 배치 경사하강법은 batchSize만큼 계산하여 업데이트 한다.
샘플 1000개 / 에포크 5회/ batchSize 10개일 경우,
500번의 업데이트가 일어난다.

코드

# 미니 배치 경사 하강법
def mini_batch_gradient_descent(x : np.ndarray, y : np.ndarray, theta : np.ndarray, alpha : float, m : int, epoch : int, batchSize : int):
    xTrans = x.transpose()
    for i in range(0, epoch):
        for j in range(0, m, batchSize):
            hypothesis = np.dot(x[j:j + batchSize, :], theta)
            loss = hypothesis - y[j:j + batchSize]
            cost = np.sum(loss ** 2) / (2 * m)
            gradient = alpha * np.dot(xTrans[:, j:j + batchSize], loss) / m
            theta = theta - gradient
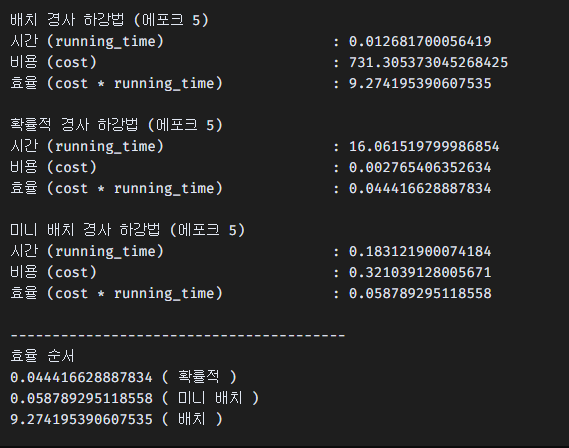
    return ("미니 배치" , cost, theta)

효율

시간은 짧을수록,
비용은 적을수록 좋기 때문에 두 값을 곱해서 낮을수록 좋은 효율이라는 점을 생각하여 계산해보았다.

확률적이 가장 우수하고,
미니 배치가 크지 않은 차이로 두번째,
배치 경사하강법이 가장 좋지 않았다.

다만 확률적은 시간이 매우 많이 걸리는 편이라,
범용적으로는 미니 배치가 좋을 것 같다.

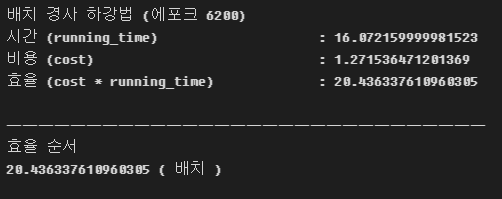
배치 경사하강법 테스트 추가

배치 경사하강법을 많이 돌리면 어떻게 될까.

위의 확률적 경사하강법과 비슷한 시간이 나오도록 세팅하고 테스트해보았다.

시간은 확률적과 동일하나, 비용이 많이 줄어들지 않아서 오히려 효율이 더 떨어졌다.

임의 테스트라서 정확하지 않을 수 있다.

미니 배치 경사하강법 테스트 추가

미니 배치 경사하강법도 확률적 경사하강법과 비슷한 시간이 나오도록 세팅하고 테스트 해보았다.

같은 시간 내에서 비용이 확률적보다 많이 줄어들었다.

임의 테스트라서 정확하지 않을 수 있다.

참고자료

소스코드
https://github.com/jaybon1/ai_practice/blob/master/009%EA%B2%BD%EC%82%AC%ED%95%98%EA%B0%95%EB%B2%95_%EB%B9%84%EA%B5%90.ipynb

Learning rate Decay의 종류
https://velog.io/@good159897/Learning-rate-Decay%EC%9D%98-%EC%A2%85%EB%A5%98

dot 참고
https://jimmy-ai.tistory.com/75

dot 참고 2
https://m.blog.naver.com/ssdyka/221300959357

비용함수, 손실함수, 목적함수
https://velog.io/@regista/%EB%B9%84%EC%9A%A9%ED%95%A8%EC%88%98Cost-Function-%EC%86%90%EC%8B%A4%ED%95%A8%EC%88%98Loss-function-%EB%AA%A9%EC%A0%81%ED%95%A8%EC%88%98Objective-Function-Ai-tech

비용함수와 경사 편미분
https://www.youtube.com/watch?v=pkJjoro-b5c&list=PLLssT5z_DsK-h9vYZkQkYNWcItqhlRJLN&index=19

jaybon

티스토리 블로그 https://ondolroom.tistory.com/

이전 포스트

경사하강법 - 3탄 (경사하강법 로직 및 분석)

머신러닝 정리

개요

경사하강법 로직을 보면서 이해하고, 성능 및 효율을 비교해본다.

코드 설명 (배치 경사하강법)

전체코드

0. 라이브러리 import

1. 데이터 로드

2. 데이터 세팅

2-1. 특성

2-2. 라벨

2-3. 샘플 개수와 특성 개수

2-4. 에포크

2-4. 임의 가중치

2-5. 학습률

2-6. 배치 사이즈

3. 경사하강 함수

3-1. 특성 pivot

3-2. 예측값 (가설)

3-3. 손실 (잔차)

3-4. 비용

3-5. 경사

예전 알고리즘

새로운 알고리즘

3-6. 가중치 업데이트

3-7. 에포크 수 만큼 반복

확률적 경사하강법

배치 경사하강법과의 차이

코드

미니 배치 경사하강법

배치 경사하강법과의 차이

코드

효율

배치 경사하강법 테스트 추가

미니 배치 경사하강법 테스트 추가

참고자료

경사하강법 - 2탄 (확률적의 의미)

0개의 댓글