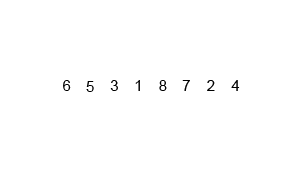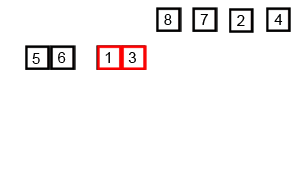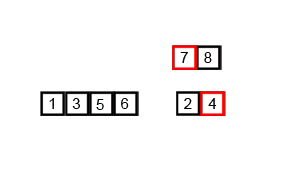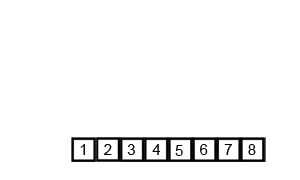정렬 알고리즘
n개의 숫자가 저장된 배열이 주어졌을 때, 사용자가 지정한 기준에 따라 이를 정렬하는 알고리즘
- 단순하지만 비효율적인 방법 : 삽입 정렬, 선택 정렬, 버블 정렬
- 복잡하지만 효율적인 방법 : 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬
정렬 알고리즘에는 다양한 종류가 있지만,
해당 글에서는 총 7가지의 정렬만 다루려고 한다.
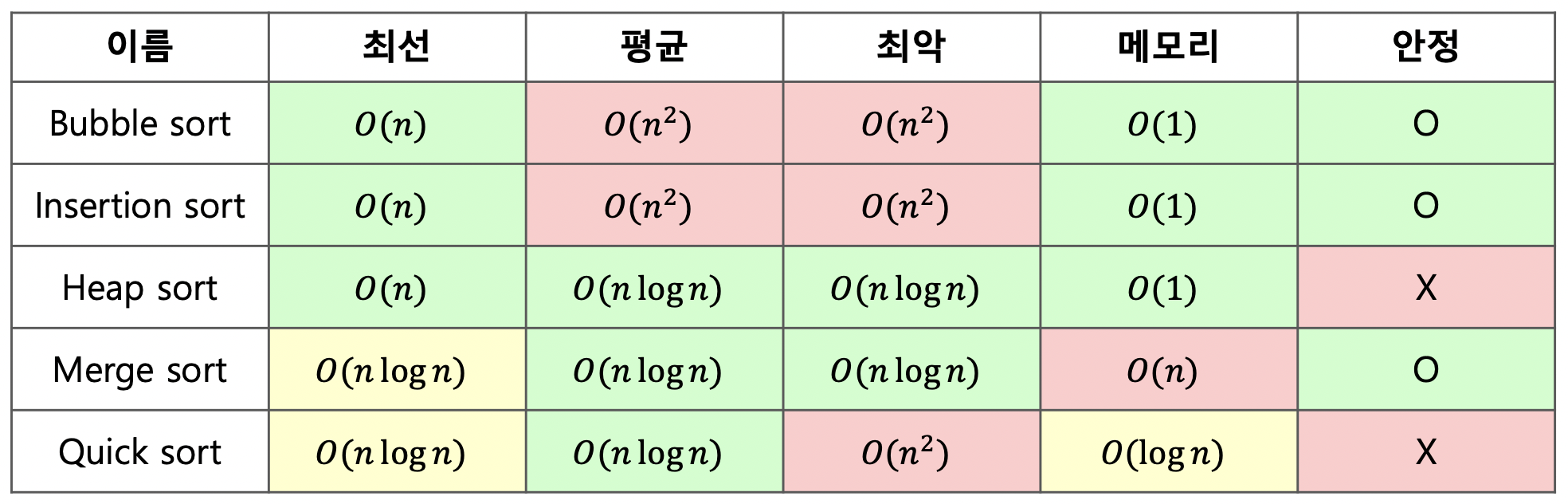
그 중 5가지의 경우를 정리한 표는 아래와 같다
🔎 삽입 정렬 ; Insertion sort
가장 간단한 정렬 방식
이미 순서화된 파일에 새로운 하나의 레코드를 순서에 맞게 삽입시켜 정렬
시간 복잡도는 평균과 최악 모두 O(n^2)이다.
✅ 로직
- 두 번째 인덱스부터 시작
- 인덱스를 기준으로 왼쪽 끝까지 비교해가면서
- 인덱스가 왼쪽 값보다 크면 자리 교환
- 마지막 인덱스까지 진행
삽입 정렬의 예시를 함께 보자.
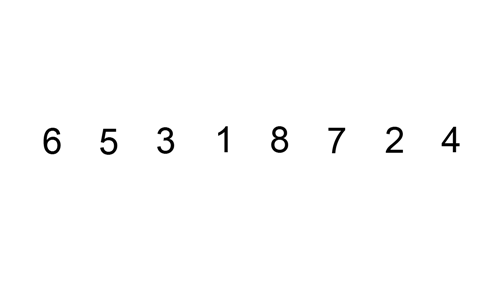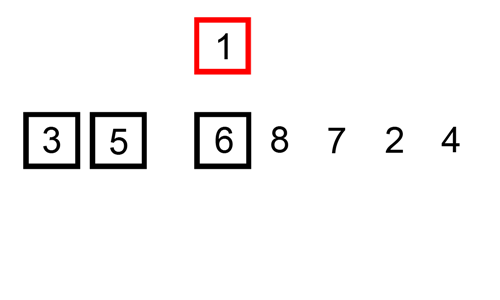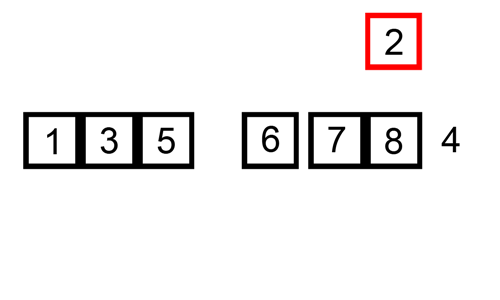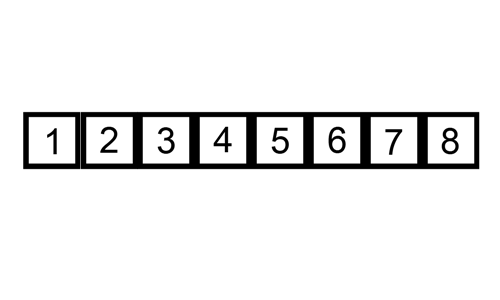
🔎 쉘 정렬 ; Shell sort
삽입 정렬을 확장한 개념 (보완)
Donald L. Shell이라는 사람이 제안한 방법이다.
삽입 정렬과 다르게 셸 정렬은 전체의 리스트를 한 번에 정렬하지 않는다.
시간 복잡도는 평균의 경우 O(n^1.5), 최악의 경우 O(n^2)이다.
✅ 로직
- 정렬해야 할 리스트를 일정한 기준에 따라 분류
- 연속적이지 않은 여러 개의 부분 리스트를 생성
- 각 부분 리스트를 삽입 정렬을 이용하여 정렬
- 모든 부분 리스트가 정렬되면 다시 전체 리스트를 더 적은 개수의 부분 리스트로 만든 후에 알고리즘을 반복
- 위의 과정을 부분 리스트의 개수가 1이 될 때까지 반복
쉘 정렬의 진행 방식을 함께 보자.
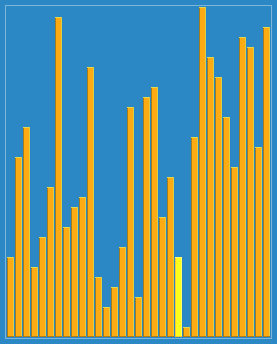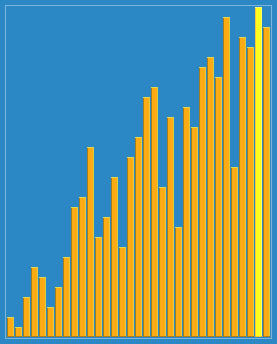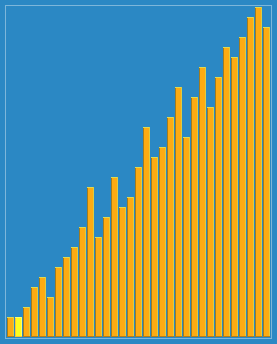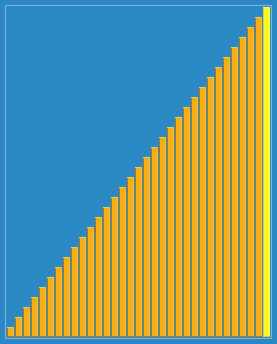
🔎 선택 정렬 ; Selection sort
전체 중 최소 값을 찾아 첫 번째 위치로 놓는 것을 반복하여 정렬하는 방식
시간 복잡도는 평균과 최악 모두 O(n^2)이다.
✅ 로직
- 첫 번째 인덱스와 나머지 인덱스를 비교해서 최소값을 찾아 자리를 교환
- 그런 다음, 두 번째 인덱스와 나머지 인덱스(정렬 된 첫번째 인덱스 제외)를
비교해서 최소값을 찾아 자리를 교환 - 위의 과정을 정렬을 끝마칠 때 까지 반복
선택 정렬의 진행 방식을 함께 보자.

🔎 버블 정렬 ; Bubble sort
연속 된 두 개 인덱스를 비교, 정한 기준의 값을 뒤로 넘겨 정렬하는 방식
시간 복잡도는 평균과 최악 모두 O(n^2)이다.
✅ 로직
- 첫 번째 인덱스와 두 번째 인덱스를 비교, 큰 값을 뒤로
- 두 번째 인덱스와 세 번째 인덱스를 비교, 이를 정렬 끝까지 반복
- 끝에 도달하면 1회전 끝,
- 이를 (전체 배열의 크기 - 현재까지 순환한 바퀴의 수) 까지 반복
버블 정렬의 진행 방식을 함께 보자.
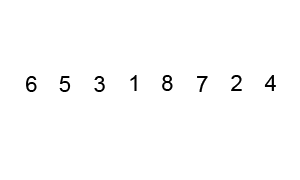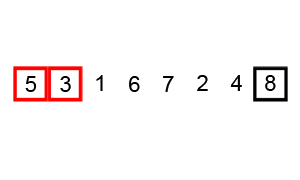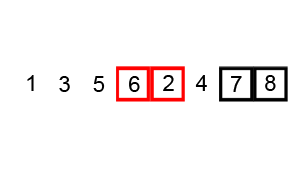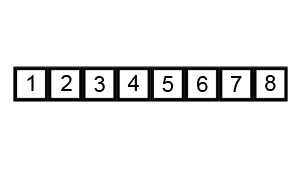
🔎 퀵 정렬 ; Quick sort
레코드의 많은 자료 이동을 없애고 하나의 파일을 부분적으로 나누어 가면서 정렬
분할과 정렬을 동시에 진행
시간 복잡도는 평균의 경우 O(nlogn), 최악의 경우 O(n^2)이다.
✅ 로직
- 리스트에 있는 임의의 한 요소를 선택 ; 피벗(pivot)
- 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로,
피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 - 피벗을 제외한 왼쪽, 오른쪽 리스트를 다시 퀵 정렬
- 더 이상 분할할 수 없을 때 까지 진행
퀵 정렬의 진행 방식을 함께 보자.
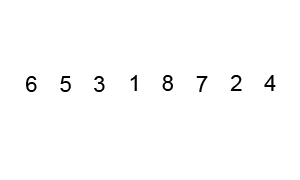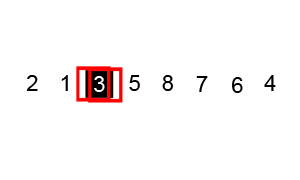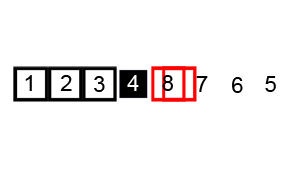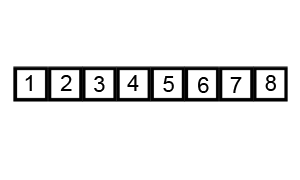
🔎 힙 정렬 ; Heap sort
전이진 트리(Complete Binart Tree)를 이용한 정렬 방식
시간 복잡도는 평균과 최악 모두 O(nlogn)이다.
✅ 로직
힙 정렬의 진행은 글로 설명하는 것 보단 눈으로 보는 게 이해가 더 빠르다.

🔎 2-Way 합병 정렬 ; Merge sort
이미 정렬되어 있는 두 개의 파일을 한 개의 파일로 합병하는 정렬 방식
시간 복잡도는 평균과 최악 모두 O(nlogn)이다.
✅ 로직
- 숫자를 두개씩 한 쌍으로 묶는다.
- 정렬한다.
- 정렬 된 묶음들을 다시 두 묶음씩 한 쌍으로 묶는다.
- 숫자의 쌍이 리스트 전체가 될 때 까지 반복
머지 정렬의 진행 방식을 함께 보자.