프로젝트 끝나고 약 한 달여만에 건드리는 알고뤼듬~!
알고리즘 풀이를 관장하는 두뇌 근육이 오랫동안 자다 깨서인지 알고리즘 푸는게 더 오래 걸리고 더 어렵게 느껴진다. (원래 이랬을지도? ㅋㅋㅋㅋ)
다시 하루에 2문제 씩 풀면서 얼른 회복하자!!

문제

계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.

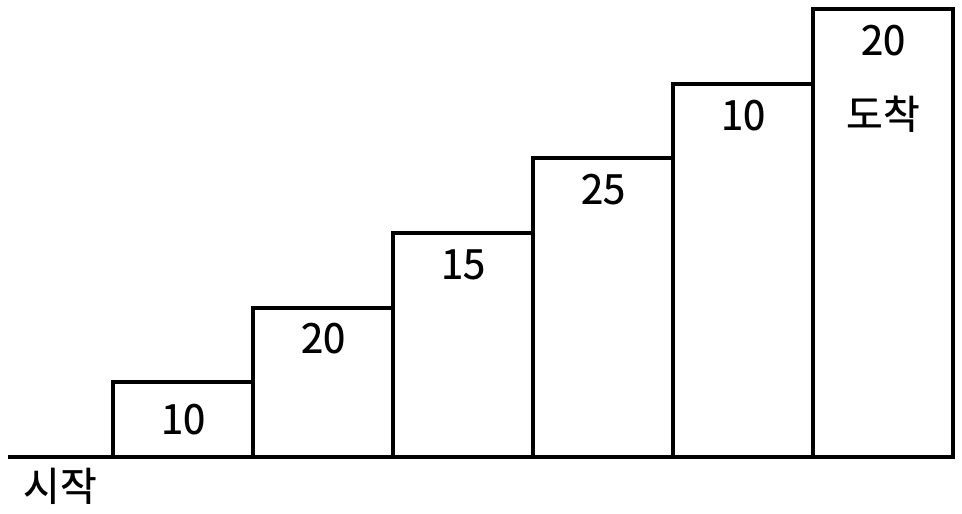
<그림 1>

예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.

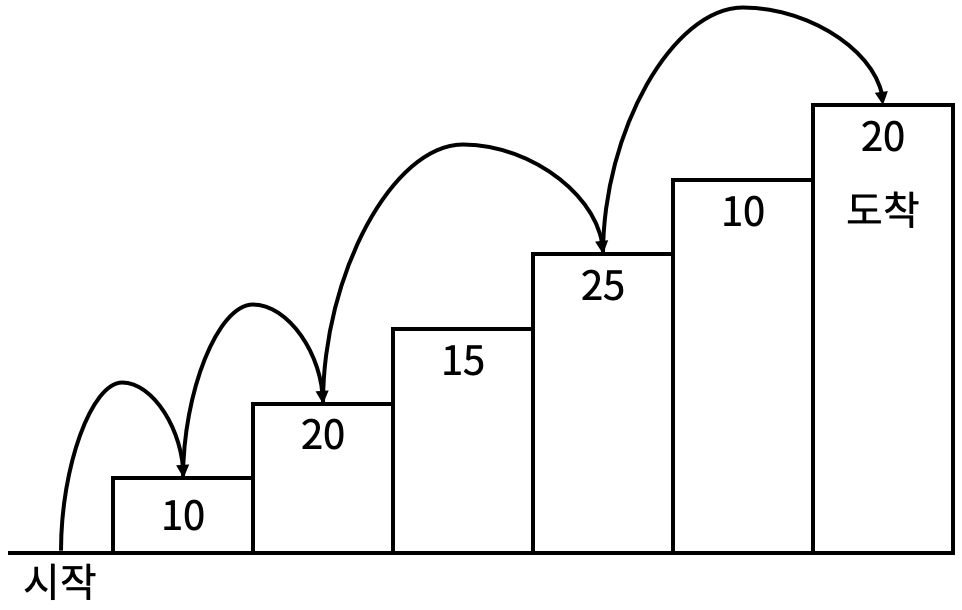
<그림 2>

계단 오르는 데는 다음과 같은 규칙이 있다.

계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.

각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.

입력

입력의 첫째 줄에 계단의 개수가 주어진다.

둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.

출력

첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.

예제 입력 1

6
10
20
15
25
10
20

예제 출력 1

75

실패했던 코드 💩

from sys import stdin as s

# s = open("input.txt", "rt")  # 주석 처리해야 하는 부분

n = int(s.readline())

stairs = [0] * 302

for i in range(1, n + 1):
    stairs[i] = int(s.readline())

dp = [0] * 302
dp[1] = stairs[1]
dp[2] = stairs[1] + stairs[2]

for i in range(3, n + 1):
    # 2가지 option이 있다. 하나는 직전 2개 중 하나를 버리고 이번 계단을 밟는 것.
    option1 = dp[i-3] + max(stairs[i-2], stairs[i-1]) + stairs[i]
    # 다른 하나는 이번 계단을 버리고 다음 계단을 밟는 것.
    option2 = dp[i-1] + stairs[i+1]
    if (option1 > option2):
        # 이번 계단을 밟는다. (직전 2개 중 하나를 버린다.)
        dp[i] = option1
    else:
        # 이번 계단을 밟지 않는다.
        dp[i] = dp[i-1]

# 그럼 마지막 계단이 선택이 안되면 얶떡켸 함?
print(dp[n])

마지막 계단을 반드시 밟아야 한다.

이 문장이 이 문제를 해결하는 핵심 포인트였다.

마지막 계단을 반드시 밟아야 한다.
==
for 문을 돌릴 때 매 회차마다 i번째 계단은 반드시 밟는다고 전제해라.

처음에 실패했던 이유는 이 전제를 생각하지 못했기 때문이었다.
현재 계단을 밟을지 말지를 선택하는 문제일것이라고 잘못 생각했다.

만약 현재 계단을 밟을지 말지로 접근하면 마지막 계단이 선택되지 않을 가능성이 있으므로
마지막 계단을 반드시 밟아야 한다는 문제의 규칙에 위배된다.

따라서 통과한 코드는 아래와 같다.

통과 코드 ✅

from sys import stdin as s

s = open("input.txt", "rt")  # 주석 처리해야 하는 부분

n = int(s.readline())

stairs = [0] * 301

for i in range(1, n + 1):
    stairs[i] = int(s.readline())

dp = [0] * 301
dp[1] = stairs[1]
dp[2] = stairs[1] + stairs[2]

for i in range(3, n + 1):
    # 2가지 option이 있다.
    # 전제: i번째 계단을 밟는다.
    # i-1 번째 계단 포기
    option1 = dp[i-2]
    # i-2 번째 계단 포기
    option2 = dp[i-3] + stairs[i-1]
    dp[i] = max(option1, option2) + stairs[i]

print(dp[n])

이렇게 하면 매 회차마다 i번째 계단은 반드시 선택하게 된다.
이에 따라 n번째 계단도 반드시 선택하게 된다.

그리고 이번 계단을 반드시 선택하려면
i-1번째 계단과 i-2번째 계단 중 둘 중 하나는 반드시 포기해야 한다. (둘 다 선택 불가능)

i번째 회차에 들어섰을 때 i-1번째 계단은 반드시 선택된 상태일 것이다.

그럼 i-2번째 계단은?
선택이 되었을 수도 있고 이전에 포기했을 수도 있다.
만약 i-2번째 계단이 선택되었다면 dp[i-3]번째 + stair[i-2]번째만큼 합산된 값이 들어가 있을 것이고
선택되지 않았다면 dp[i-3]과 동일한 숫자가 들어있을 것이다.

그렇다면 i-2번째 계단을 포기하고 i-1번째 계단을 선택한다면? i번째 계단을 밟는데 문제 없다.
근데 i-2번째 계단을 선택하고 i-1번째 계단을 포기한다면?
i-2번째 계단을 이전에 포기했을수도 있다며?
그래서 option2는 dp[i-2]가 아니라, dp[i-3] + stairs[i-1]로 갱신하여 표현한 것이다.

일단 생각한대로 + 이해한대로 열심히 쓰긴 했는데.. 오랜만에 알고리즘 포스팅하는 거라 나도 내가 제대로 쓰고 있긴 한건지 확신이 없는걸? ㅋㅋㅋ 틀린 부분 있으면 지적 환영합니다!!!