학습 참고 자료
⭐ 시뮬레이션 해 볼 수 있다!
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
트리 개념 점검하기!
- 트리의 차수 (degree)
: 트리의 최대 차수 (※차수 : 한 노드에 연결된 자식 노드(or 서브 트리)의 갯수) - 트리의 높이/깊이 (height/depth)
: 루트 노드부터 단말 노드까지의 경로 길이 ⇒ 즉, 엣지의 갯수 (= 레벨) - 이진 트리 종류
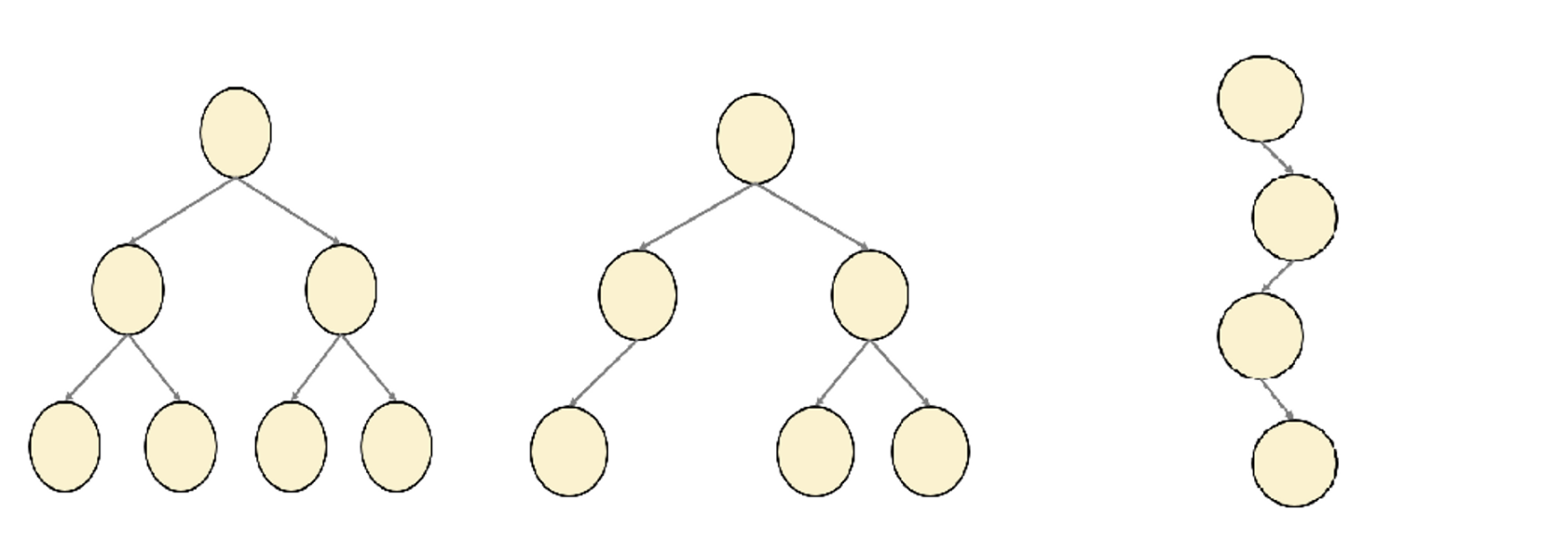
1) 완전이진트리 (Complete Binary Tree)
- 모든 노드가 2개의 자식을 가진다.
- 마지막 레벨을 제외하고, 모든 레벨은 완전히 채워져 있다.
- 마지막 레벨의 모든 노드는 왼쪽부터 채워져 있다.
2) 균형이진트리 (Balance Binary Tree)
- 모든 노드의 왼쪽과 오른쪽 하위 트리와의 높이가1 이상 차이 나지 않는다.☞ 1 이상 차이 나지 않는 걸 ‘지향’한다. (더 차이날 수 있음)
3) 변질트리 (Degenerate Tree)
- 각 부모 노드는 오직 하나의 자식 노드를 갖는다.
- 연결 리스트처럼 동작함
1. R-B 트리 개념
- 이진탐색트리(BST)의 한 종류로, 자가균형이진탐색트리라고도 할 수 있다.
- 즉, 노드의 삽입과 삭제 시 자동으로 (일정 부분) 균형을 맞춰준다!
- BST 최악의 경우 (변질트리. O(N) 소요) → 이를 보완하기 위해 등장했다.
- 따라서, BST의 특성 + R-B 트리만의 속성(5가지)를 갖춰야 한다.
- 최악의 경우에도 시간복잡도는 O(logN)
- Black-Height
: 임의의 노드부터 리프 노드까지 black 노드의 갯수 → 5번 속성을 점검하기 위해 필요하다!
d2 ≥ d1 * 2를 성립한다. (동일한 Black Height 유지한다는 전제)
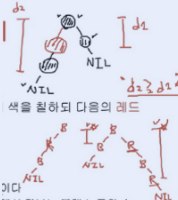 → 왼쪽이 black으로만 이뤄져 있고, 오른쪽은 black과 red가 번갈아 있을 때를 보여준다. 즉, 왼쪽과 오른쪽 서브트리의 depth는 최대 2배까지만 차이 난다.
→ 왼쪽이 black으로만 이뤄져 있고, 오른쪽은 black과 red가 번갈아 있을 때를 보여준다. 즉, 왼쪽과 오른쪽 서브트리의 depth는 최대 2배까지만 차이 난다.
2. R-B 트리의 5가지 속성 ⭐
첫째, 모든 노드는 red or black
둘째, 루트 노드는 black
셋째, 리프(NIL) 노드는 black
넷째, double red는 불가능 (red 노드의 자식은 black만 가능하다.)
다섯째,각 노드에서 리프 노드까지, black 노드의 수는 항상 같아야 한다.
(임의의 모든 노드에 대해 Black Height가 동일해야 한다. 자기 자신은 카운트에서 제외)
※
NIL: 존재하지 않음을 의미하는 노드 (즉, 자녀가 없다는 의미)
→ R-B 트리에서 모든 리프노드는 NIL 노드이다!
3. RB 트리 연산 (1) : 삽입
💡 전제 : RB트리의 속성 5가지를 만족하고 있으며, 삽입하는 노드는 red (B-H 때문!)
step 1. BST의 방식으로 노드를 삽입한다.
step 2. 속성 5가지를 확인한다.
step 3. 위배되는 속성이 있으면, 이를 해결한다. (재조정)⇒ RB 트리를 만족한다. (반복)
2번 속성을 위반했을 때
👉 부모 노드를 black으로 바꿔준다.
4번 속성을 위반했을 때
-
삼촌 노드의 색이
red인 경우
👉 Recoloring + 자식-부모-할아버지를 정렬하고 가운데 값을 기준으로 트리를 만들어 재배치한다. -
삼촌 노드의 색이
black인 경우
👉 Restructing + 자식-부모-할아버지를 정렬하고 가운데 값을 기준으로 트리를 만들어 재배치한다.
4. RB 트리 연산 (2) : 삭제
💡 전제 : RB트리의 속성 5가지를 만족하고 있다.
step 1. 대상 노드를 삭제한다.
step 2. 삭제 후, 속성 5가지를 확인한다.
step 3. 위배되는 속성이 있으면, 이를 해결한다. (재조정)⇒ RB 트리를 만족한다. (반복)
R-B 트리의 특정 노드를 삭제하는 과정은 조금 복잡한데..
우선, 문제가 되는 경우와 문제가 되지 않는 경우로 나눠볼 수 있다.
👍 문제가 되지 않는 경우
문제가 되지 않는 경우란, (노드) 대이동이 필요 없는 경우이다.
즉, BST 삭제와 동일하게 진행되지만(부모 자리에 적절한 자식이 들어옴 + 적절한 색으로 칠해짐) 그 주변부의 변경은 필요 없는 케이스이다.
삭제 노드의 자식이 2개인 경우는, 항상 문제 되지 않는다고 보면 된다.
반면, 삭제 노드의 자식이 없거나 1개만은 가지는 경우는 이야기가 달라지는데, 이 상황을 놓고 설명하겠다. (즉, 삭제 노드 m에 대해 자식이 1개 또는 없는 경우로만 제한하겠다.)
따라서, 문제가 되지 않는 경우는 다음과 같다.
- 삭제 노드가
red인 경우 - 삭제 노드가
black이더라도 (유일한) 자식이red인 경우
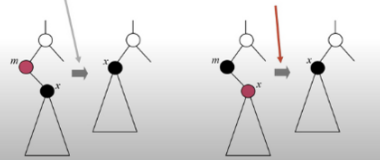
👎 문제가 되는 경우 : (노드) 대이동이 필요하다.
- 삭제 (하려는) 노드 m과 자식 노드 x 둘 다
black인 경우
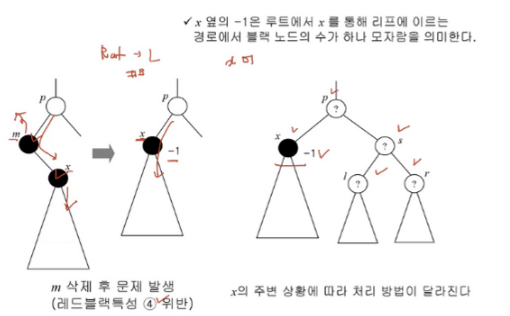
위의 경우, (동일해야 하는) Black Height에 오류가 생긴다!
결국,
삭제 노드의 서브트리-부모 노드-형제 노드 서브트리간에
Black Height를 동일하게 맞추는 것이 삭제 연산의 관건이 되며,"존재할 수 있는 나머지 노드들에 대해 어떻게 처리할 것인지?"가 기준이 된다.
그리고 이에 따라 케이스를 분류할 수 있고, 각 케이스별로 해결방안을 찾아볼 수 있다.
고고씽
step 1. 경우의 수 나누기 : CASE 1 / CASE 2
삭제된 지점(노드)의 부모 노드를 p라 할 때, red / black 색상에 따라 두 가지 케이스로 분류한다.
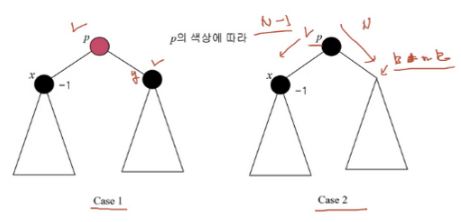 그리고 이 두 분류에 따라 문제가 되는 케이스를 7가지로 나눠볼 수 있는데..
그리고 이 두 분류에 따라 문제가 되는 케이스를 7가지로 나눠볼 수 있는데..
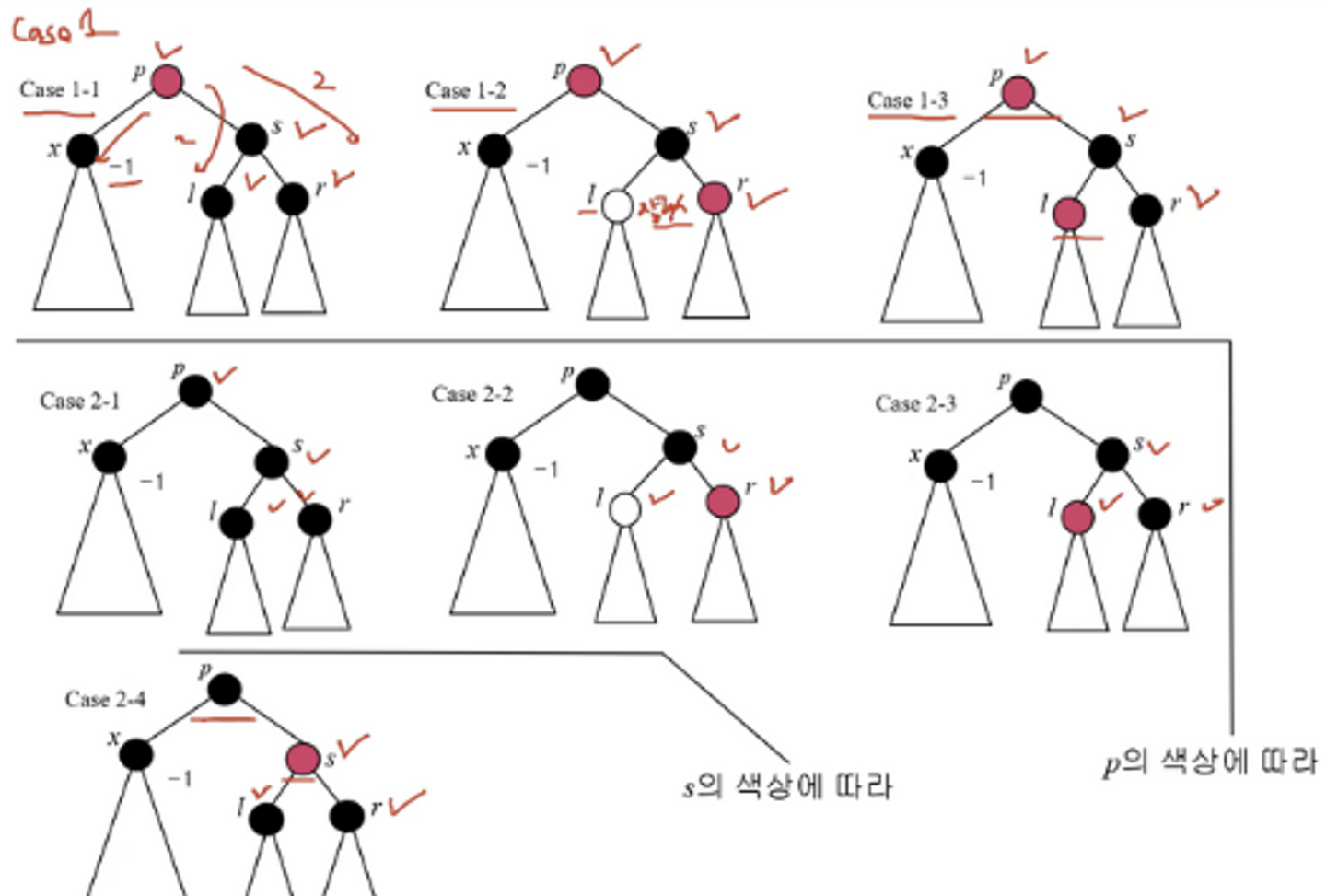 이렇게 나뉜다. 근데 이 중에서 중복된 걸 정리하면, 최종적으로 5가지 케이스로 분류할 수 있다. 그리고 이 5가지 케이스를 기준으로 R-B 트리의 삭제 연산 과정을 분류하겠다.
이렇게 나뉜다. 근데 이 중에서 중복된 걸 정리하면, 최종적으로 5가지 케이스로 분류할 수 있다. 그리고 이 5가지 케이스를 기준으로 R-B 트리의 삭제 연산 과정을 분류하겠다.
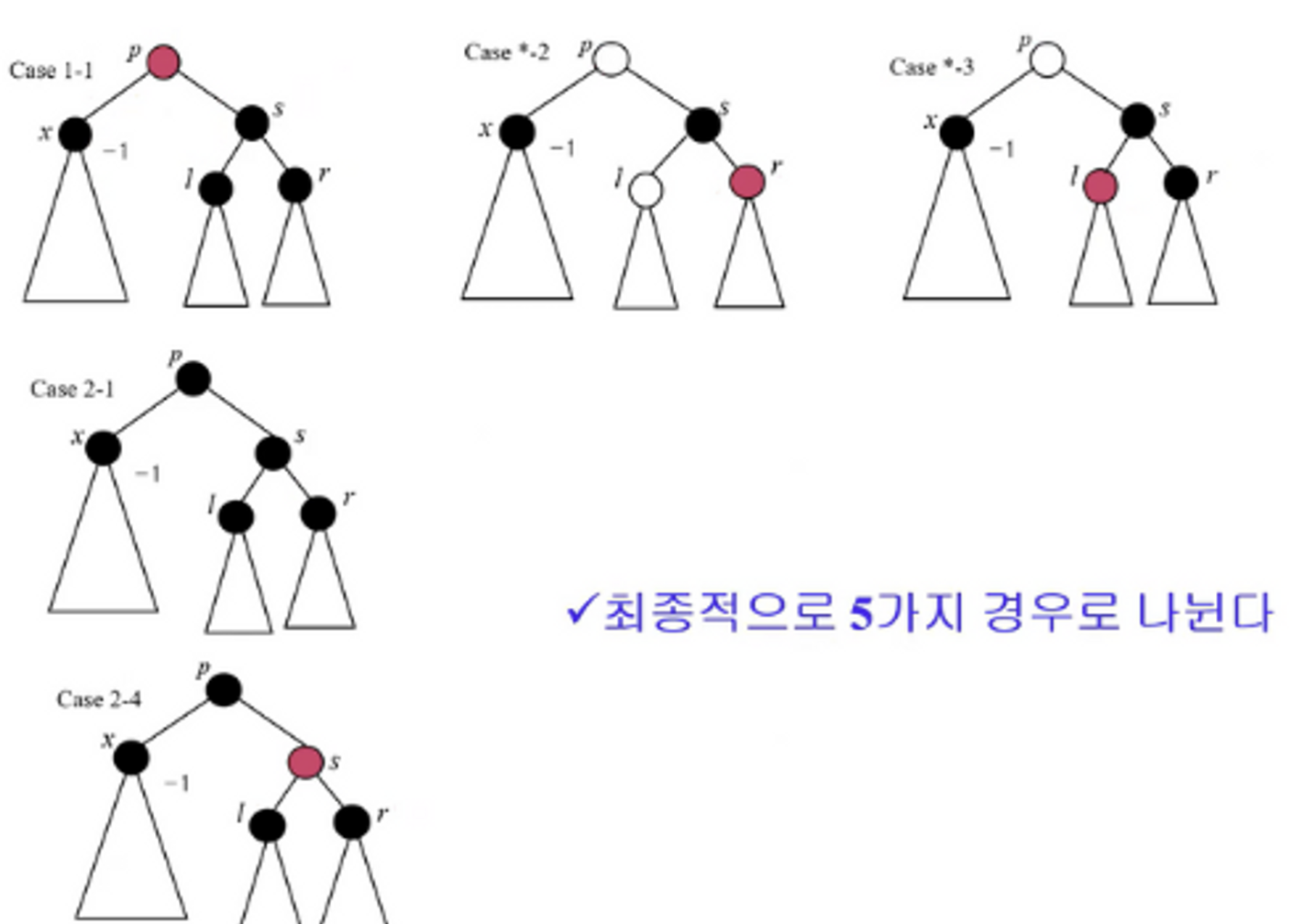
x + 왼쪽 서브트리 : m 노드가 삭제되고, 그 자리에 자식 x가 들어와 있다. B-H는 value-1로, 1 감소되어 있다.
p : m 노드의 부모 노드이다.
s : m 노드의 형제 노드 서브 트리이다. B-H는 value이다.
case 1-1
👉 p와 s의 색을 바꾼다.!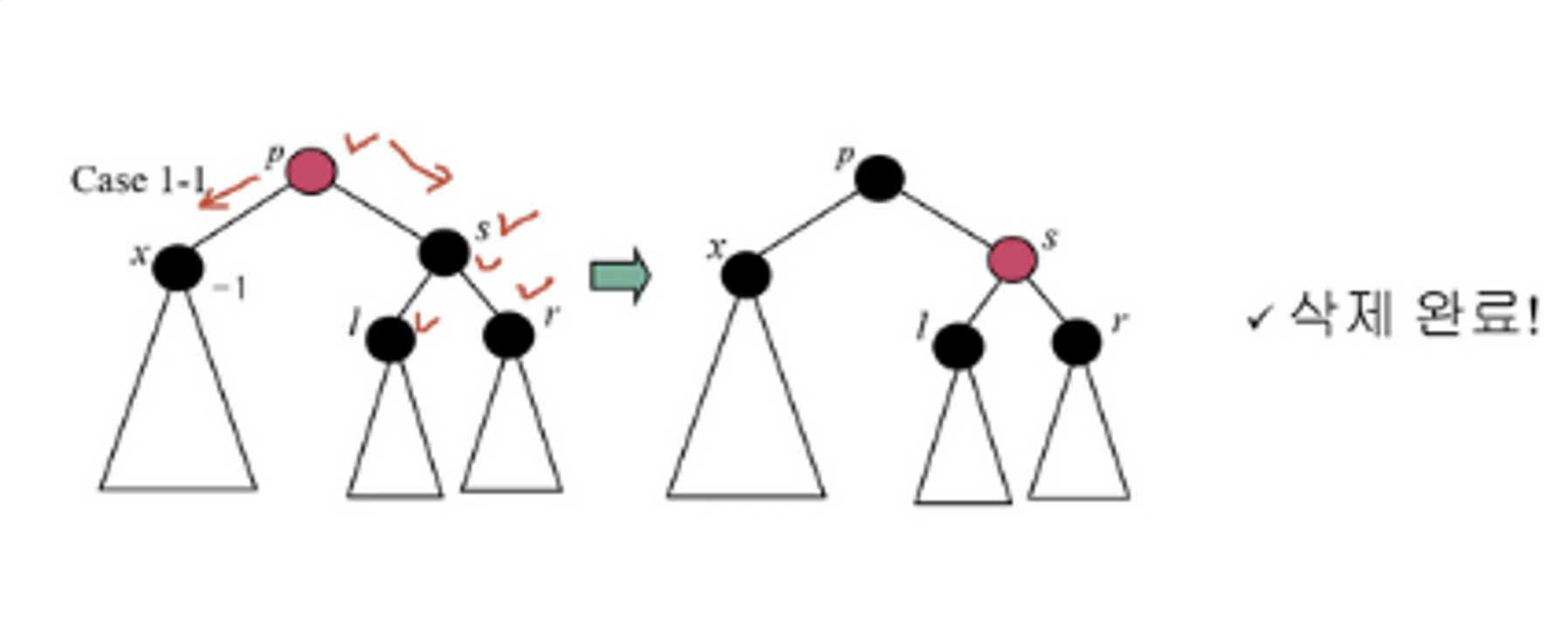
case *-2
👉 반시계 방향으로 회전한다. → s의 색은 상관 없지만, 이전 p의 색에 맞춰 바꾼다. 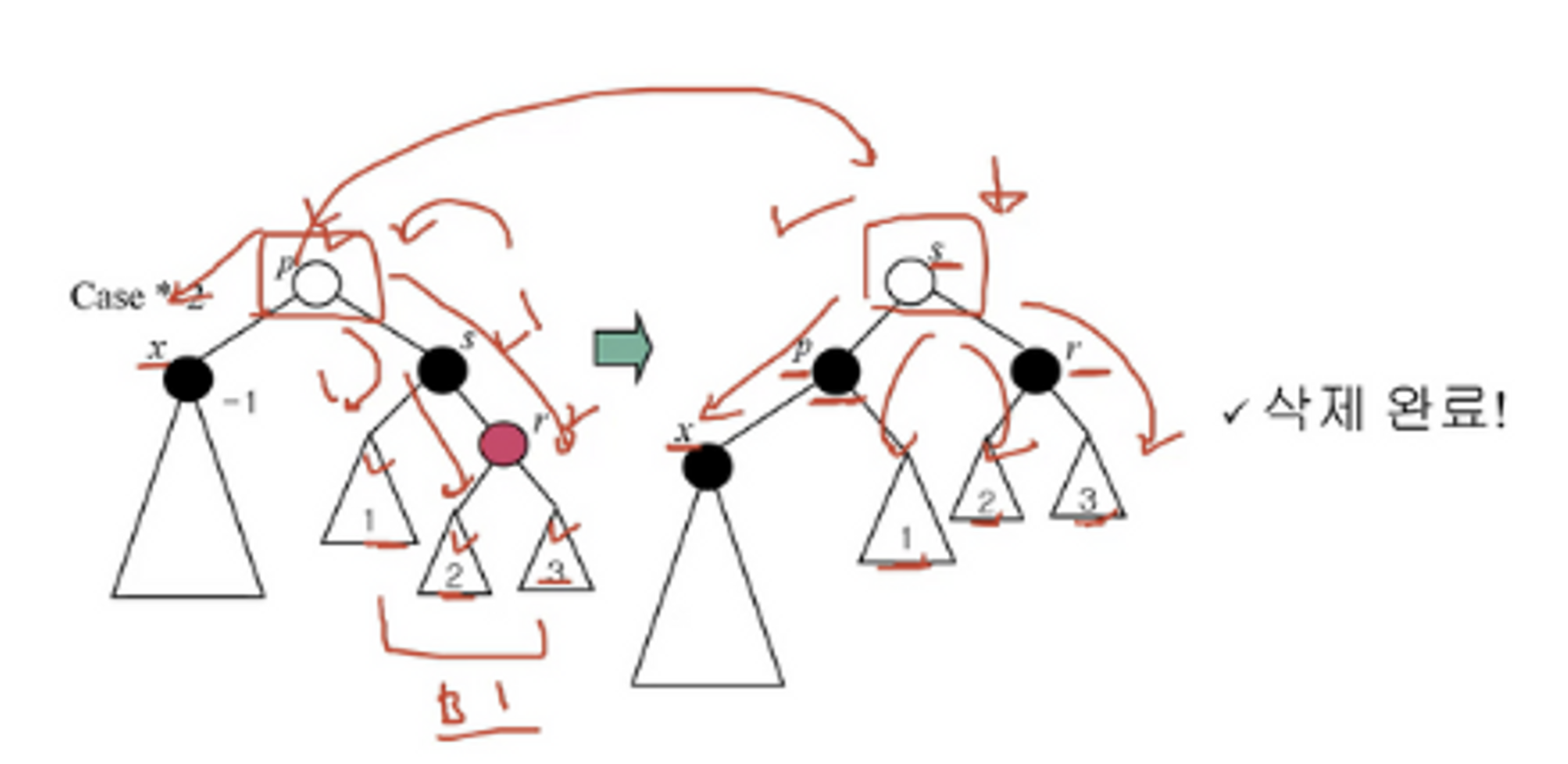
case *-3
👉 l을 s 기준 시계방향으로 한 번 회전하고 → 서브트리 1과 2를 맞춰주고 → case *-2 단계로 처리한다. 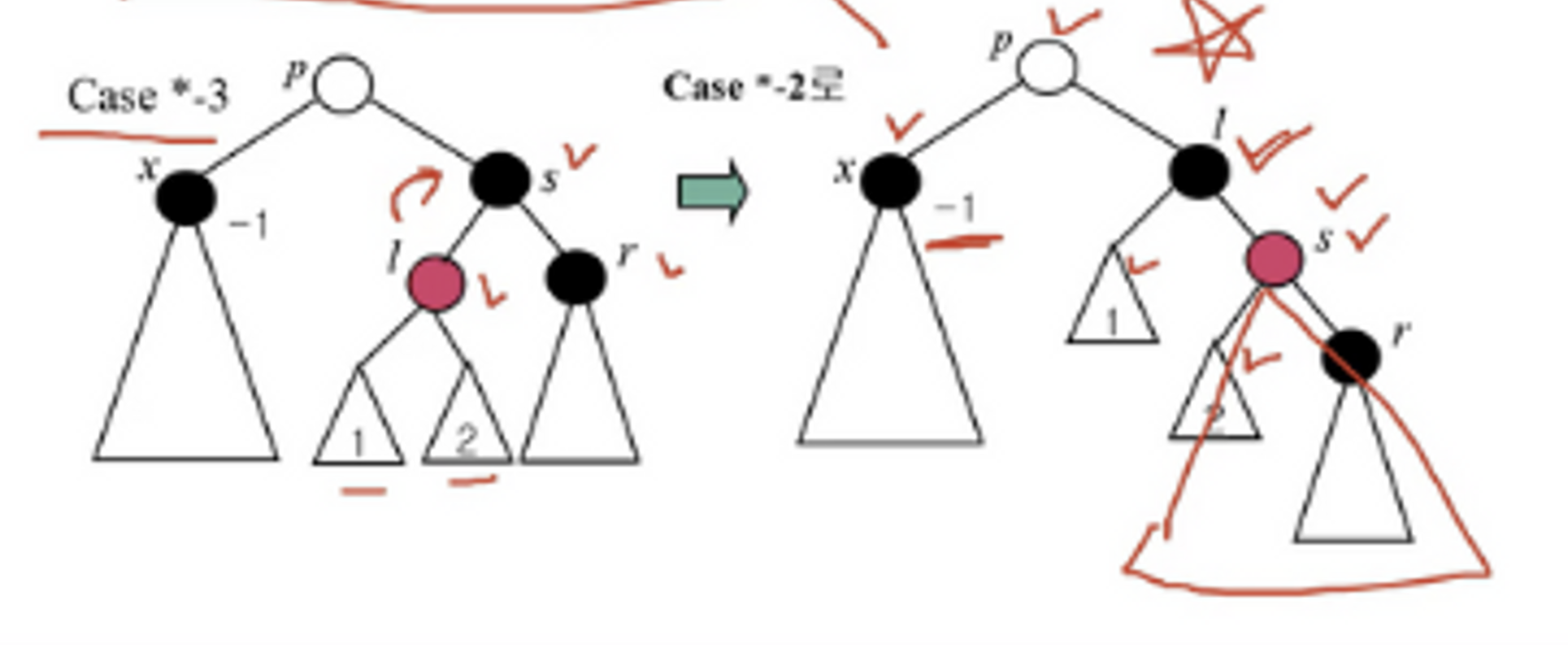
case 2-1.
👉 모든 노드가 black인 경우로, s를 red로 바꾼다. 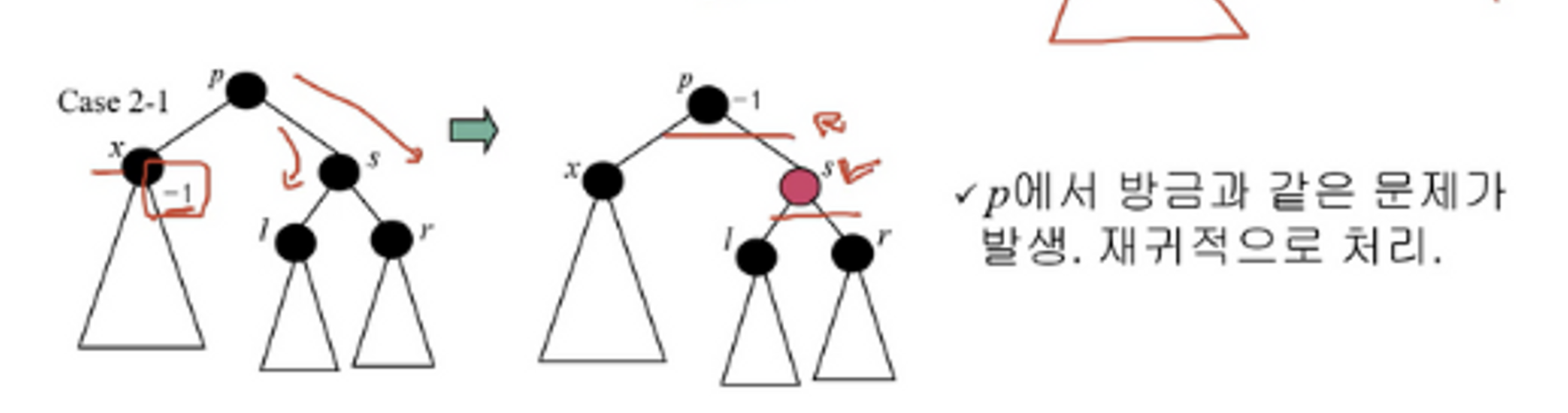
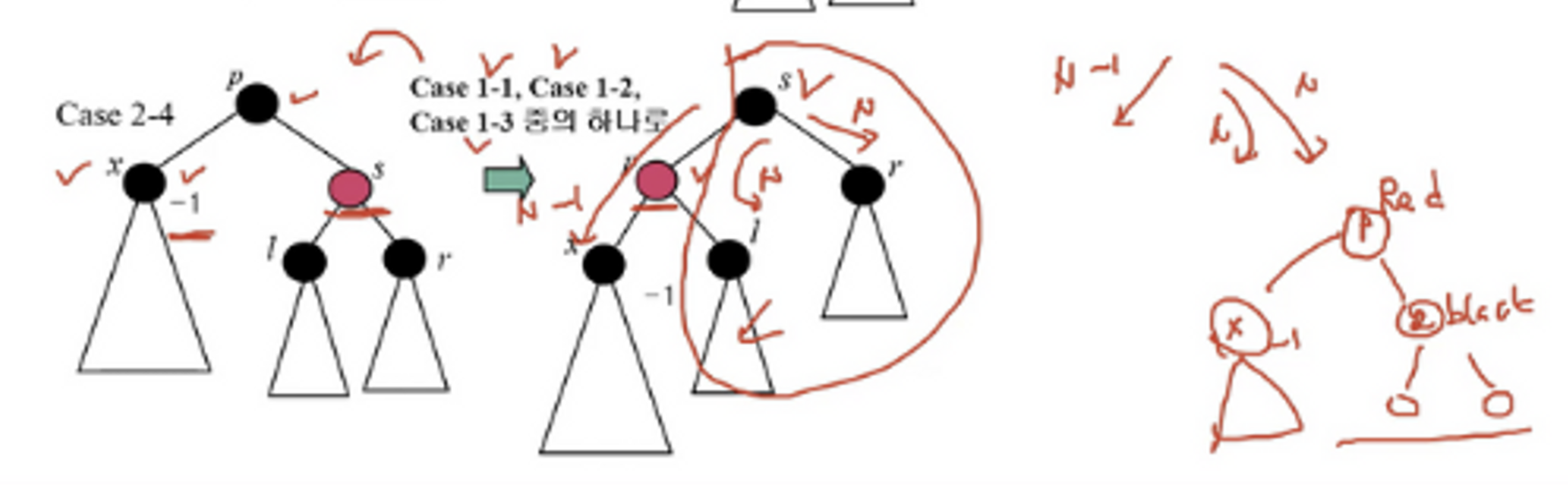
case 2-4.
👉 s가 유일하게 red인 경우로, 반시계 방향으로 회전시킨다. → 조카 노드의 색에 따라서 case 1-1, -2, -3 중에 하나로 처리한다.