[ 이분탐색(이진탐색) ]
“데이터를 검색하는 방법”
1. 개념 : 사과 속 씨 찾기
“반씩 쪼개고 찾자!”
문제 → 과정 → 리턴
- 문제 : 정렬된 리스트 S에 어떤 키 x가 존재하는가?
- 전제 : 정렬된 리스트여야 한다. (정렬되어 있지 않은 경우는 ‘순차 탐색’)
- 과정 : 배열의 중앙값으로부터 작으면 왼쪽 이동 (오른쪽 버리기) / 크면 오른쪽 이동 (왼쪽 버리기)
- 리턴 : (존재 O) S에서 x의 위치 / (존재 X) 0 or 특정 값 리턴
2. 원리
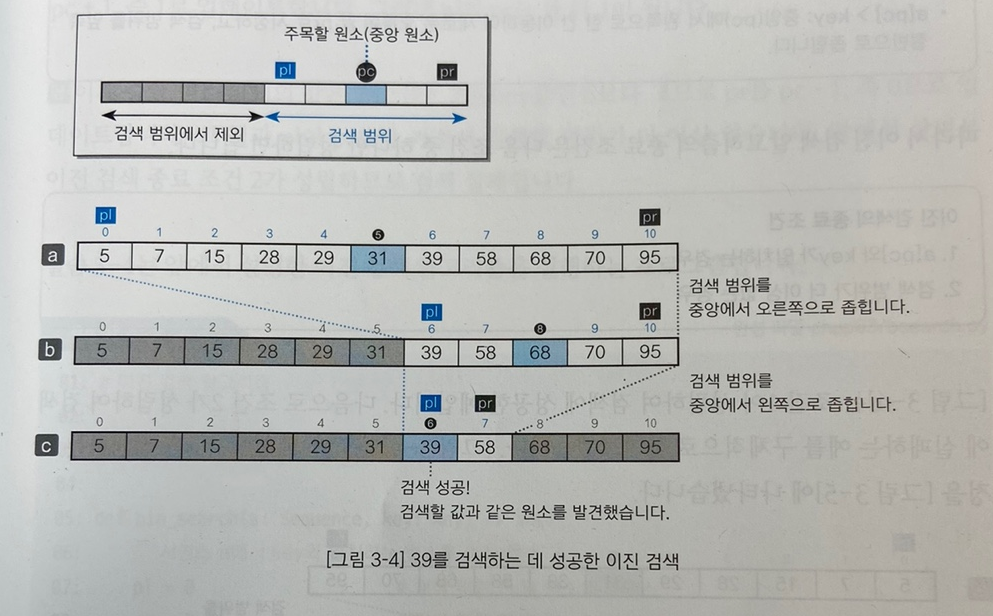
- 필요한 데이터 : pl / pr / pc 인덱스 → 배열의 첫 번째 / 배열의 마지막 / 배열의 중간((pl + pr) // 2)
1) a[pc]와 key 값을 비교한다.
2) a[pc] < key 이면 → pl = pc + 1 / pr = pr → 왼쪽 버리고 → pc + 1 ~ pr에서 찾기! a[pc] > key 이면 → pl = pl / pr = pc - 1 → 오른쪽 버리고 → pl ~ pc - 1에서 찾기!
3) a[pc] == key가 될 때까지 2번 과정을 반복한다.
(혹은 검색범위가 더 이상 없는 경우, 끝난다.)
3. 대표적인 알고리즘
1) 반복문
from typing import Any, Sequence
# 이진 검색 알고리즘
def bin_search(a: Sequence, key: Any) -> int:
"""시퀀스 a에서 key와 일치하는 원소를 이진 검색"""
pl = 0 # 검색 범위 맨 앞 원소의 인덱스
pr = len(a) - 1 # 검색 범위 맨 끝 원소의 인덱스
while True:
pc = (pl + pr) // 2 # 중앙 원소의 인덱스
if a[pc] == key:
return pc # 검색 성공
elif a[pc] < key:
pl = pc + 1 # 검색 범위를 뒤쪽 절반으로 좁힘
else:
pr = pc - 1 # 검색 범위를 앞쪽 절반으로 좁힘
if pl > pr: # key가 없음 (검색 실패)
return -12) 재귀함수
from typing import Any, Sequence
# 이진 검색 알고리즘
def bin_search(a: Sequence, key: Any, pl: int, pr: int) -> int:
pc = (pl + pr) // 2
if pl > pr: # key가 없음 (검색 실패)
return -1
if a[pc] == key:
return pc # 검색 성공
elif a[pc] < key:
return bin_search(a, key, pc + 1, pr) # 검색 범위를 뒤쪽 절반으로 좁힘
else:
return bin_search(a, key, pl, pc - 1) # 검색 범위를 앞쪽 절반으로 좁힘
※ 이미 (오름차순으로) 정렬된 리스트에 한해서 가능하다. (sort 함수 사용 or 입력 시 이전 원소보다 크게끔 설정)
⭐ 시간복잡도는 O(logN)
4. 특징/장단점
- 장점 :데이터에서 특정한 값을 빠르게 찾을 수 있다. (선형 탐색에 비해)
- 단점
- 미리 오름차순으로 정렬되어 있어야 한다.
- 경우에 따라서는 쓰기 곤란한다. ex. 연결 리스트 (자기테이프 같은 구조라 무작위 위치로 점프하지 못 하고 앞뒤로 움직이기만 가능하기 때문)
"..응? 쉬운데?"라는 생각이 들었다면
이진탐색을 왜 공부해야 하는지!
바로 이진탐색트리의 핵심 알고리즘이기 때문이다. (라고 생각한다.)
이진탐색트리 (BST)
1) 트리와 이진트리
트리란,
"데이터 사이의 계층 관계를 나타내는 자료구조 중 하나"이다.
일상에서도 ‘트리’를 접할 수 있다. 쉽게! (우리 노트북의 파일들도 '트리' 구조이다.)
추..가로 ‘그래프’도 있는데 ‘트리’의 부분집합이다. 사이클이 있고 없고의 차이 → 외판원순회문제 트리의 구성 요소
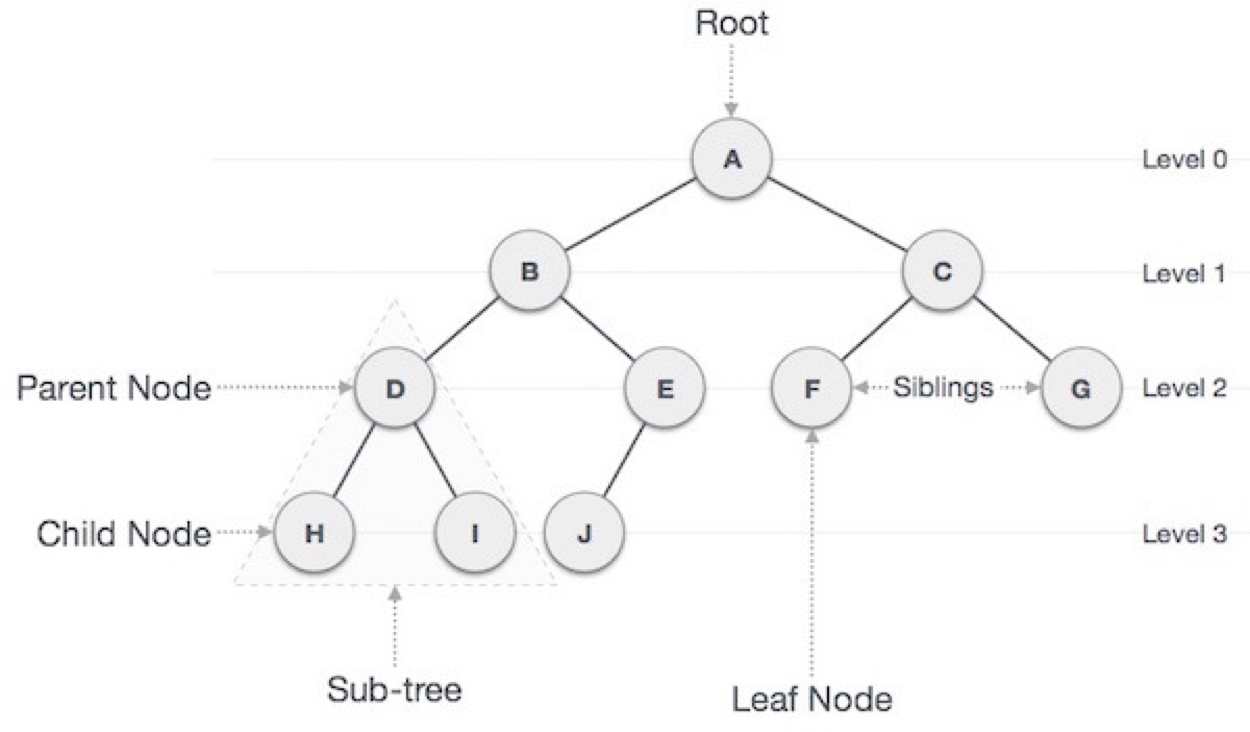
- 노드(node, vertex)와 가지(edge, branch, link, arc)
- 부모 노드 - 자식 노드 (+ 형제 노드) / root 노드 - internal 노드 - leaf 노드
- 트리의 차수 (degree)
: 트리의 최대 차수 (※ 차수 : 한 노드에 연결된 자식 노드(or 서브 트리)의 갯수) - 트리의 높이/깊이 (height/depth)
: 루트 노드부터 단말 노드까지의 경로 길이 ⇒ 최대 레벨값 + 1
▶ 즉, 이진 트리란, 자식이 최대 2명까지만! (최소 0 ~ 최대 2)
이진 트리 종류
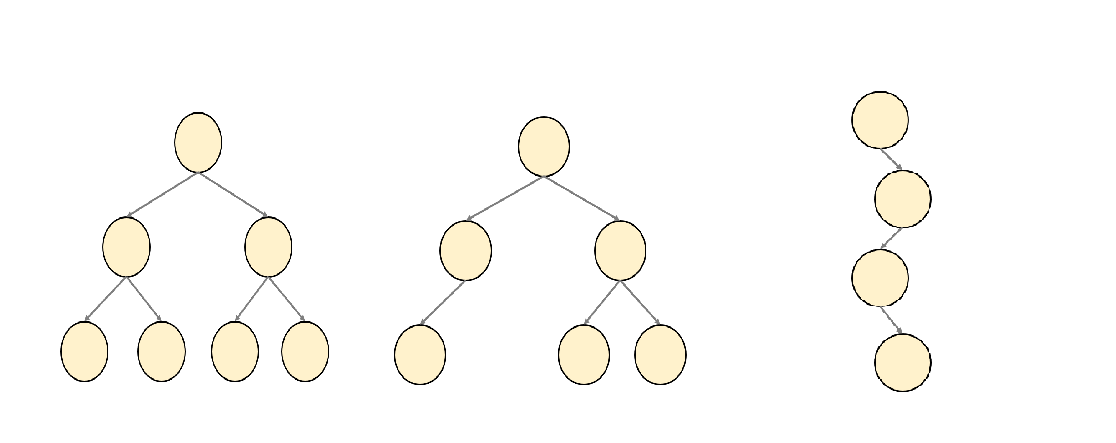
- 완전이진트리 (Complete Binary Tree)
- 모든 노드가 2개의 자식을 가진다.
- 마지막 레벨을 제외하고, 모든 레벨은 완전히 채워져 있다.
- 마지막 레벨의 모든 노드는 왼쪽부터 채워져 있다.
- 균형이진트리 (Balance Binary Tree)
- 모든 노드의 왼쪽과 오른쪽 하위 트리와의 높이가 1 이상 차이 나지 않는다.
- 변질트리 (Degenerate Tree)
- 각 부모 노드는 오직 하나의 자식 노드를 갖는다.
- 연결 리스트처럼 동작함
2) 이진탐색트리
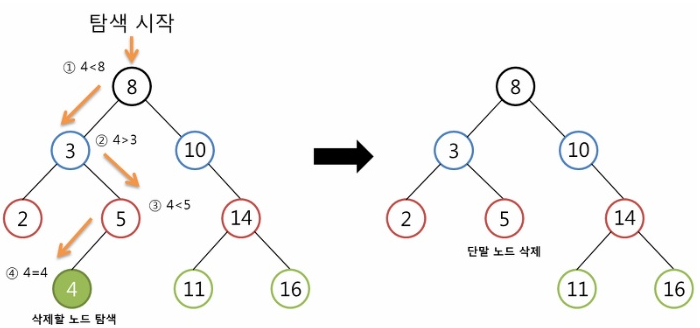
이 이상은..다음 주차 때! 커밍쑨
추가로,
파이썬에서는 찾고자 하는 원소의 인덱스를 반환하는 함수가 있다.
: obj.index(x, i, j) → 리스트 또는 튜플 obj[i:j] 안에 x와 값이 같은 원소가 있으면 그 가운데 가장 작은 인덱스를 반환한다. (없으면 예외처리로 ValueError)
[ 분할 정복 ]
“알고리즘 설계 기법 & 전략”
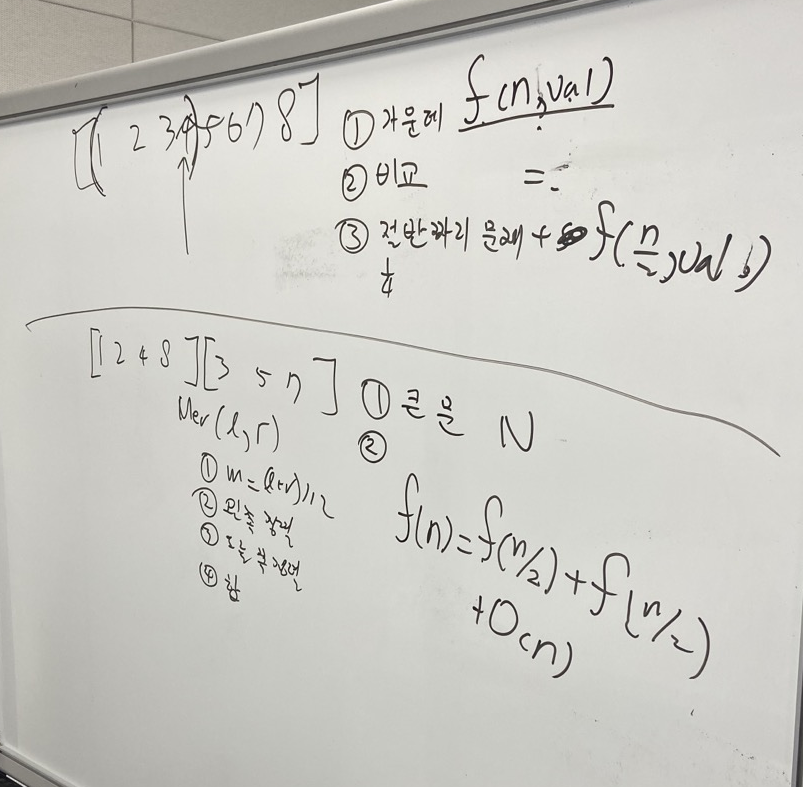이분탐색..분할정복..뭐가 뭐야?
이분탐색/분할정복 차이 (점화식을 봐보자)
- 이분 탐색은 미련이 없는 친구다.
f(n, val) = f(n/2, val)- (평균적으로) 데이터의 절반만 보고 버린다.
- 더 빨리 찾으면, 더 빨리 끝낸다.
- 분할정복은 미련쟁이 친구다.
f(n) = f(n/2) + f(n/2) + O(n)- 데이터의 절반을 보고, 또 나머지 절반도 본다.
- 결국에는 모든 데이터를 다 본다.
- 추가로, 염탐에 그치지 않고 적극적으로 대쉬한다. (데이터를 분할하고 + 재결합까지)
1. 개념
분할 정복(Divide and Conquer)은 여러 알고리즘의 기본이 되는 해결방법으로,
기본적으로는 엄청나게 크고 방대한 문제를 조금씩 조금씩 나눠가면서 용이하게 풀 수 있는 문제 단위로 나눈 다음 그것들을 다시 합쳐서 해결하자는 개념에서 출발하였다.
대표적으로는 퀵소트나 병합정렬이 있다.
(출처 : 나무위키)
“쪼개고, 합치자!”
2. 원리 (3 step)
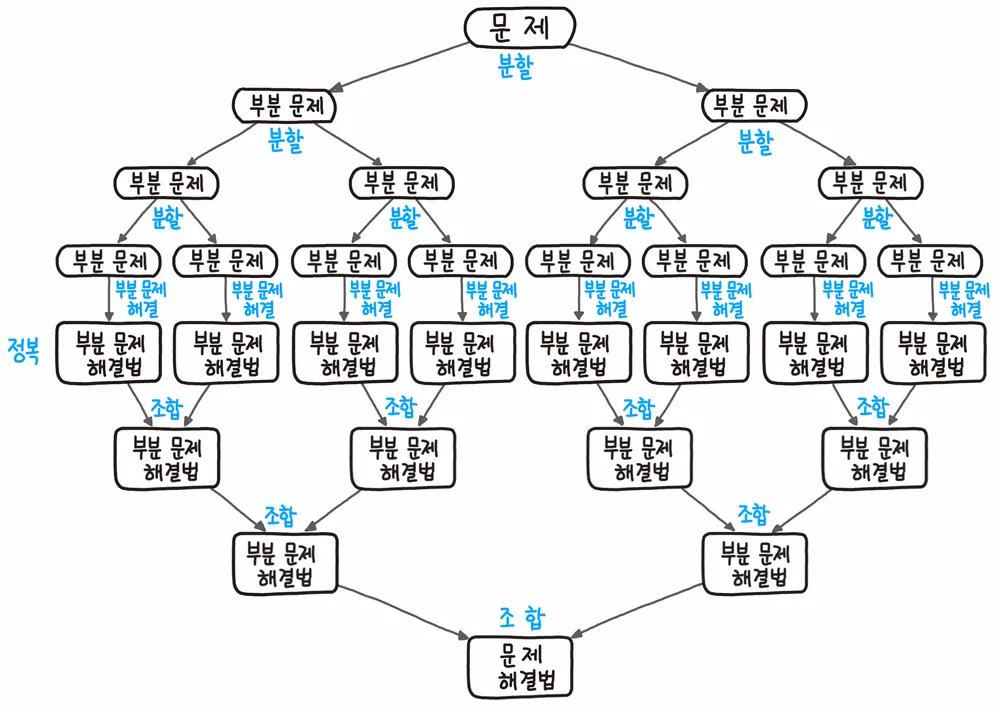
“상단에서 분할하고 중앙에서 정복하고 하단에서 조합한다.”
1) 분할 : 문제를 더이상 분할할 수 없을 때까지 동일한 유형의 여러 하위 문제로 나눈다.
2) 정복 : 가장 작은 단위의 하위 문제를 해결하여 정복한다.
3) 조합 : 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.
3. 분할정복의 프로세스 (슈도코드)
def F(x):
if F(x)가 간단 then:
return F(x)를 계산한 값
else:
x를 x1, x2로 분할
F(x1)과 F(x2)를 호출
return F(x1), F(x2)로 구한 결과값 F(x)재귀적으로 자신을 호출하면서 그 연산의 단위를 조금씩 줄여간다.
▶ 즉, “F(x)가 간단”이라는 조건을 만족할 때까지 문제를 쪼개고 쪼개서 값을 구하자!
4. 대표적인 예시
1) Merge Sort (병합 정렬)
-
Divide : 정 가운데 원소를 기준으로 재귀적으로 좌우를 분할힌다.
-
Conquer : 왼쪽의 리스트와 오른쪽의 리스트를 각각 재귀적으로 병합 정렬
-
Obtain : 정렬된 리스트를 리턴
def mergeSort(S, low, high):
if (low < high):
mid = (low + high) // 2
mergeSort(S, low, mid)
mergeSort(S, mid + 1, high)
merge2(S, low, mid, high)
def merge2(S, low, mid, high):
u = []
i = low
j = mid + 1
while (i<= mid and j <= high):
if(S[i] < S[j]):
u.append(S[i])
i += 1
else:
u.append(S[j])
j += 1
if (i <= mid):
u += S[i : mid + 1]
else:
u += S[j : high + 1]
for k in range(low, high + 1):
S[k] = u[k - low] 2) Quick Sort (퀵 정렬)
-
Divide : 기준 원소(pivot)을 정해서 기준 원소를 기준으로 좌우로 분할
-
Conquer : 왼쪽의 리스트와 오른쪽의 리스트를 각각 재귀적으로 퀵 정렬
-
Obtain : 정렬된 리스트를 리턴
def quickSort(S, low, high):
if(high > low):
pivotpoint = partition(S, low, high)
quickSort(S, low, pivotpoint - 1)
quickSort(S,pivotpoint + 1, high)
def partition (S, low, high):
pivotitem = S[low]
i = low + 1
j = high
while (i <= j):
while (S[i] < pivotitem):
i += 1
while (S[j] > pivotitem):
j -= 1
if (i < j):
S[i], S[j] = S[j], S[i]
pivotpoint = j
S[low], S[pivotpoint] = S[pivotpoint], S[low]
return pivotpoint5. 장단점 + 시간복잡도
장점
- 문제를 나눔으로써 어려운 문제를 해결할 수 있다.
(라고 한다..) - 병렬적으로 문제를 해결하는 데 큰 강점이 있다.
단점
- 재귀함수 호출로 인한 오버헤드 발생 + 스택 오버플로우 ⇒ 과도한 메모리 사용
- “F(x)가 간단”이 어떤 것이냐에 따라 알고리즘의 퍼포먼스가 생각보다 꽤 차이나게 된다.
※ 잠깐! 오버헤드란?
: 프로그램의 실행 흐름 도중 동떨어진 위치의 코드를 실행시켜야 할 때,
추가적으로 시간/메모리/자원이 사용되는 현상
(줄일 수 있는 방법 : 매크로 함수, 인라인 함수로 최적화 시킬 수 있다.)
⭐시간복잡도는 O(NlogN)
