[WEEK01] WIL 2-1. 시간/공간 복잡도

장서영·2023년 4월 12일

공간복잡도 시간복잡도 정글_WIL

정글_WIL

목록 보기

3/21

# 빅-오 # 빅-오메가 # 빅-세타

😃 참고한 글

https://velog.io/@cha-suyeon/Algorithm-시간-복잡도-공간-복잡도
https://nolzaheo.tistory.com/2

1) 개념 + 왜 알아야 할까?

시간복잡도 T(n)

알고리즘이 수행되는 데 필요한 ‘시간’ → 얼마나 빠른가?

공간복잡도

알고리즘이 수행되는 데 필요한 ‘메모리’ → 얼마나 많은 공간을 차지하는가?

▶ ‘효율성’을 위함. 더 적은 메모리를 사용하면서, 시간은 더 빠르게.

요즘, 기술 발전으로 메모리에 대한 고민이 줄어들어, 사실상 시간복잡도가 제일 관건이 됨.

▶ 시간/공간복잡도가 작다 → 빠르다. 효율적인 코드이다.

동일한 인풋과 아웃풋을 가지는 코드이더라도, 어떠한 알고리즘을 사용했느냐에 따라 시간/공간복잡도가 달라진다. 이왕이면, 용량은 적게 시간은 빠르게 하는 코드가 최고.

그리고 알고리즘은 결국, “어떤 기법을 쓰는 게 더 유용한가? (더 시간이 적게 걸리는가?)를 찾기 위함이다.” 따라서, 알고리즘을 짜고 항상 시간복잡도를 계산해야 하며, 그래서 백준에도 시간제한 + 메모리 제한이 있는 거

2) 알고리즘 분석 방법

시간복잡도

시간복잡도를 구하는 방법은,

입력 크기에 따라서 이 알고리즘의 핵심이 되는 연산(단위연산)이 몇 번 수행되는지를 결정

입력 크기 n에 대해서 “단위 연산을 몇 번 하느냐” 찾는 것 (실제 걸리는 시간 X)

step : 단위연산(핵심연산)을 결정하고 → 입력 크기 n에 대해서 몇 번 돌아가는지 검사
표현 척도 : 입력크기(n) / 단위연산 (대체로 ’비교 연산’을 사용함)
분석 방법
1) Every case : 입력 내용에 상관 없이, 입력 크기에만 좌우되는 것
▶ Every case가 안 된다면, 이제 입력 내용에 따른 케이스를 고려해 봐야 함
2) Best case : 운이 좋은 경우 → 맨 처음에 있었음. 한 번으로 끝남
3) Worst case : 운이 아주 나쁜 경우 → 맨 끝에 있거나, 없었음. n(끝까지 해야) 끝남
4) Average case : 평균

Every case가 안 된다면 → Worst case로 알고리즘을 분석 한다!

복잡도는 일반적으로 다음과 같이 나타낸다.

O(f(n)) + O(g(n)) = O(max(f(n),g(n)))

(번외) + 점근 표기법 → 왜 우리가 빅오 표현을 사용하는지?

⭐ 빅오 : 점근적 상한만 알고 있을 때 사용하는 표기법

최악의 경우에도 이 기준을 넘지 않는다. → 아무리 많이 해도 n2까지다
f(n)의 최고차항이 g(n)의 최고 차항과 같거나 작아야 한다.
즉, f(n)은 최악의 경우라도 g(n)과 같거나 빠르다.

빅오메가 : 점근적 하한만 알고 있을 때 사용하는 표기법

아무리 빨라도 이 기준보다 빠를 수 없다. → “최소 n2은 해야 한다”
f(n)의 최고차하이 g(n)의 최고차항과 같거나 커야 한다.
즉, f(n)은 최선의 경우라도 (최소) g(n)과 같거나 느리다.

빅세타 : 상한과 하한 둘 다 알고 있을 때 사용하는 표기법

딱 이 기준이다. → “딱 n2이다.”
f(n)의 최고차항이 g(n)의 최고차항과 같아야 한다.
즉, f(n)은 아무리 좋아도 나빠도 g(n)의 범위 내에 있다.

Every case가 안 된다면 Worst case를 가정해야 하기 때문에, 그래서 Big-O 표기법을 쓴다.

3) 시간복잡도 구하기

(시간복잡도의 중요성은 이 사진을 보면 확 와닿을 것이다. 입력크기가 조금이라도 커지는 순간 차이는 확이다.)

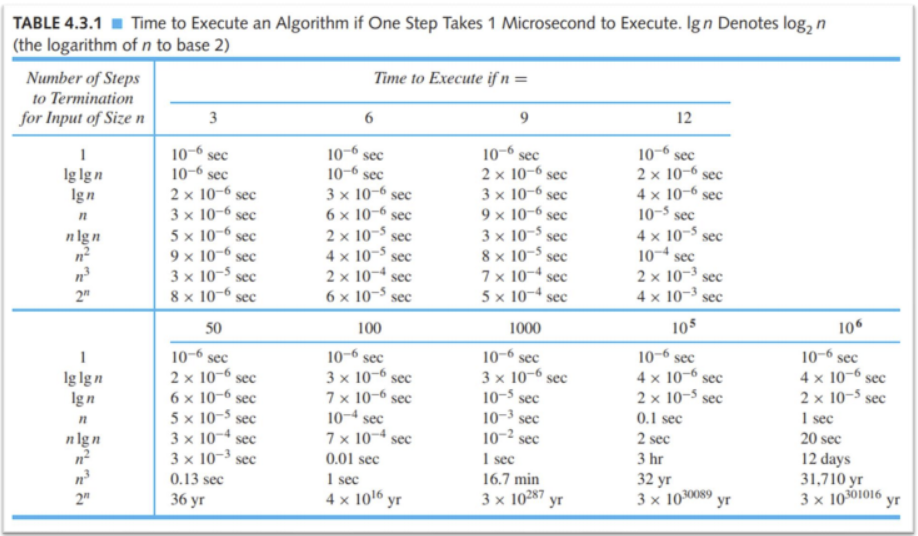
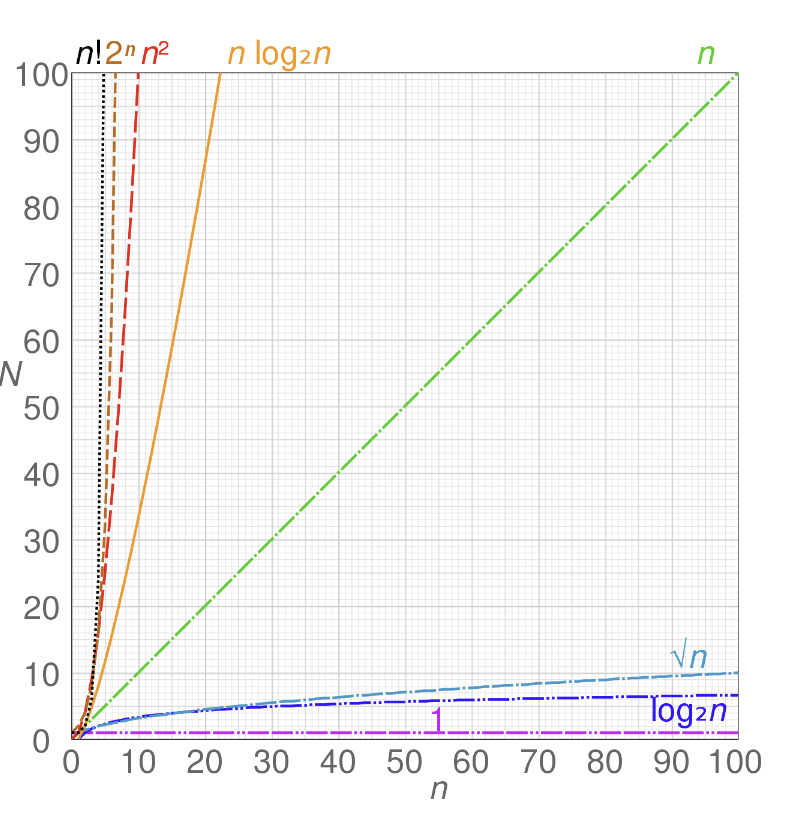
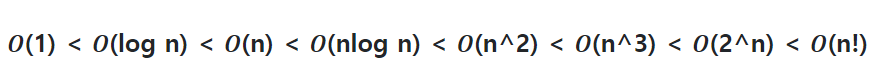
시간복잡도는 (조금 구체적으로 구하면) 다항식에서 최고차항만을 취해 계수를 지우고 빅오를 씌운다. 원칙은 그렇다.

아무튼, 선조들이 미리 정리한 시간복잡도를 유형별로 나누면,

O(1) : 입력 크기에 상관 없이 일정한 시간이 걸리는 알고리즘이다. 대표적으로, 스택의 push와 pop이 있다.

O(log n) : 입력 크기가 커질수록, 처리 시간이 로그 시간 만큼 짧아지는 알고리즘이다. (log는 2^n 지수 함수의 역함수이기 때문) 데이터가 10배 증가해도, 처리 시간은 2배만 증가한다. 대표적으로, 이진탐색에 사용된다. (재귀의 순기능에도 가능하다고 한다.)

O(n) : 입력 크기에 비례하여 처리 시간이 길어지는 알고리즘이다. 데이터가 10배 증가하면, 처리 시간도 동일하게 10배 증가한다. 대표적으로 for문(한 번)이 있다.

O(n log n) : log n과 n을 합친 것과 같다. 데이터가 10배 증가하면, 처리 시간은 20배 증가한다. 대표적으로 병합 정렬, 퀵 정렬이 이에 해당한다.

O(n^2) : 급수적으로 증가한다. 데이터가 10배 증가하면 처리 시간은 (최대) 100배가 된다. 이중 for문이 대표적이다. (만약 n m이라면 O(nm)으로 표기해야 한다!) 또한 삽입정렬, 버블정렬, 선택정렬도 이에 해당한다.

O(2^n) : 대표적으로 재귀를 통한 피보나치 수열이 있다.

O(n!) : 이 이상 말 하지 않겠다..