링크

11055 가장 큰 증가하는 부분 수열

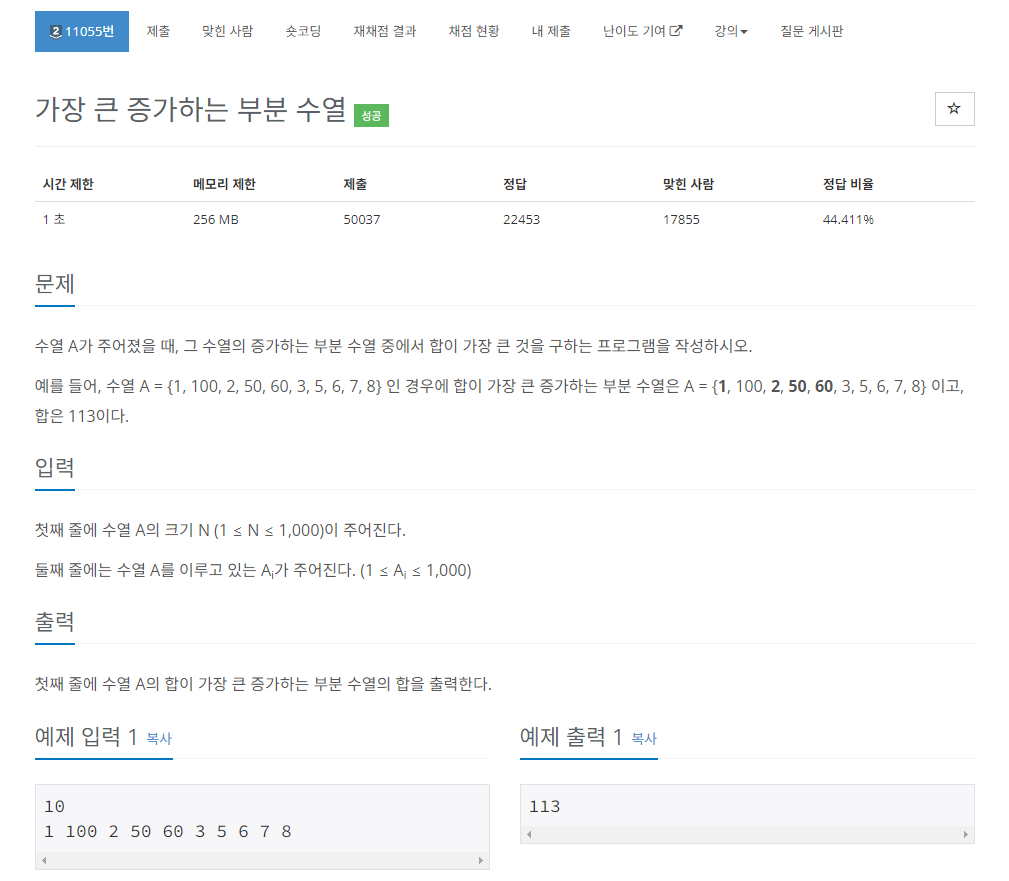
문제

풀이

이 문제는 11053 가장 긴 증가하는 부분 수열과 비슷한 문제이다(참고)

인덱스가 0부터 끝까지 반복문이 돌아가고 인덱스 전에 값들에 대해 반복문이 돌아간다.
즉 이중 반복문을 사용한다
예를들어 첫번째 반복문의 인덱스가 2라고 한다면 두번째 반복문은 0 1을 반복해야 인덱스가 2인 값과 인덱스가 0과 1일때 각각 비교해서 증가하는지 체크해야 한다

이전 문제는 길이를 묻는 것이고 이번 문제는 합이기 때문에 dp의 이전값 + 첫번째 반복문의 인덱스 값 해서 dp[i]에다가 최신화 해주면 된다.
코드를 참고하고 한번 보면 이해하기 쉬울것이다.

코드

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.*;

public class Main {

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        String[] arr = br.readLine().split(" ");

        int[] dp = new int[arr.length];
        for(int i=0;i<dp.length;i++){
            dp[i] = Integer.parseInt(arr[i]);
        }

        for(int i=0;i<arr.length;i++){

            for(int j=0;j<i;j++){

                if(Integer.parseInt(arr[i]) > Integer.parseInt(arr[j])){
                    dp[i] = Math.max(dp[i], dp[j] + Integer.parseInt(arr[i]));
                }
            }
        }

        int max = 0;
        for(int element : dp){
            max = Math.max(max, element);
        }

        System.out.println(max);
    }


}